【算法】动态规划复习汇总

一、概述

1.1 基本概念

动态规划主要用于解决多段决策最优化的问题。

动态规划通常用来解决这样的一类问题：该问题有n个输入，问题的解由这n个输入的一个子集构成，这些子集必须满足某些事先给定的约束条件，满足约束条件的子集称之为可行解。满足约束条件的可行解往往不只有一个，因此通常会给出一定的标准用来衡量可行解的优劣，这些标准称为目标函数，使得目标函数取得最大值或者最小值的可行解称之为最优解。这类问题被称之为最优化问题。

最优化问题的求解过程往往可被划分为若干个阶段，每一个阶段的决策只依赖于前一个阶段的状态，而当前决策的动作使得状态发生转移，成为下一阶段决策的依据。假设对一个状态可以做出多个决策，每一个决策可以产生一个新状态，那么动态规划的过程可以抽象为一个有向无环图结构

在多阶段决策过程中，每一个阶段的决策只和前一阶段状态有关，因此可以将每一阶段作为一个子问题来处理，然后按照问题规模的从小到大，先解决较为简单的小问题，逐渐扩大问题求解规模，直到所有问题都被求解完毕。多决断决策过程满足最优性原理，也就是各个子问题的解只和它前面的子问题的解相关，而且各个子问题的解都是相对于当前状态的最优解，整个问题的最优解是由各个子问题的最优解构成的。

1.2 设计思想

动态规划法将求解的问题划分为若干个相互重叠的子问题，每个子问题对应决策过程的一个阶段，一般来说，子问题的重叠关系是一种地推关系，将子问题的解填入一个表中，当需要求解该子问题的时候，可以直接查表获得子问题的解，从而避免了大量的重复运算。

动态规划的基本特征：

1. 最优子结构：指的是问题的最优解包含了子问题的最优解。利用最优子结构，可以自底向上地用递归逐步求出子问题的最优解，从而得到整个问题的最优解。
2. 重叠子问题：各个子问题之间并非相互独立的，而是有重叠的。而且每次产生的子问题也不总是新问题，而是已经运算过的重复问题。因此，动态规划将每个子问题的结果保存在一张表格中，使得每个子问题只需要运算一次。
3. 无后效性：即子问题的解一旦确定，就不再改变，不受在这之后、包含它的更大的问题的求解决策影响

动态规划问题的求解的三个步骤：

1. 划分子问题：将原问题分解为若干个重叠子问题，每一个子问题对应一个决策阶段。
2. 确定动态规划函数：根据子问题之间的重叠关系找到子问题满足的状态转移方程，这是动态规划的关键
3. 填写表格：设计表格，以自底向上的方式计算各个子问题的解并填表，实现动态规划过程，并且进行记忆化存储。

二、图问题中的动态规划

2.1 多段图的最短路径

设图G=(E,V)是一个带权有向图，如果把顶点集合V划分成k个不相关的子集Vi，使得E中的任意一条边都满足u属于V_i，v属于V_i+m，那么可以称图G为多段图，多段图最短路径问题就是求从源点到终点的最短路径。

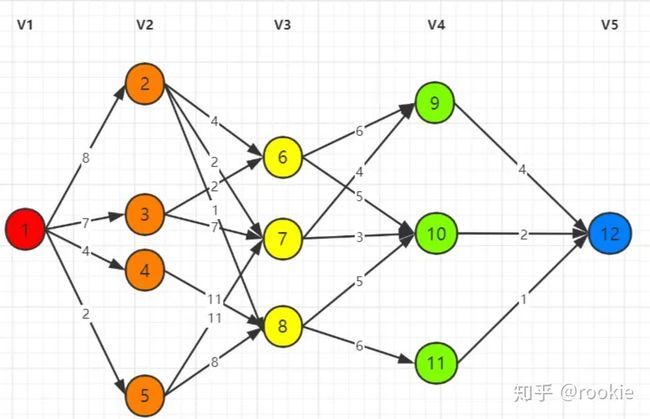
求解思想
多段图最短路径问题是满足最优性原理

首先划分子问题：由于多段图被划分为k个不相交的子集Vi，求解子集Vi的中各个顶点的最短路径就是一个子问题，而且是一个重叠子问题，因为求解子集Vi中的某一顶点的最短路径，需要遍历该顶点所有的入边，然后将这些入边的权值加上其出弧头结点的最短路径得出各个边到当前顶点的最短路径。而弧头结点位于的子集Vj一定位于Vi之前。也就是子集Vi的求解依赖于在它之前的子集的求解，基于前面子集的解得出Vi的解。

接下来是确定动态规划函数，又称为状态转移函数。而它的状态转移方程就是，设有一个弧从节点u指向节点v，源点s到结点v的最短路径等于源点s到各个结点u的最短路径加上节点u到节点v的边的权，然后从这些可行解中选出路径最小的最优解。

接下来就是填写表格，将最优解填入表格中，供后续的求解使用。

2.2 多源点最短路径

问题：
给定带权图G=(V,E)，对于任意顶点vi和vj，求顶点vi到vj的最短路径长度。

想法：
对于该算法，需要两个n*n的辅助数组：其中数组A用于存储各个顶点到各个顶点目前的最短距离，path数组用于存储两个顶点之间最短路径的中转点。该问题的子问题是：两个顶点在允许经过一个顶点集合V的情况下，他们的最短距离是多少。初始子问题是，A数组中存储着不经过任何顶点中转，各个顶点到各个顶点的最短距离，实际上就是顶点之间直接相连的边中权值最小的边；接着我们考虑允许经过V0顶点，各个顶点到各个顶点的最短距离，状态转移方程也很简单：求允许经过V0顶点下，V1到V2的最短距离，那么只需要看是V1直接到V2的距离比较短，还是V1经过V0到V2的距离比较短，将距离较短者更新到A矩阵和path矩阵就好。以此类推，接下来考虑允许经过V0或V1顶点，各个顶点到各个顶点的最短距离，那么我们只需要在先前的基础上考虑经过V1顶点的情况，因为经过V0顶点的情况已经存储在了矩阵中，这就是动态规划的重叠子问题和记忆化存储：上一个子问题的状态是当前规模更大的子问题的一部分，而上一个子问题得出的解为解决当前子问题提供了部分解。接下来重复上述步骤，经过n轮递推之后，最终求出各个顶点之间的最短路径。

2.3 TSP问题

需要提示的是，本文中TSP主要着重于在面试时被问到了该如何口述，如果需要详细论证或者入门学习的，请移步其他文章
问题：
TSP问题是指旅行家要旅行n个城市，要求各个城市经历并且只经历一次然后回到出发城市，并且要求所走的路径最短。

想法：
首先判断问题的最优子结构，如果从节点c1出发经过c2,c3,c4…cn再回到c1的最短环路序列为{c1,c2,c3…cn,c1}，那么其子序列，也就是{c1,c2,…ci}（in-1也就是当前子问题的求解依赖于上一个子问题的解。

设i为起始顶点，d{k,C}表示从顶点k，经过集合C中的所有城市后，回到起始顶点的最短路径。

口述：
首先判断问题的最优子结构，如果存在一个最优序列，使得从起始顶点a出发经过序列上的城市后再回到a的路径最短，那么该序列的子序列，也就是经过若干城市后回到起始顶点a，它的路径也是最短的。就可以通过求解其较小的子序列作为最优子结构，逐步求出最短环路。不难看出，该子问题也是重叠的，比如要求解c1经过n个城市的最短路径，那么必须求解出c1经过n-1个城市的最短路径d_n-1也就是当前子问题的求解依赖于上一个子问题的解。

那么什么是它的初始子问题呢？那就是只经过一个城市后回到起始顶点的路径是多少，此时可以得出n-1个可行解。接下来，基于该子问题，可以得经过2个城市后回到起始顶点的可行的序列以及他们路径长度，以此类推，直到求解到经过n-1个城市后回到起始城市的各个可行序列以及他们的路径长度。此时只差最后一步，将路径序列构成一个回路，设序列s为从c1出发经过n-1个城市到达起始顶点a，那么我们只需要将从起始顶点a到c1的路径长度加上序列s的路径长度，就可以得到回路的路径长度。最后我们会得到n-1个回路序列，选出其中路径长度最小的回路，就是最优解。而最优回路可以直接通过回溯得到。

三、组合问题的动态规划

3.1 最长递增子序列问题

描述：
在数字序列A={a1, a2, …an}中按照递增的下标序列选出一个子序列B={b1,b2,…bk}，如果子序列B中数字都是严格递增的，那么就称子序列B为序列A的递增子序列。最长递增子序列问题，就是要找出序列A中最长的一个递增子序列。比如数字序列{5,2,8,6,3,6,9,7}的最长递增子序列为{2,3,6,9}

思路：
首先我们来划分子问题，设L(n)为序列A={a1,a2,…, an}的最长递增子序列的长度，那么可以先求解他的子问题L(i)也就是序列A的子序列{a1,a2…ai}的最长递增子序列B的长度。显然，初始子问题是求L(1)，也就是只有一个元素的子序列{a1}的最长递增子序列，显然L(1)=1。接下来开始通过状态转移方程逐步求解重叠子问题，这需要一个长度为n的数组dp用于存储L(i)的值，也就是下标i存储的值为前i个元素的最长递增子序列。假设我们要求解前i个元素的最长递增子序列，那么此时前i-1个元素的递增子序列已经求解出来并且存储到数组p中的，此时我们不需要重头遍历，而是用第i个元素和前i-1个元素对比，如果第i个元素大于前i-1中的某个元素，那么第i个元素可以加入到该元素的最长递增子序列中，也就是dp[i]=dp[j]+1。这样可以找出所有的递增子序列，也就是动态规划中的可行解，从所有可行的递增子序列中选出最长的递增子序列，填入到dp[i]中，得出前i个元素的最长递增子序列。但是也有特殊情况，如果前i-1个元素都比第i个大，那么意味着最长递增子序列只有A[i]本身，即dp[i]=1。以此类推，将i=1一直推广到i=n，那么最长递增子序列就求出来了。

开销：
对于前i个元素的最长递增子序列的查找需要遍历前i个元素，因此时间复杂度为O(n^2)

3.2 最长公共子序列

问题：
对于给定序列X={x1,x2,…xm}和序列Z={z1,z2,…zk}，假设X={a,b,c,d,a,b}，Z={b,c,d,b}，那么可以称Z为X的公共子序列。给定两个序列X和Y，如果序列Z即是X的子序列又是Y的子序列，那么称Z为公共子序列。那么最长公共子序列问题就是需要在X和Y之间寻找最长的公共子序列。

思想：
X和Y两个序列的最长公共子序列包含了这两个序列的前缀序列的最长公共子序列，因此最长公共子序列问题满足最优性原理。接下来我们划分下子问题，设L(m,n)表示长度分别为m和n的序列X和Y的最长公共子序列。那么子问题就是L(i,j)表示序列X的前i个元素和序列Y的前j个元素的最长公共子序列。那么初始子问题是序列X和序列Y其中一个是空序列，也就是L(0,j)和L(i,0)都为0。

接下来我们讨论他们的状态转移方程，假设Z为L(i,j)的公共子序列，如果xi=yj=zk，也就是意味着Z_k-1是X_i-1和Y_j-1的最长公共子序列。如果$xi\ne yj$，并且$zk\ne yj$，则Z_k是X_i和Y_j-1的最长公共子序列。如果$xi\ne yj$，并且$zk\ne xi$，则Z_k是X_i-1和Y_j的最长公共子序列。

也就是当我们要求解L(i,j)的时候，如果xi=yj，那么可以找出X_i-1和Y_j-1的最长公共子序列，然后在该子序列后面加上xi就可以得出Xi和Yi的最长公共子序列；如果KaTeX parse error: Undefined control sequence: \neqyj at position 3: xi\̲n̲e̲q̲y̲j̲，则需要求解两个子问题：找出X_i-1和Y_j的最长公共子序列和X_i和Y_j-1的最长公共子序列，这两个子序列中的较大者就是Xi和Yi的最长公共子序列。最终会将问题分解为初始子问题，分解到初始子问题后，再将他们进行回溯，就可以得到最长公共子序列。

开销：
在该算法中，首先需要使用用两个分别为n次和m次的for循环，接着是一个两层嵌套的，mxn的for循环，因此时间复杂度为O(n*m)

3.2 0-1背包问题

问题描述：
给定n种物品和一个背包，物品i的重量为w_i，其价值为v_i，背包容量为C，如何选入装入背包的物品，使得装入背包中物品的总价值最大？

分析：
首先我们需要定义子问题，0-1背包问题可以看做决策一个含有n个变量的序列，对第i个变量根据一定条件赋以1或0值。0-1背包问题的子问题可以看做是允许将前i个物品放入容量为j的背包中的最大价值，注意，是允许将前i个物品放入背包，而不是将前i个物品全部放入背包。显然，该问题的初始子问题是将0个物品放入容量为j的背包中（KaTeX parse error: Undefined control sequence: \leqC at position 8: 0\leq j\̲l̲e̲q̲C̲)和允许将前i个物品装入容量为0的背包中，显然，这两种情况背包的价值都是0，因为实际上容量为0的背包装不下任何物品，而不装物品的背包无论容量多少价值也是0的。

接着我们开始分析状态转移方程：设需要求解子问题，允许将前i件物品放入容量为j的背包中可以获得的最大价值，那么对于第i件物品，有两种情况：第一种情况是将第i件物品不装入背包，那么实际上允许装入前i个物品实际上是和允许装入前i-1件物品的最大价值是一样的；如果装入该物品，那么背包的容量就还剩下了j-wi，此时背包的最大价值等于允许将前i-1个物品装入容量为j-wi的背包的最大价值加上vi。我们对比这两种情况。然后选择价值更大者作为该子问题的解。这种方式将允许前i件物品装入背包的子问题转化为了允许将前i-1个物品装入背包和允许将前i-1个物品装入容量为j-wi的背包的求解，最终会转化为对初始子问题的求解。然后通过回溯可以求得各个子问的最优解，最终得到问题的最终答案。

时间开销：
第一个for循环时间性能是O(n)，第二个for循环为O©，这两个for循环用于求解初始子问题。接下来是一个nxC的二层循环，时间复杂度为O(nxC)，因此整个算法的时间复杂度为O(nxC)

四 、查找问题中的动态规划

4.1 最优二叉查找树

设{r1,r2,r3…rn}是n个记录的集合，其查找概率分别是{p1,p2…pn}，求这n个记录构成的最优二叉查找树。最优二叉查找树是以这n个记录构成的二叉查找树中具有最少平均比较次数的二叉查找树。

4.2 近似串匹配问题

问题：
在一个文本中查找某个给定单词，由于单词本身可能有文法上的变化，加上书写和印刷上的错误，实际上往往需要进行近似串匹配。设样本P=p₁p₂…p_m，文本为T=t₁t₂…t_n，有一个负整数K，规定样本P和实际的文本T之间包含有最多不少过K个差别，这里的差别指的是以下三种情况：

• 修改：P和T对应的字符不同
• 删去：T中含有一个未在P中出现的字符
• 插入：T中不含有P中出现的一个字符
  这类问题被称之为样本P和文本T的K-近似值匹配问题，其中K包含两种意思：1.二者差别最多为K 2.差别数是指二者在所有匹配对应方式下的最小编辑错误总数