APPNP

Paper : Predict then Propagate: Graph Neural Networks meet Personalized PageRank
Code : official

摘要

随着GNN网络层数的提高，存在过平滑和参数量过大难以训练的问题。作者探索了GCN与PageRank算法之间的关系，提出了基于Personalized Page Rank 的改进版本的信息传递方式PPNP(Personalized Propagation of Neural Prediction)，以及快速近似版本APPNP。引入APPNP的模型可以大幅减少参数量，并取得较好的效果。Personalized Page Rank 增加了跳转回根节点的机会，因此可以平衡保留local信息和利用大范围邻居信息。作者还将MPNN结构中的消息传递分离出来，为每个点提供了一个较大的感受野的同时不引入参数。

Page Rank & Personalized Page Rank

Page Rank 算法是Google创始人Larry Page 提出的，使用网络超链接进行网页重要性得分的计算算法。Page Rank的初始想法源自论文的引用，如果某篇论文被一篇非常重要的论文所引用，那么该篇论文的重要性也比较高，因为它被重要的论文背书了。一个基本的想法是某论文的重要性得分源自所有引用它的论文，而该论文又对所有它引用的论文进行重要性评估。回到互联网上的超链，Larry Page认为，重要性可以看作是某人在某个节点上以等概率跳转到该节点引用的节点，而重要性描述了最终停在每个节点上的概率。形式化的表示为

$$\text{PR}(v)=\sum _{(u,v)\in E}\frac{\text{PR}(u)}{d_{\text{out}}(u)}$$

而Page Rank 是通过随机游走的方法对得分进行迭代式计算，假定存在引用图

转移矩阵定义为

$$T=\left[\begin{array}{cccc}0& \frac{1}{2}& 1& 0\\ \frac{1}{3}& 0& 0& \frac{1}{2}\\ \frac{1}{3}& 0& 0& \frac{1}{2}\\ \frac{1}{3}& \frac{1}{2}& 0& 0\end{array}\right]$$

初始时，所有点的重要性相同，设为

$$w_0=\left[\begin{array}{c}\frac{1}{4}\\ \frac{1}{4}\\ \frac{1}{4}\\ \frac{1}{4}\end{array}\right]$$

因此，对每个点随机游走一次后，结果表示为

$$w_1=T{w}_0$$

迭代n次后的结果即为最终的节点重要性。

但是，以上的过程中存在两个问题：

• 等级泄露：某点没有出度，那么最终收敛时，该节点的重要性为1
• 等级沉默：某点没有入度，那么最终收敛时，该节点的重要性为0

为了解决该问题，Page Rank 假定网页上存在一个随机跳转按钮，点击后可以随机跳转到任意一个网页上，当，因此，Page Rank 得分形式化表示为

$$\text{PR}(v)=\mu \frac{1}{N}+（1-\mu ）\sum _{(u,v)\in E}\frac{\text{PR}(u)}{d_{\text{out}}(u)}$$

其中 $\mu$ 描述不根据超链进行跳转的概率。使用矩阵描述以上的表达式，即为

$$w=(1-\mu )Tw+\mu e$$

其中 $e$ 表示全为 $\frac{1}{N}$ 的向量。

Personalized Page Rank算法继承了经典PageRank算法的思想，利用图链接结构来递归地计算各结点的权重，即模拟用户通过点击链接随机访问图中结点的行为 计算稳定状态下各结点得到的随机访问概率。PPR与Page Rank的最大区别在于随机行走中的跳转行为。为了保证随机行走中各结点的访问概率能够反映出用户的偏好，PPR算法要求在随机行走中的每次跳转不可随机选择到任意结点，用户只能跳转到一些特定的结点，即代表用户偏好的那些结点。因此，在稳定状态下，用户所偏好的那些结点和相关的结点总能够获得较高的访问概率。PPR算法表示为：

$$w=(1-\mu )Tw+\mu v$$

其中 $|v|=1$ 表示用户的偏好。

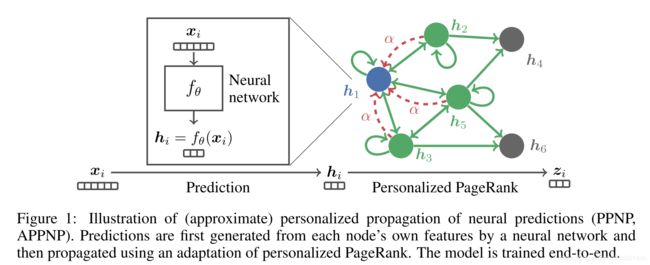
PPNP

Page Rank 算法采用的正则邻接矩阵定义为
$$A_{rw}=A{D}^{-1}$$

作者使用GCN中的邻接矩阵$\overline{A}=D^{-1/2}A{D}^{-1/2}$ 代替正则邻接矩阵，假定使用one-hot 向量 $i_x$ 指示根节点，有

$$\begin{gathered} {\pi }_{ppr}(i_x)=(1-\alpha )\overline{A}{\pi }_{ppr}(i_x)+\alpha i_x \\ {\pi }_{ppr}(i_x)=\alpha (I_n-(1-\alpha )\overline{A}{)}^{-1}{i}_x \end{gathered}$$

将该等式应用到PPNP中，表示对图数据进行数据聚合，模型等式为

$$\begin{gathered} {Z}_{\text{PPNP}}=\text{softmax}(\alpha (I_n-(1-\alpha )\overline{A}{)}^{-1}H) \\ \text{where }H=f_{\theta }(X) \end{gathered}$$

其中 $X$ 表示点特征矩阵，$f_{\theta }$ 表示一个神经网络，从特征映射到预测结果。简单来说，PPNP将预测/特征空间映射和信息聚合进行分离，在数据聚合的过程中除了$\alpha$没有引入任何参数，因此避免了参数爆炸的问题。

APPNP

为了加快计算的速度，作者采用近似的方法来避免计算矩阵的逆，即

$$\begin{gathered} {Z}^{(0)}=H=f_{\theta }(X) \\ {Z}^{k+1}=(1-\alpha )\overline{A}{Z}^{(k)}+\alpha Hk\in [0,K-2] \\ {Z}^{(K)}=\text{softmax}((1-\alpha )\overline{A}{Z}^{K-1}+\alpha H) \end{gathered}$$

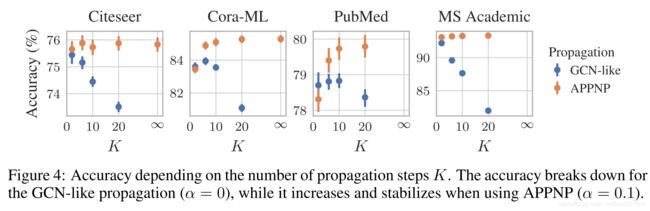
作者通过实验证明了APPNP在层数趋于无穷时，表达式等价于PPNP算法。注意在迭代式中加入非线性层效果会更好，这个结果比较直观，因为更多的非线性层的引入可以增强模型的表示能力。

实验结果

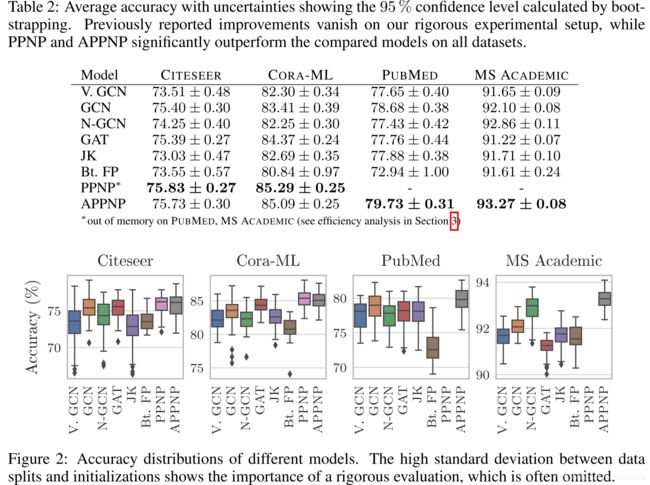
实验结果表明APPNP具有较好的表现和较低的方差，鲁棒性较好。

表格3体现出APPNP具有较好的训练速度。

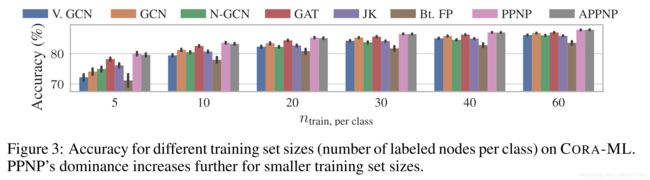
图表3体现出PPNP和APPNP在节点标签较少时，具有良好的表现。

图表4体现APPNP对过拟合的缓解能力。

图表5展示了算法对 $\alpha$ 的敏感程度

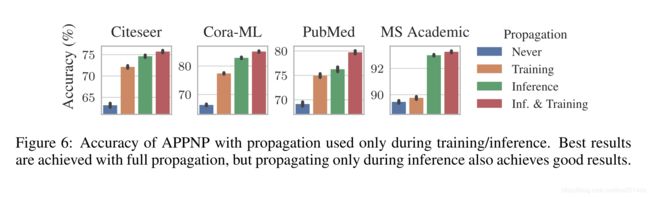
消融实验结果如下所示

总结

作者使用了一种简单的方法，将GCN中的预测和传播解耦，并解决了许多消息传递模型固有的有限范围问题，而无需引入任何其他参数。它使用来自一个较大的，可调整的邻域的信息对每个节点进行分类，并且具有较高的计算效率，其性能优于几种针对图进行半监督分类的方法。个人认为在学术引用的数据集上有效不一定在其它数据集也有效，相对来说论文引用任务比较简单，如果变成分子数据集或是其他的数据集效果就不一定了。而且最有意思的PPNP是直接对预测进行加减的聚合操作，不一定所有的预测向量都是可加的。