搜索与图论 - 搜索与图在算法中的应用【上】
目录
DFS
排列数字
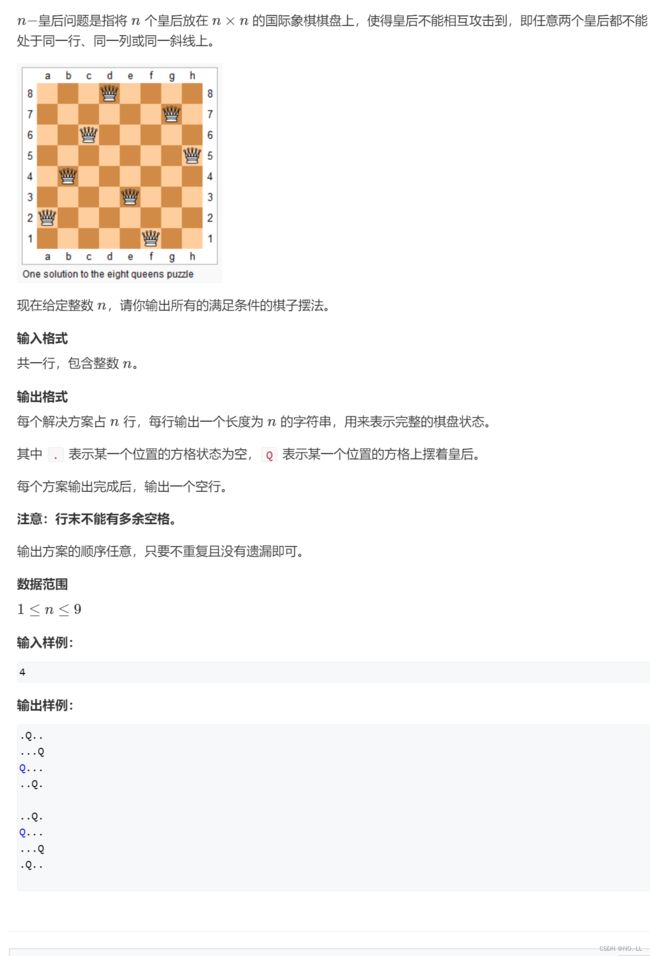
n-皇后问题
BFS
走迷宫
八数码
树与图的深度优先遍历
数的重心
树与图的广度优先遍历
图中点的层次
拓扑排序
有向图的拓扑序列
DFS
排列数字
![]()
#include
using namespace std;
const int N=10;
int n;
int path[N];
bool st[N];
void dfs(int u)
{
if(u==n)
{
for(int i=0;i>n;
dfs(0);
return 0;
} n-皇后问题
思路:
按行枚举 时间复杂度O(n*!n)
难点:如果判断是否在同一条斜线
因为斜线斜率相同,所以唯一区分就是截距,截距相同则是同一条斜线
截距表示方法:
下面分析中的(x,y)相当于上面的(u,i)
- 反对角线 y=x+b 截距 b=y−x,因为我们要把 b 当做数组下标来用,显然 b 不能是负的,所以我们加上 +n (实际上+n+4,+2n都行),来保证是结果是正的,即 y - x + n
- 正对角线 y=−x+b, 截距是 b=y+x,这里截距一定是正的,所以不需要加偏移量
注意:列col必须由 i 表示,因为后面会一直递归是由dfs(u+1)推进的,若由 u 表示则造成第一行相同的情况;
也就是说 col,dg,udg保证列、对角线、反对角线上无重复元素,而col固定保证列不重时再由u+1推进才能保证行不重
#include
using namespace std;
const int N = 20;
// bool数组用来判断搜索的下一个位置是否可行
// col列,dg对角线,udg反对角线
// g[N][N]用来存路径
int n;
char g[N][N];
bool col[N], dg[N], udg[N];
void dfs(int u) {
// u == n 表示已经搜了n行,故输出这条路径
if (u == n) {
for (int i = 0; i < n; i ++ ) puts(g[i]); // 等价于cout << g[i] << endl;
puts("");
return;
}
//对n个位置按行搜索
for (int i = 0; i < n; i ++ )
// 剪枝(对于不满足要求的点,不再继续往下搜索)
// udg[n - u + i],+n是为了保证下标非负
if (!col[i] && !dg[u + i] && !udg[n - u + i]) {
g[u][i] = 'Q';
col[i] = dg[u + i] = udg[n - u + i] = true;
dfs(u + 1);
col[i] = dg[u + i] = udg[n - u + i] = false; // 回溯,还原使用前所有情况
g[u][i] = '.';
}
}
int main() {
cin >> n;
for (int i = 0; i < n; i ++ )
for (int j = 0; j < n; j ++ )
g[i][j] = '.';
dfs(0);
return 0;
}
BFS
走迷宫
思路:
记忆:
初始化队头、距离数组、四个方向
从初始化点开始遍历,符合条件的点都入队
数组模拟队列
#include
#include
#include
using namespace std;
const int N = 110;
typedef pair PII;
int n, m;
int g[N][N];//存放地图
int d[N][N];//存 每一个点到起点的距离
PII q[N * N];//手写队列 地图有N*N个点
int bfs()
{
int hh = 0, tt = 0;
q[0] = {0, 0};
memset(d, - 1, sizeof d);//距离初始化为- 1表示没有走过
d[0][0] = 0;//表示起点走过了
int dx[4] = {-1, 0, 1, 0}, dy[4] = {0, 1, 0, -1};//x 方向的向量和 y 方向的向量组成的上、右、下、左
while(hh <= tt)//队列不空
{
PII t = q[hh ++ ];//取队头元素,hh++相当于头删q.pop();
for(int i = 0; i < 4; i ++ )//枚举4个方向
{
int x = t.first + dx[i], y = t.second + dy[i];//x表示沿着此方向走会走到哪个点
if(x >= 0 && x < n && y >= 0 && y < m && g[x][y] == 0 && d[x][y] == -1)//在边界内 并且是空地可以走 且之前没有走过
{
d[x][y] = d[t.first][t.second] + 1; //到起点的距离+1
q[ ++ tt ] = {x, y};//新坐标入队
}
}
}
return d[n - 1][m - 1]; //输出右下角点距起点的距离即可
}
int main()
{
cin >> n >> m;
for(int i = 0; i < n; i ++ )
for(int j = 0; j < m; j ++ )
cin >> g[i][j];
cout << bfs() << endl;
return 0;
}
C++ queue
#include
#include
#include
using namespace std;
const int N = 110;
typedef pair PII;
int n, m;
int g[N][N], d[N][N];
int bfs()
{
queue< pair > q;
q.push({0, 0});
memset(d, -1, sizeof(d));
d[0][0] = 0;
int dx[4] = {-1, 0, 1, 0}, dy[4] = {0, 1, 0, -1};
while (q.size())//队列不为空
{
PII t = q.front();//取队头元素
q.pop();//出队
for (int i = 0; i < 4; i++)
{
int x = t.first + dx[i], y = t.second + dy[i];
if (x >= 0 && x < n && y >= 0 && y < m && g[x][y] == 0 && d[x][y] == -1)
{
d[x][y] = d[t.first][t.second] + 1;//当前点到起点的距离
q.push({x, y});//将新坐标入队
}
}
}
return d[n - 1][m -1];
}
int main()
{
cin >> n >> m;
for (int i = 0; i < n; i++)
for (int j = 0; j < m; j++)
cin >> g[i][j];
cout << bfs() << endl;
return 0;
}
补充:打印路径
因为Prve存的是该路径的上一步操作
#include
#include
#include
using namespace std;
const int N = 110;
typedef pair PII;
PII q[N*N],Prev[N][N];
int g[N][N], d[N][N];
int n, m;
int bfs()
{
int hh = 0, tt = 0;
q[0] = {0, 0};
memset(d, -1, sizeof d);
int dx[4] = {-1, 0, 1, 0}, dy[4] = {0, 1, 0, -1};
d[0][0] = 0;
while(hh <= tt)
{
PII t = q[hh ++ ];
for(int i = 0; i < 4; i ++ )
{
int x = dx[i] + t.first, y = t.second + dy[i];
if(x >= 0 && x < n && y >= 0 && y < m && g[x][y] == 0 && d[x][y] == -1)
{
d[x][y] = d[t.first][t.second] + 1;
Prev[x][y] = t;
q[++ tt] = {x, y};
}
}
}
int x = n - 1, y = m - 1;
while(x || y)//有一个不d等于0
{
cout << x << ' ' << y << endl;
PII t = Prev[x][y];
x = t.first, y = t.second;
}
return d[n - 1][m - 1];
}
int main()
{
cin >> n >> m;
for(int i = 0; i < n; i ++ )
for(int j = 0; j < m;j ++)
cin >> g[i][j];
cout << bfs() << endl;
return 0;
}
八数码
思路:
用map
#include
#include
#include
#include
using namespace std;
int bfs(string start)
{
string end="12345678x";//最终完成的状态
queue q;
unordered_map d;//利用字符串记录距离
q.push(start);
d[start]=0;
int dx[4]={0,0,-1,1},dy[4]={1,-1,0,0};
while(q.size())
{
auto t=q.front();
q.pop();
int distance=d[t];
if(t==end) return distance;
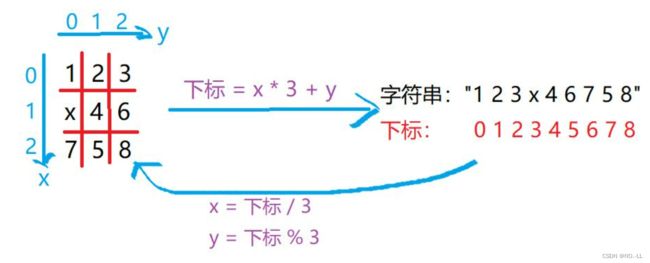
int k=t.find('x'); //一维下标转换为二维坐标
int x=k/3,y=k%3;
for(int i=0;i<4;i++)
{
int a=x+dx[i],b=y+dy[i];//(a,b)表示移动后x坐标
if(a>=0&&a<3&&b>=0&&b<3)
{
swap(t[k],t[3*a+b]);
//当前状态是第一次遍历,记录距离,入队
if(!d.count(t))
{
d[t]=distance+1;
q.push(t);
}
//还原状态,为下一状态准备,因为该状态有4种走法
swap(t[k],t[3*a+b]);
}
}
}
return -1;
}
int main()
{
string c,start;
for(int i=0;i<9;i++)
{
cin>>c;
start+=c;
}
cout< 树与图的深度优先遍历
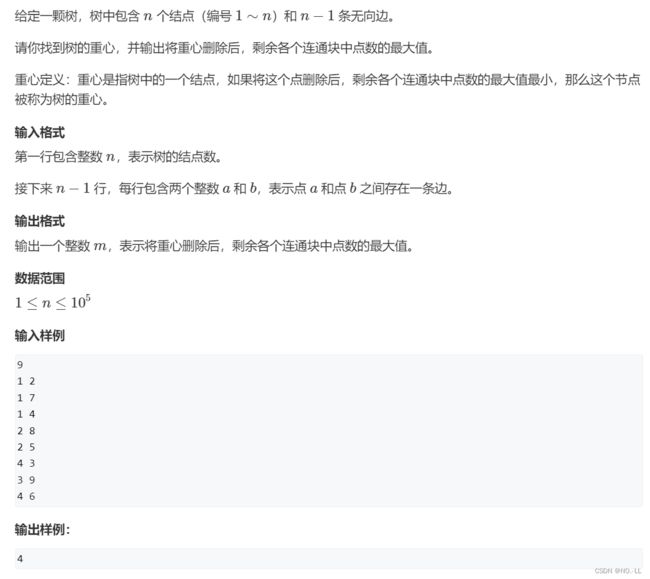
数的重心
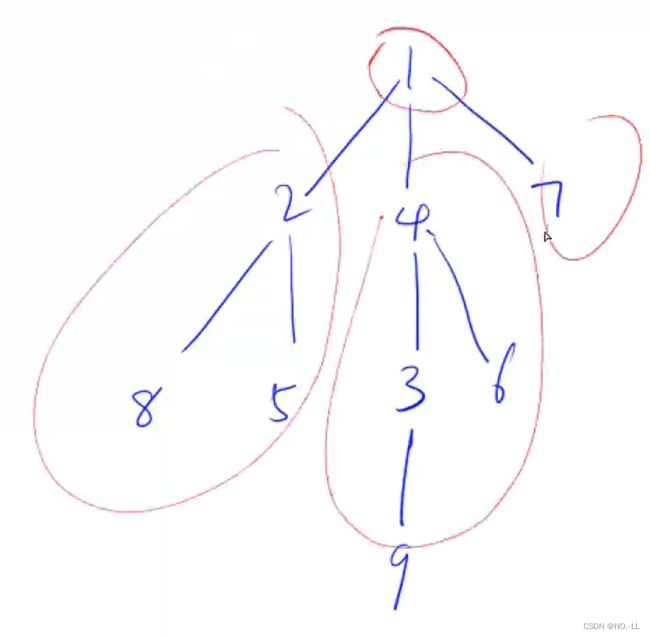
1、由题意画图得:如图删除1节点,连通快最大值为4,是所有连通块最大值中最小的
2、存储无向图我们可以看成特殊的有向图,即让每个节点都双向连接;
存储有向图我们用邻接表存储
void add(int a,int x) { e[idx]=x,ne[idx]=h[a],h[a]=idx++; }该操作表示以节点a为头,头插插入入一个为x的结点
3、如何遍历树?
树的dfs模板
// 需要标记数组st[N], 遍历节点的每个相邻的便 void dfs(int u) { st[u] = true; // 标记一下,记录为已经被搜索过了,下面进行搜索过程 for (int i = h[u]; i != -1; i = ne[i]) { int j = e[i]; if (!st[j]) { dfs(j); } } }
4、如何求最大连通子图
如图所示,假设节点4为树的重心,那么可以通过dfs(4)来遍历以4为根的子树,求该树得节点数;然后我们可以惊奇的发现,除了该子树以外,其他节点必构成连通子图,那么连通子图值就为n-size4
对于树中的连通子图,利用dfs不断更新取最大值;
int dfs(int u) { int res=0;//存储删除某节点后 最大连通子图值 st[u]=true;//表示u节点已经访问过 int sum=1;//以u为根的树的节点数(包括u) //访问u的每个子节点 for(int i=h[u];i!=-1;i=ne[i]) { int point=e[i]; if(!st[point])//若该节点没访问过 { int s=dfs(point);// u节点的单颗子树节点数 res=max(res,s);//记录最大连通子图 sum+=s;//以point为根的树 的节点数 } } res=max(res,n-sum); return sum; }
本题的本质是树的dfs,每次dfs可以确定以u为重心的最大连通块的节点数,并且更新一下ans。
也就是说,dfs并不直接返回答案,而是在每次更新中迭代一次答案。
这样的套路会经常用到,在 树的dfs 题目中
#include
#include
#include
using namespace std;
const int N=1e5+10;
const int M=2*N;
int h[N],e[M],ne[M],idx,n;
int ans=N;
bool st[N];
void add(int a,int x)//只是用于存储节点和指向的工具,idx与节点数值point无关
{
e[idx]=x,ne[idx]=h[a],h[a]=idx++;
}
int dfs(int u)
{
int res=0;//存储删除某节点后 最大连通子图值
st[u]=true;//表示u节点已经访问过
int sum=1;//以u为根的树的节点数(包括u)
//访问u的每个子节点
for(int i=h[u];i!=-1;i=ne[i])
{
int point=e[i];
if(!st[point])//若该节点没访问过
{
int s=dfs(point);// u节点的单颗子树节点数
res=max(res,s);//记录最大连通子图
sum+=s;//以point为根的树 的节点数
}
}
res=max(res,n-sum);
ans=min(ans,res);//遍历过的假设重心中,最小的最大联通子图的 节点数
return sum;
}
int main()
{
memset(h,-1,sizeof h);
cin>>n;
for(int i=0;i>a>>b;
add(a,b),add(b,a);
}
dfs(1);
cout< 树与图的广度优先遍历
图中点的层次
#include
#include
using namespace std;
const int N=1e5+10;
int h[N],e[N],ne[N],idx;
int d[N];
int q[N];
int n,m;
void add(int a,int b)//用于存储有向图
{
e[idx]=b,ne[idx]=h[a],h[a]=idx++;
}
int bfs()
{
int hh=0,tt=0;
q[0]=1;//存入1号节点
memset(d,-1,sizeof d);//用于判断是否遍历过
d[1]=0;//每个节点距离1号点的距离
while(hh<=tt)
{
int t=q[hh++];
for(int i=h[t];i!=-1;i=ne[i])//遍历t节点的每一个邻边
{
int j=e[i];
if(d[j]==-1)//没有遍历过
{
d[j]=d[t]+1;//加上到相邻节点的距离,每条边长为1
q[++tt]=j;
}
}
}
return d[n];
}
int main()
{
cin>>n>>m;
memset(h,-1,sizeof h);
for(int i=0;i>a>>b;
add(a,b);
}
cout<
拓扑排序
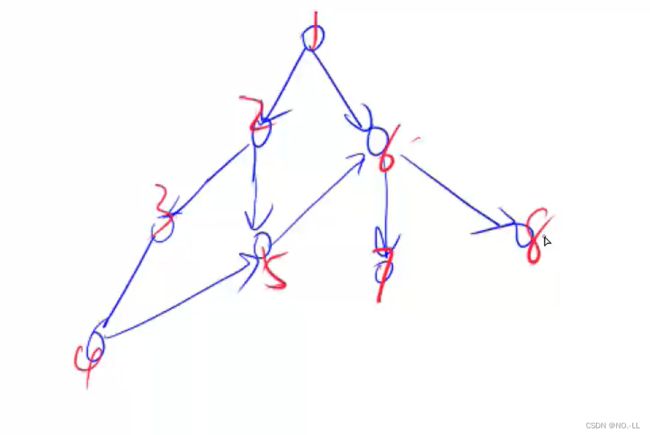
有向图的拓扑序列
一个有向图,如果图中有入度为 0 的点,就把这个点删掉,同时也删掉这个点所连的边。
一直进行上面出处理,如果所有点都能被删掉,则这个图可以进行拓扑排序。
思路:
- 用邻接表构造图,顺便记录各个节点的入度;
- 将如度为0的点入队
- 将队列里的点依次出队列,然后找出所有出队列这个点发出的边,删除边(邻接点入度减1),若该点入度减为0则入队,继续操作
- 若所有点入队则是拓扑排序
#include
#include
using namespace std;
const int N=100010;
int h[N],e[N],ne[N],idx;
int n,m;
int q[N],d[N];//q表示队列,d表示入度
void add(int a,int b)
{
e[idx]=b,ne[idx]=h[a],h[a]=idx++;
}
bool topsort()
{
int hh=0,tt=-1;
for(int i=1;i<=n;i++)
{
if(!d[i]) q[++tt]=i;//首先将入度为0的点入队
}
while(hh<=tt)
{
int t=q[hh++];//将t点出队
for(int i=h[t];i!=-1;i=ne[i])
{
int j=e[i];
d[j]--;//t点出队,t指向j的边删除,入度减1
if(d[j]==0) q[++tt]=j; //再将入度为0的点出队
}
}
return tt==n-1;//如果n个点都入队,则是拓扑图,返回true
}
int main()
{
cin>>n>>m;
memset(h,-1,sizeof h);
for(int i=0;i>a>>b;
add(a,b);
d[b]++;//a指向b,b的入度加1
}
if(topsort())
{
for(int i=0;i