mvp变换矩阵
下文所用到的图都是闫老师的games101中的图,games101的主页:https://sites.cs.ucsb.edu/~lingqi/teaching/games101.html
概述
mvp矩阵分别为模型(model),视图(view),投影(projection),是图形学中最基本的矩阵变化。模型要经过这三个变换才能在屏幕中正确的显示出来。
基础矩阵变换
基础的向量以及矩阵的计算不再多说,我们直接从矩阵的变换开始。
假设我们有一个点p(x,y),我们想让这个p点移到 ( 1 2 x . 1 2 y ) (\frac{1}{2}x.\frac{1}{2}y) (21x.21y)的位置。 x 1 = 1 2 x , y 1 = 1 2 y x_1=\frac{1}{2}x,y_1=\frac{1}{2}y x1=21x,y1=21y一个图形由无数个点组成,我们把它的点全都移到 1 2 的位置处 \frac{1}{2}的位置处 21的位置处,也就相当于把这个图形缩小了到了 1 2 \frac{1}{2} 21,把具体的参数抽象。用 s 1 s_1 s1代表x的方向的缩放, s 2 s_2 s2代表y方向的缩放: x 1 = s 1 ∗ x , y 1 = s 2 ∗ y x_1=s_1*x,y_1=s_2*y x1=s1∗x,y1=s2∗y写成矩阵的形式: [ x 1 y 1 ] = [ s 1 0 0 s 2 ] [ x y ] \begin{bmatrix} x_1 \\ y_1 \end{bmatrix}\quad=\begin{bmatrix} s_1 & 0 \\ 0 & s_2 \end{bmatrix}\quad \begin{bmatrix} x \\ y \end{bmatrix}\quad [x1y1]=[s100s2][xy] 类似的还有剪切(shear)变换,a和b是偏移量: x 1 = s 1 ∗ x + a ∗ y , y 1 = s 2 ∗ y + b ∗ x x_1=s_1*x+a*y,y_1=s_2*y+b*x x1=s1∗x+a∗y,y1=s2∗y+b∗x写成矩阵的形式 [ x 1 y 1 ] = [ s 1 a b s 2 ] [ x y ] \begin{bmatrix} x_1 \\ y_1 \end{bmatrix}\quad=\begin{bmatrix} s_1 & a \\ b & s_2 \end{bmatrix}\quad \begin{bmatrix} x \\ y \end{bmatrix}\quad [x1y1]=[s1bas2][xy]
接下来是旋转,在这里借用一下闫老师上课的图来说明一下:

要从左边的图旋转到右边的图,逆时针旋转θ度,假设左上角的点为(0,1)右下角为(1,0),旋转到的地方为图中所示,可以用公式表示
[ − s i n θ c o s θ ] = [ a b c d ] [ 0 1 ] \begin{bmatrix} -sinθ \\ cosθ \end{bmatrix}\quad=\begin{bmatrix} a & b \\ c & d \end{bmatrix}\quad \begin{bmatrix} 0 \\ 1 \end{bmatrix}\quad [−sinθcosθ]=[acbd][01] [ c o s θ s i n θ ] = [ a b c d ] [ 1 0 ] \begin{bmatrix} cosθ \\ sinθ \end{bmatrix}\quad=\begin{bmatrix} a & b \\ c & d \end{bmatrix}\quad \begin{bmatrix} 1 \\ 0 \end{bmatrix}\quad [cosθsinθ]=[acbd][10]可以分别算出abcd推导出旋转矩阵: [ c o s θ − s i n θ s i n θ c o s θ ] \begin{bmatrix} cosθ &-sinθ \\ sinθ &cosθ \end{bmatrix}\quad [cosθsinθ−sinθcosθ]旋转矩阵和缩放矩阵都是对自身进行操作,如果要将图形平移的话,需要引入额外的变量t来表示移动的距离: x = a x + t x=ax+t x=ax+t如果将3种变换一起使用的话: [ x 1 y 1 ] = [ a b c d ] [ x y ] + [ t x t y ] \begin{bmatrix} x_1 \\ y_1 \end{bmatrix}\quad=\begin{bmatrix} a & b \\ c & d \end{bmatrix}\quad \begin{bmatrix} x \\ y \end{bmatrix}\quad+\begin{bmatrix} t_x \\ t_y \end{bmatrix}\quad [x1y1]=[acbd][xy]+[txty]但这样就无法用一个矩阵表示所有的变换,所以我们要使用齐次坐标,将变换矩阵升维: [ x 1 y 1 w 1 ] = [ 1 0 t x 0 1 t y 0 0 1 ] [ x y 1 ] = [ x + t x y + t y 1 ] \begin{bmatrix} x_1 \\ y_1 \\w_1\end{bmatrix}\quad=\begin{bmatrix} 1 & 0 & t_x \\ 0 & 1 & t_y \\0 & 0 & 1\end{bmatrix}\quad \begin{bmatrix} x \\ y \\1\end{bmatrix}\quad=\begin{bmatrix} x+t_x \\ y+t_y \\1\end{bmatrix}\quad x1y1w1 = 100010txty1 xy1 = x+txy+ty1 这样对于一个二维的图形可以使用三维矩阵来进行变换,同时由于要用2维向量表示2维空间,我们规定: 2 D 的点表示为 ( x , y , 1 ) 2D的点表示为(x,y,1) 2D的点表示为(x,y,1) 2 D 的方向表示为 ( x , y , 0 ) 2D的方向表示为(x,y,0) 2D的方向表示为(x,y,0)这样点之间相减也可以得到方向。
整理之后得到统一的变换矩阵 [ x 1 y 1 1 ] = [ a b t x c d t y 0 0 1 ] [ x y 1 ] \begin{bmatrix} x_1 \\ y_1 \\1\end{bmatrix}\quad=\begin{bmatrix} a & b & t_x \\ c & d & t_y \\0 & 0 & 1\end{bmatrix}\quad \begin{bmatrix} x \\ y \\1\end{bmatrix}\quad x1y11 = ac0bd0txty1 xy1 矩阵的计算方式是右乘,也就是先从右边计算,注意区分先旋转还是先平移的区别。
对于3D的点(x/w,y/w,z/w)同样表示为4维(x,y,z,w)。3维变换如下: [ x 1 y 1 z 1 1 ] = [ a b c t x d e f t y h i j t z 0 0 0 1 ] [ x y z 1 ] \begin{bmatrix} x_1 \\ y_1 \\z_1\\1\end{bmatrix}\quad=\begin{bmatrix} a & b & c&t_x \\ d & e &f& t_y \\h&i&j& t_z\\0 & 0 &0& 1\end{bmatrix}\quad \begin{bmatrix} x \\ y \\z\\1\end{bmatrix}\quad x1y1z11 = adh0bei0cfj0txtytz1 xyz1
通常旋转等计算都是这样,但是这样就很难计算旋转的差值,所以引入了四元数的概念和罗德里格斯旋转公式,在这里就不展开了。
我们可以将这些基础的变换正式的应用到图形学中。
模型矩阵 Model
在3d游戏中,模型都是由美术们单独做好的,然后我们会将模型放到世界中,这一步变化叫做模型变换,完成这个变换的矩阵叫模型矩阵。模型矩阵转换为世界矩阵主要是为了统一坐标系,S代表缩放,R代表旋转,T代表平移
M m = S R T M_m=SRT Mm=SRT
视图矩阵 view
在世界坐标中还会根据摄像机的位置再次设置物体的位置,使摄像机呈现我们想要得到的画面,这一步叫做视图变换,完成这个变换的矩阵叫视图矩阵。
我们假设有一个摄像机,我们从摄像机的角度去观察物体,需要一个观察的起始点 o ( x 1 , y 1 , z 1 ) o(x_1,y_1,z_1) o(x1,y1,z1),一个指向物体的方向 g g g,一个向上的方向 t t t来确定方向。同时 g g g叉乘 t t t得到第三个方向 e e e

首先为了方便且规范,要摄像机移到原点的位置,然后向上的方向为 y y y轴,看向物体的方向为 − z -z −z方向, − z -z −z叉乘 y y y得到 x x x轴。为了保证看到的东西不变,将物体与摄像机做相同移动,我们把这个移动用矩阵表示出来.
首先要将摄像机从点 o ( x 1 , y 1 , z 1 ) o(x_1,y_1,z_1) o(x1,y1,z1) 移动到原点,移动矩阵为 T v = [ 1 0 0 − x 1 0 1 0 − y 1 0 0 1 − z 1 0 0 0 1 ] T_v=\begin{bmatrix} 1 & 0 & 0&-x_1 \\ 0 &1 &0& -y_1 \\0&0&1& -z_1\\0 & 0 &0& 1\end{bmatrix}\quad Tv= 100001000010−x1−y1−z11 然后进行旋转,将 g g g转到 − z -z −z,剩下两个轴做同样操作,但这样很难计算,所以我们反过来,将原点移到 o o o点然后再求出逆矩阵: R v − 1 = [ x g × t x t x − g 0 y g × t y t y − g 0 z g × t z t z − g 0 0 0 0 1 ] R^{-1}_v=\begin{bmatrix} x_{g×t} & x_t & x_{-g}&0 \\ y_{g×t} &y_t & y_{-g}&0 \\z_{g×t}&z_t & z_{-g}&0\\0 & 0 &0& 1\end{bmatrix}\quad Rv−1= xg×tyg×tzg×t0xtytzt0x−gy−gz−g00001 而R_v又是正交矩阵,正交矩阵的逆矩阵和转置矩阵是相等的,所以直接转置: R v = [ x g × t y g × t z g × t 0 x t y t z t 0 x − g y − g z − g 0 0 0 0 1 ] R_v=\begin{bmatrix} x_{g×t} & y_{g×t} & z_{g×t}&0 \\ x_t &y_t & z_t &0 \\x_{-g}&y_{-g} & z_{-g}&0\\0 & 0 &0& 1\end{bmatrix}\quad Rv= xg×txtx−g0yg×tyty−g0zg×tztz−g00001
先平移后旋转: M v = R v ∗ T v M_v=R_v*T_v Mv=Rv∗Tv
投影矩阵 Projection
投影变换是将3d物体投射到屏幕上变为我们能看到的2d物体,要让物体适应屏幕大小,简单的说就是把所有屏幕上能出现的物体压缩到-1到1,变成一个2x2大小的box(cvv,canonical view volume ,规则观察体)。首先还是先将物体的中心点,移动到原点,物体的x轴的中心是 左平面的 x 值 + 右平面的 x 值 2 \frac{左平面的x值+右平面的x值}{2} 2左平面的x值+右平面的x值其他两个轴同样原理,从这个点移到原点,所以是负的,写成矩阵如下:
[ 1 0 0 − 左平面的 x 值 + 右平面的 x 值 2 0 1 0 − 上平面的 x 值 + 下平面的 x 值 2 0 0 1 − 前平面的 x 值 + 后平面的 x 值 2 0 0 0 1 ] \begin{bmatrix} 1& 0 & 0&- \frac{左平面的x值+右平面的x值}{2}\\0 &1 & 0 &- \frac{上平面的x值+下平面的x值}{2}\\0&0 & 1&- \frac{前平面的x值+后平面的x值}{2}\\0 & 0 &0& 1\end{bmatrix}\quad 100001000010−2左平面的x值+右平面的x值−2上平面的x值+下平面的x值−2前平面的x值+后平面的x值1
注意这里的xyz的顺序,因为我们的摄像机是面朝 − z -z −z方向的,此时的坐标系是这样的:
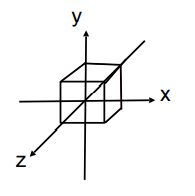
然后要进行原地的缩放,压缩到-1到1,所以还要乘以2得到矩阵: [ 2 r − l 0 0 0 0 2 t − b 0 0 0 0 2 n − f 0 0 0 0 1 ] \begin{bmatrix} \frac{2}{r-l}& 0 & 0&0\\0 & \frac{2}{t-b} & 0 &0\\0&0 & \frac{2}{n-f}&0\\0 & 0 &0& 1\end{bmatrix}\quad r−l20000t−b20000n−f200001 正交投影矩阵如下 M o r t h o = [ 2 r − l 0 0 0 0 2 t − b 0 0 0 0 2 n − f 0 0 0 0 1 ] [ 1 0 0 − 左平面的 x 值 + 右平面的 x 值 2 0 1 0 − 上平面的 x 值 + 下平面的 x 值 2 0 0 1 − 前平面的 x 值 + 后平面的 x 值 2 0 0 0 1 ] M_{ortho}=\begin{bmatrix} \frac{2}{r-l}& 0 & 0&0\\0 & \frac{2}{t-b} & 0 &0\\0&0 & \frac{2}{n-f}&0\\0 & 0 &0& 1\end{bmatrix}\quad \begin{bmatrix} 1& 0 & 0&- \frac{左平面的x值+右平面的x值}{2}\\0 &1 & 0 &- \frac{上平面的x值+下平面的x值}{2}\\0&0 & 1&- \frac{前平面的x值+后平面的x值}{2}\\0 & 0 &0& 1\end{bmatrix}\quad Mortho= r−l20000t−b20000n−f200001 100001000010−2左平面的x值+右平面的x值−2上平面的x值+下平面的x值−2前平面的x值+后平面的x值1
除了正交投影还有透视投影,透视投影是符合人眼视锥体的,可以产生近大远小,以及无限延伸的平行线会相交的现象。在这门课中没有直接推导,而是把正交投影给”挤“成了透视投影,是在正交投影的基础上进行的推导。
透视矩阵是将物体挤压到视锥体中
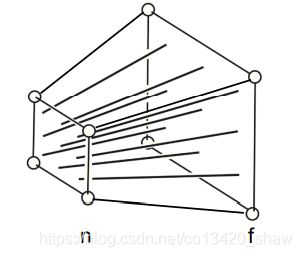
视锥体的边上是三角形的边,我们可以用相似三角形来求出边上的点的值。
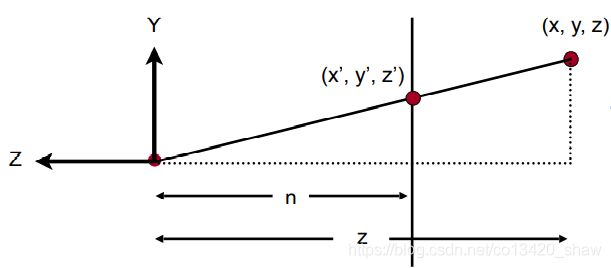
边上的某一点的值 y ′ = n z y y'=\frac{n}{z}y y′=zny,同理 x ′ = n z x x'=\frac{n}{z}x x′=znx,此时我们能知道的信息:
[ n z x n z y 未知 1 ] \begin{bmatrix} \frac{n}{z}x \\\frac{n}{z}y \\未知\\1\end{bmatrix}\quad znxzny未知1 可以乘上z: [ n x n y 未知 z ] \begin{bmatrix} nx \\ny \\未知\\z\end{bmatrix}\quad nxny未知z 假设从从正交投影变换成透视投影的矩阵为 M p e r s p − > o r t h o M_{persp->ortho} Mpersp−>ortho那么我们可以知道这个矩阵作用于这个矩阵可以得到: M p e r s p − > o r t h o [ x y z 1 ] = [ n x n y 未知 z ] M_{persp->ortho}\begin{bmatrix} x \\y \\z\\1\end{bmatrix}\quad=\begin{bmatrix} nx \\ny \\未知\\z\end{bmatrix}\quad Mpersp−>ortho xyz1 = nxny未知z 可以知道 M p e r s p − > o r t h o = [ n 0 0 0 0 n 0 0 ? ? ? ? 0 0 1 0 ] M_{persp->ortho}=\begin{bmatrix} n & 0 & 0&0 \\ 0 &n &0& 0 \\?&?&?& ?\\0 & 0 &1& 0\end{bmatrix}\quad Mpersp−>ortho= n0?00n?000?100?0 在做投影变换的时候有个特殊的地方,就是近平面上的点不变,对与近平面上的任意一点都有: [ x y z 1 ] = [ x y n 1 ] = [ n x n y n 2 n ] \begin{bmatrix} x \\y \\z\\1\end{bmatrix}\quad=\begin{bmatrix} x \\y \\n\\1\end{bmatrix}\quad=\begin{bmatrix} nx \\ny \\n^2\\n\end{bmatrix}\quad xyz1 = xyn1 = nxnyn2n 可以得出第三行的前两个数值为0。我们假设剩下的两个是为A,B,即 ( 0 , 0 , A , B ) (0,0,A,B) (0,0,A,B),此时在近平面上,第三行的值为 n 2 n^2 n2,可以得到: [ 0 0 A B ] [ x y n 1 ] = n 2 \begin{bmatrix} 0&0 &A&B\end{bmatrix}\quad\begin{bmatrix} x \\y \\n\\1\end{bmatrix}\quad=n^2 [00AB] xyn1 =n2 A n + B = n 2 An+B=n^2 An+B=n2,对于远平面上的中点 ( 0 , 0 , f , 1 ) (0,0,f,1) (0,0,f,1)同理,得到 A f + B = f 2 Af+B=f^2 Af+B=f2推出 M p e r s p − > o r t h o = [ n 0 0 0 0 n 0 0 0 0 n + f − n f 0 0 1 0 ] M_{persp->ortho}=\begin{bmatrix} n & 0 & 0&0 \\ 0 &n &0& 0 \\0&0&n+f& -nf\\0 & 0 &1& 0\end{bmatrix}\quad Mpersp−>ortho= n0000n0000n+f100−nf0 记得在使用的时候先转换成正交投影矩阵再应用这个矩阵。
最后来关注一下在正交矩阵挤压成投影矩阵的过程中,中间的点的z值。可以直接假设一个点代入进行计算,假设有一点 ( x , y , z , 1 ) (x,y,z,1) (x,y,z,1)在视锥体里: [ n 0 0 0 0 n 0 0 0 0 n + f − n f 0 0 1 0 ] [ x y z 1 ] = [ n x n y ( n + f ) z − n f z ] = [ x z y z n + f − n f z 1 ] \begin{bmatrix} n & 0 & 0&0 \\ 0 &n &0& 0 \\0&0&n+f& -nf\\0 & 0 &1& 0\end{bmatrix}\quad\begin{bmatrix} x\\ y \\z\\1\end{bmatrix}\quad=\begin{bmatrix} nx\\ ny \\(n+f)z-nf\\z\end{bmatrix}\quad=\begin{bmatrix} \frac{x}{z}\\\frac{y}{z} \\n+f-\frac{nf}{z}\\1\end{bmatrix}\quad n0000n0000n+f100−nf0 xyz1 = nxny(n+f)z−nfz = zxzyn+f−znf1 可以分别代入n,f的值分别演算一下。 f ( z ) = n + f − n f z 在 n < z < f 的范围内是大于 z 的,所以其中点的 z 值被推向远平面 f(z)=n+f-\frac{nf}{z}在n
通过fov求出需要的值
定义透视投影需要用到宽高比(Aspect ratio)和垂直的可视角度(fovY),有这两个值可以推导出其他我们需要的值、
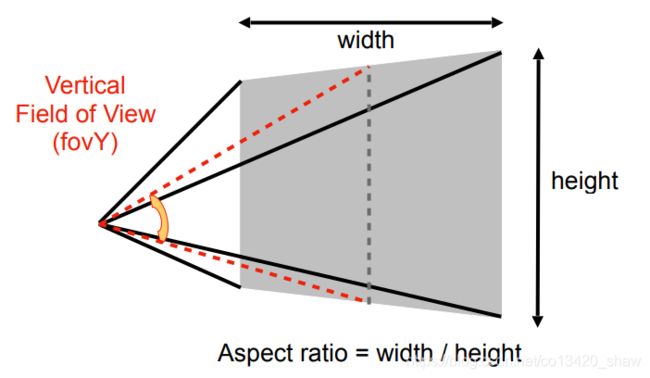

t a n f o v Y 2 = t ∣ n ∣ tan\frac{fovY}{2}=\frac{t}{|n|} tan2fovY=∣n∣t a s p e c t = r t aspect=\frac{r}{t} aspect=tr
可以通过这几个变量把几个面的值都求出来
关于NDC坐标
NDC坐标是归一化的设备坐标(Normalized Device Coordinates),实际上为了方便计算我们将点换到齐次坐标系,在进行透视投影之后,还要做透视除法,将xyzw都÷w,使最后一个值为1,回到笛卡尔坐标系。