算法与数据结构(一) 时间复杂度和循环不变量

1.什么是算法

Algorithm的本意：解决问题的方法.一系列解决问题的，清晰，可执行的计算机指令

2.循环不变量

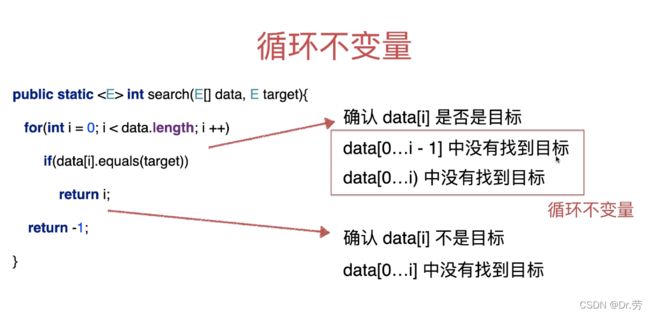
2.1线性查找法

   从数组中找到,找到我所需要的元素.

    public static  int search(E[] data, E target){

        for(int i = 0; i < data.length; i ++)
            if(data[i].equals(target))
                return i;

        return -1;
    }

2.2循环不变量

    以上面的线性查找法来看,满足循环不变量,才会进入到循环体中,而循环体,又是来维持循环不变量,即循环继续的条件.我每一轮循环开始都是满足data[0-i)这个区间没有找到目标,所以才开始循环,而循环体维持这个不变量,要么经过这轮循环就结束,要么继续下一轮循环,下一轮循环也满足data[0-i)这个区间没有找到目标.

   在算法初始,我们没有处理任何元素,说明我们在一个空区间中([0, -1]中),没有找到目标元素;处理完 i = 0 以后,如果没有找到目标元素,说明我们在包含一个元素的区间中（[0, 0] 中）,没有找到目标元素;处理完 i = 1 以后,如果没有找到目标元素，说明我们在包含两个元素的区间中（[0, 1] 中）,没有找到目标元素;

   循环不变量是为了帮助我们写出正确的代码.

 3.算法时间复杂度

   简单来说,时间复杂度这个概念,不是用来衡量一个算法的准确性能的,而是描述一个算法,随着 n 的逐渐增大,其算法性能的变化趋势.算法复杂度分析是“渐进分析”的一种（Asymptotic Analysis）,这里的“渐进”,就是这个意思.

   以上面的线性查找法为例,最差的情况下,我需要循环到整个数组最后一个元素即数组的长度n才能找到对应的元素,最好的情况下我想要找的元素是第一个.那么我们要用1还是n来表示时间复杂度呢?

   答案是:复杂度分析通常看最差的情况,表示算法运行的上界.用n表示算法的规模,也就是用例中的data.length.   T表示时间复杂度性能,只要知道与n是一个什么样正比的关系就可以,所以用例的时间复杂度使用T=O(n)表示.复杂度描述的是随着数据规模n的增加,算法性能的变化趋势,所以可以忽略常数.

   例如我T1=10000n,T2=2n^2,看上去n小的时候T1用的时间越长,但是别忘记了时间复杂度表示的是随着n的增大,算法性能的变化趋势,存在某一个n的时候,2n^2远远超过10000n.

4.常见的时间复杂度

•    logn

   如下,我需要求一个数字的二进制, 我们必须除以2,直到最后n为0.

   当数据增大n倍时,耗时增大logn倍(这里的log是以2为底的,比如,当数据增大256倍时,耗时只增大8倍

   底数不重要,以2为底和10为底就相册一个常数. 

•  √n

   求数字n的所有约数,即余数为0

   第一种方式,直接循环,判断余数是否为0,复杂度为n,但是我们知道10/2=5,2和5都是10的约数,所以我们改为第二种方式,他的复杂度为√n.

   时间复杂度不能仅仅看循环的次数.

• 2^n和n!

   1.长度为n的二进制数字,假设长度为3,3个二进制为可以表示的数字为0到7,即8个,现在我有n个位置,或者填0或者填1,为2^n.

   2.长度为n的数组的所有排列1*2*3...*n,即为n!.

•  常数

   无论我n有多大,常数次就可以得到结果

 总结:

   O(1) < O(logn) < O(√n) < O(nlogn) < O(n^2) < O(2^n) < O(n!)