深入浅出推荐系统(三):召回:协同过滤--永恒的经典
亚马逊作为商业化推荐系统的祖师,推出的开山之作便是协同过滤(collaborative filtering)。即使到了以深度学习为主流召回算法的今天,协同过滤仍然是推荐系统召回策略中绕不开的经典算法。它的思路简洁易懂,效果却出奇地好。今天,我们便来深入聊聊协同过滤算法。
什么是协同过滤
所谓“协同”,是指用户之间或物品之间的相似性,“过滤”则是指根据相似性,从大量物品中进行筛选的过程。这里说的相似性,并不等同于我们上一章中所讲的内容在语义上的相似。这里的“相似”,是与用户行为相关的,通常是指用户对物品的行为,主要是指评分,也包含点击、点赞、收藏、评论等隐性行为,当一群用户都对某几个物品进行操作,则这些物品便被认为是相似的。协同过滤认为,同样一群人喜欢的物品是相似的,反过来,喜欢同样物品的人,也是彼此相似的,它所蕴含的哲学思想便是“物以类聚,人以群分”。
协同过滤有两种形式:基于物品的协同过滤(Item-based CF)和基于用户的协同过滤(User-based CF)。在亚马逊上线协同过滤系统之后,顾客选择一本自己感兴趣的书,就会在底下看到一行"Customer Who Bought This Item Also Bought",这是基于Item的协同过滤;知乎、小红书等社交媒体上推荐信息流中你所关注的人“也关注了这个问题”或”点赞了这个帖子”便是基于User的协同过滤。
协同过滤算法原理
协同过滤的中心思路是计算物品之间的相似度,从而根据相似度进行排序,挑选出与用户操作过的物品最相似的若干物品(Item CF),或者计算用户之间的相似度,找到与目标用户相似的若干用户,将这些用户喜好的物品推荐给目标用户(User CF)。

计算相似度之前,需要构建用户与物品的评分矩阵。假设一个推荐网站有M个用户和N个物品,则评分矩阵如下:
I t e m U s e r ( r 11 r 12 ⋯ r 1 N r 21 r 22 ⋯ r 2 N ⋮ ⋮ ⋯ ⋮ r ( M − 1 ) 1 r ( M − 1 ) 2 ⋯ r ( M − 1 ) N r M 1 r M 2 ⋯ r M N ) \begin{array}{c}Item\end{array}\\ User \left( \begin{array}{cccc} r_{11} & r_{12} & \cdots & r_{1N} \\ r_{21} & r_{22} & \cdots & r_{2N} \\ \vdots & \vdots & \cdots & \vdots \\ r_{(M-1)1} & r_{(M-1)2} & \cdots & r_{(M-1)N} \\ r_{M1} & r_{M2} & \cdots & r_{MN} \\ \end{array} \right) ItemUser⎝⎜⎜⎜⎜⎜⎛r11r21⋮r(M−1)1rM1r12r22⋮r(M−1)2rM2⋯⋯⋯⋯⋯r1Nr2N⋮r(M−1)NrMN⎠⎟⎟⎟⎟⎟⎞
矩阵中每一行表示该行对应的用户对各个物品的评分,每一列表示该列对应的物品所获得的各个用户的评分。此处的评分依据具体的业务场景而定,通常情况下,对于电商、图书/电影评论类网站,分数为0-5分(半分为一档),或缺失值;而对于如信息流的点击行为来说,评分可以设置为0/1和缺失值。这样,物品的相似度便可以使用列向量之间的余弦距离来表示,如下:
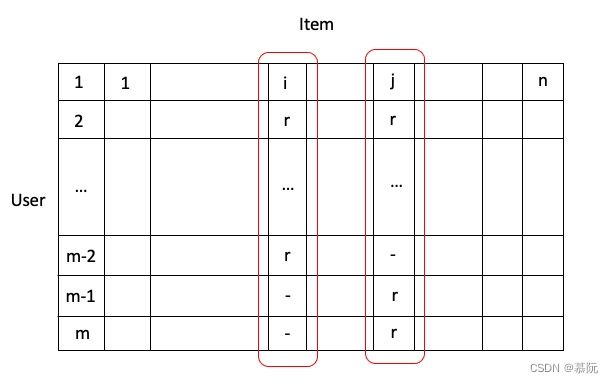
图中物品i和j的相似度表示如下:
s i m ( v i , v j ) = c o s ( v i ⃗ , v j ⃗ ) = v i ⃗ ∗ v j ⃗ ∣ ∣ v i ⃗ ∣ ∣ ∗ ∣ ∣ v j ⃗ ∣ ∣ sim(v_i, v_j) = cos(\vec{v_i}, \vec{v_j}) = \frac{\vec{v_i} * \vec{v_j}}{||\vec{v_i}|| * ||\vec{v_j}||} sim(vi,vj)=cos(vi,vj)=∣∣vi∣∣∗∣∣vj∣∣vi∗vj
有了用户对每个物品的打分(矩阵一般是稀疏的,大部分物品为0分),以及物品之间的相似度,便可以计算出用户对每个物品的潜在打分。从而可以按照评分降序排列,取头部物品推荐给用户。下面公式表示的是用户u对于未操作物品z的预测评分。其中 U s U_s Us表示用户评分过的物品。
s c o r e ( u , z ) = ∑ s i ∈ U s s c o r e ( u , s i ) ∗ s i m ( s i , z ) score(u, z) = \sum_{s_i \in U_s} { score(u, s_i) * sim(s_i, z)} score(u,z)=si∈Us∑score(u,si)∗sim(si,z)
通过以上公式,即可完成itemCF。对于userCF来说,用户相似度可以使用行向量之间的余弦距离来表示。
s i m ( u i , u j ) = c o s ( u i ⃗ , u j ⃗ ) = u i ⃗ ∗ u j ⃗ ∣ ∣ u i ⃗ ∣ ∣ ∗ ∣ ∣ u j ⃗ ∣ ∣ sim(u_i, u_j) = cos(\vec{u_i}, \vec{u_j}) = \frac{\vec{u_i} * \vec{u_j}}{||\vec{u_i}|| * ||\vec{u_j}||} sim(ui,uj)=cos(ui,uj)=∣∣ui∣∣∗∣∣uj∣∣ui∗uj
通过用户相似度和其他用户的评分,可以计算出用户对于其他物品的评分,由此可以基于评分进行降序排序,取topN推荐给用户了。
s c o r e ( u i , z ) = ∑ u j ∈ U s i m ( u i , u j ) ∗ s c o r e ( u j , z ) score(u_i, z) = \sum_{u_j \in U} { sim(u_i, u_j) * score(u_j, z) } score(ui,z)=uj∈U∑sim(ui,uj)∗score(uj,z)
协同过滤算法的思想至此介绍完毕。可以看出该算法思想易懂,公式简单,在各大公司的落地效果也很不错,可以兼顾点击转化等指标和惊喜度,因此得到了广泛的应用。
协同过滤数据处理
原理上来说,协同过滤很简单,但实现上却有一定难度。原因在于对于巨大的用户和物品的交叉矩阵来说,简单粗暴地计算每个用户对所有物品潜在打分,或者计算两两用户的相似度,是一个巨大的工程量,因此在实际的离线计算过程中,需要一定的数据处理技巧。
以Item CF为例,我们来看看该如何技巧性地计算物品相似度。看一下下面这个矩阵。
( ⋯ ⋯ ⋯ ⋯ ⋯ ⋯ r a i ⋯ r a j ⋯ ⋮ ⋮ ⋯ ⋮ ⋯ ⋯ r b i ⋯ r b j ⋯ ⋯ ⋯ ⋯ ⋯ ⋯ ) \left( \begin{array}{cccc} \cdots & \cdots & \cdots & \cdots & \cdots \\ \cdots & r_{ai} & \cdots & r_{aj} & \cdots \\ \vdots & \vdots & \cdots & \vdots & \cdots \\ \cdots & r_{bi} & \cdots & r_{bj} & \cdots \\ \cdots & \cdots & \cdots & \cdots & \cdots \\ \end{array} \right) ⎝⎜⎜⎜⎜⎜⎛⋯⋯⋮⋯⋯⋯rai⋮rbi⋯⋯⋯⋯⋯⋯⋯raj⋮rbj⋯⋯⋯⋯⋯⋯⎠⎟⎟⎟⎟⎟⎞
其中,r_{ai}和r_{aj}分别表示用户a对于物品i和j的打分。则计算i和j的相似度为如下公式:
s i m ( i , j ) = c o s ( i ⃗ , j ⃗ ) = . . . + r a i ∗ r a j + . . . + r b i ∗ r b j + . . . . . . + r a i ∗ r a i + . . . + r b i ∗ r b i + . . . + . . . + r a j ∗ r a j + . . . + r b j ∗ r b j + . . . sim(i, j) = cos(\vec{i}, \vec{j}) = \frac{... + r_{ai} * r_{aj} + ... + r_{bi} * r_{bj} + ...}{\sqrt{... + r_{ai} * r_{ai} + ... + r_{bi} * r_{bi} + ...} + \sqrt{... + r_{aj} * r_{aj} + ... + r_{bj} * r_{bj} + ...}} sim(i,j)=cos(i,j)=...+rai∗rai+...+rbi∗rbi+...+...+raj∗raj+...+rbj∗rbj+......+rai∗raj+...+rbi∗rbj+...
可以看出,当用户仅对i或仅对j进行打分时,分子乘积的展开项在用户a上为0,仅当用户既对物品i,又对物品j打分时,该项值才不为0,由此入手,以用户为key,计算每个用户对于不同物品两两之间的打分乘积,即上面乘积的每个展开项。
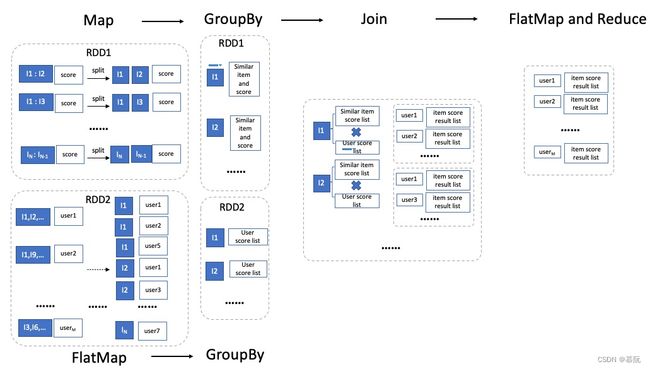
上图中的Map和GroupBy阶段展示了以用户粒度对Item打分进行聚合,再两两相乘的过程。
以MoiveLen数据集为例,record格式为:[userId, movieId, rating, timestamp],对该记录进行处理,上述逻辑的伪代码如下:
def get_single_multiply_result(record):
key = record[0]
lst = record[1]
result = []
sorted_lst = sorted(lst, key = lambda x : int(x[1]))
for i in range(0, len(sorted_lst)):
for j in range(i, len(sorted_lst)):
mul_score = float(sorted_lst[i][2]) * float(sorted_lst[j][2])
result.append(("%s_%s"%(sorted_lst[i][1], sorted_lst[j][1]), float(sorted_lst[i][2]), float(sorted_lst[j][2]), mul_score))
return result
#按照用户粒度,计算两两item打分的乘积
mul_rating_rdd = ratingFile.groupBy(lambda x : x[0]).flatMap(lambda x : get_single_multiply_result(x))
接着,以被同用户打分过两两item为key(虽然理论上两两item的笛卡尔积非常巨大,但实际上能够发生关联的item量级要远远小于理论值),对用户评分做聚合。这样,我们就得到了相似度计算公式中的分子,即将上面公式中分子各项乘积做加和。上图中的FlatMap和ReduceBy阶段展示了这一过程。该逻辑的相关代码如下:
def calculate_cos_dis(acc, cur):
numerator = 0.0
denominator_1 = 0.0
denominator_2 = 0.0
#分母加和
denominator_1 = acc[0] + cur[0] * cur[0]
denominator_2 = acc[1] + cur[1] * cur[1]
#分子加和
numerator = acc[2] + cur[2]
return (denominator_1, denominator_2, numerator)
cos_dis_rdd = mul_rating_rdd.reduceByKey(lambda acc, cur : calculate_cos_dis(acc, cur)).map(\
lambda x : (x[0], x[1][2] / (math.sqrt(x[1][0]) * math.sqrt(x[1][1]))))
至于分母的计算,同理,我们可以先按照用户分组,计算出单个用户下item评分的平方( r a j ∗ r a j r_{aj}*r_{aj} raj∗raj,实际上我们在以用户粒度进行聚合时,可以同时计算item评分笛卡尔积和item自身评分的平方,如上面代码所示),再以item为粒度,计算出该item评分向量的长度,即分母中的平方项。结合上面的分子,可以计算出两个向量最终的乘积。观察下上面的代码,事实上,我们可以在计算分子的时候同时计算了分母(将它们包入元组),以减少额外的rdd的产生。
有了物品两两间的相似度,就可以开始为用户推荐了。推荐的时候,既可以离线事先计算好,也可以在线推荐。
-
离线计算仍然需要一定的数据处理技巧:
-
在线推荐则可以将每个item的相似头部item存储入线上可访问存储(如Redis);同时通过实时流订阅用户行为,将用户近日行为存入线上可访问的存储中,对用户进行推荐时,则实时取出用户操作过的item及根据操作时间计算的评分,同时取出用户操作物品和这些物品的相似物品,直接进行线上评分预测并做排序截断。
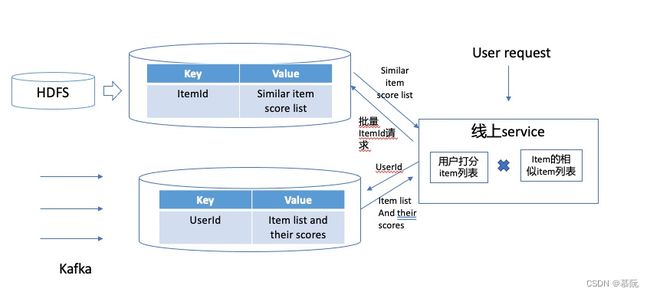
在线推荐的好处是可以捕获用户的实时兴趣,即时性更好。但对线上工程有一定的性能要求。
矩阵分解法破解协同过滤
除了通过数据处理技巧来实施协同过滤算法,这套算法本身也有一些被广泛使用的求解方式。最为常见的便是矩阵分解。其思想如下:
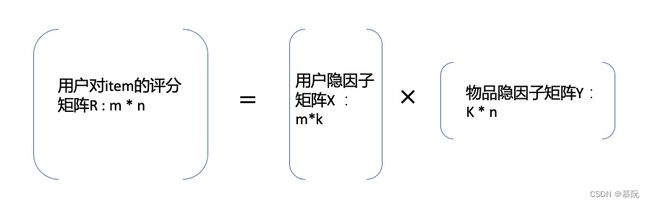
实际上是将用户打分矩阵转化为两个较小的矩阵相乘,其中k为超参数,k维向量空间的每个维度代表一个隐因子(latent factor),“隐”字传递的意思是,向量并不具备可解释性,可近似理解为item的语义,k越大,语义越丰富。
矩阵相乘的思想是将稀疏的用户评分矩阵转化成两个稠密的用户矩阵和物品矩阵,从而通过矩阵相乘,填补用户没有评分的缺失项,完成用户对其他物品的评分预测。由此,我们的工作就变成了求解两个稠密矩阵,那该如何求解呢?在矩阵相乘后,用户u对物品i的评分可以看作如下两个向量相乘:
r u i ′ = ( x u 1 x u 2 ⋯ x u ( k − 1 ) x u k ) × ( y 1 i y 2 i ⋮ y ( k − 1 ) i y k i ) r_{ui}' = \begin{array}{lc} \left( \begin{array}{c} x_{u1} & x_{u2} & \cdots & x_{u(k-1)} & x_{uk} \\ \end{array} \right) \end{array} \times \begin{array}{lc} \left( \begin{array}{c} y_{1i} \\ y_{2i} \\ \vdots \\ y_{(k-1)i} \\ y_{ki} \\ \end{array} \right) \end{array} rui′=(xu1xu2⋯xu(k−1)xuk)×⎝⎜⎜⎜⎜⎜⎛y1iy2i⋮y(k−1)iyki⎠⎟⎟⎟⎟⎟⎞
用户u在物品i上的真实评分为 r u i r_{ui} rui,则两者的平方误差为:
( r u i − r u i ′ ) 2 = ( r u i − x u T y i ) 2 (r_{ui} - r_{ui}')^2 = (r_{ui} - x_u^Ty_i)^2 (rui−rui′)2=(rui−xuTyi)2
因此,我们需要做的便是最小化平方误差损失函数: m i n ∑ ( r u i − x u T y i ) 2 min\sum(r_{ui} - x_u^Ty_i)^2 min∑(rui−xuTyi)2,为防止过拟合,一般会加入L2正则项,即: m i n ∑ ( r u i − x u T y i ) 2 + λ ( ∣ x u ∣ 2 + ∣ y i ∣ 2 ) min\sum(r_{ui} - x_u^Ty_i)^2 + \lambda(|x_u|^2 + |y_i|^2) min∑(rui−xuTyi)2+λ(∣xu∣2+∣yi∣2)。
工程上,一般有两种求解方法,SGD(Stochastic Gradient Descent随机梯度下降)和ALS(Alternating Least Squares,交替最小二乘法)。前者通过优化真实评分和预测评分的误差来进行,但在海量数据的背景下,一般较难使用单机进行SGD求解。
ALS其名字即为算法本身,即通过交替优化用户隐因子矩阵 X X X和商品隐因子矩阵 Y Y Y来求的最优解。一般过程是先固定 Y Y Y,使得公式变成关于 X X X的二次函数,使用最小二乘法求解,求出最优 X X X。接着固定 X X X,再对 Y Y Y使用最小二乘法求解,如此交替,直到收敛。Spark mllib中提供了ALS算法的封装,可以直接使用。
from pyspark.ml.recommendation import ALS
#设定最大迭代次数、正则项参数、column名字等
als = ALS(maxIter=5, regParam=0.01, userCol="userId", itemCol="movieId", ratingCol="rating")
model = als.fit(training)
协同过滤的适用场景
从场景来说,item CF适合user较多,item更新相对不频繁的场景,如电商、视频、电影点评类网站,而user CF则适用于item经常大量更新,而user相对稳定的场景,如新闻、社交媒体、博客等。
从精确度上来说,item CF由于是基于用户历史偏好来推荐,因此可解释性更好,在电商中直接加入“这本书跟你之前买过的xx很相似”,是一个说服用户进行点击的好理由。而“与你有相同喜好的用户也喜欢这本xx”,或者“猜你喜欢”,作为推荐理由则更弱一些。然而在社交类或新闻类网站,user CF的推荐由于更具有多样性,能够提供给用户更多的惊喜度。尤其是新闻类网站,往往会倾向推荐出热门内容,所以更容易吸引用户的兴趣。
从覆盖角度看,对单个用户来说,user CF能够提供更好的多样性,因为它能覆盖更多物品(因为所推荐物品相较于item CF,与用户历史偏好的相关性会更弱);但对于整个系统而言,item CF由于擅长覆盖长尾物品(因为只要有一些用户对两个物品同时操作,则两个物品就会有较高相似度),因此在系统层面上看,item CF会覆盖更多物品,而user CF则会偏向推荐热门物品(因为user CF可推荐物品较多,只有大量用户对某个物品发生过操作,才有可能在权重排序过程中被推荐出来,最终导致推荐给大部分用户的,都是较为相似的热门物品),因此在系统整体覆盖上,user CF会相对较低。
实际使用中,一般推荐系统会同时存在两种推荐算法,用于不同场景的推荐。(如“猜你喜欢”会使用user CF,而“看了又看”会使用item CF,等)。
优势与劣势
协同过滤仅基于用户对物品的操作记录进行计算,不像内容推荐那样依赖于自然语言处理技术,所以实现简单。从效果上来说,如前面所述,协同过滤算法相对于基于内容的推荐,多样性会更好,会给用户带来更多的惊喜,且推荐精准度更高,实践的指标表现会更好。
但协同过滤也存在着一定的不足,对于冷启动的情况,仍然无法解决。新加入的物品,由于缺乏足够的用户操作记录,很难在协同过滤中被推荐出来;此外,新加入的用户,由于没有历史记录,就很难通过Item CF来推荐相似物品,或通过User CF找到相似用户来做物品推荐。所以,协同过滤尽管有着实现简单且效果不错的优点,仍然不能作为单一的召回渠道,而需要其他召回渠道配合,以进一步提升召回物品的丰富性。
扩展:协同过滤与频繁集挖掘的关联
接触过数据挖掘的朋友应该知道频繁集挖掘算法,其最经典的案例便是“啤酒和尿布”。乍一听频繁集挖掘和协同过滤似乎是毫不相关的两个东西,但仔细想下,就会发现Item CF和频繁集挖掘的本质都是寻找关联度较高的物品,那两者有什么不同之处呢?
从场景上看,两者采用的数据有一定的区别,频繁集挖掘也叫“购物篮分析”,分析的是同一次购买行为下的共现物品,因此,频繁集挖掘实际是以行为为粒度来构建物品间的关系;而协同过滤则是以用户为粒度来构建物品关联,举个例子,用户昨天买了手机,今天买了充电器,则在频繁集挖掘中两者不会被关联,而在协同过滤中则会被关联。(当然,此处我们窄化了频繁集挖掘的场景,宽泛地讲,频繁集挖掘当然也可以跨单次购物来分析,但一般来说,都是以行为为粒度来计算)。
此外,协同过滤使用了用户评分用于权重计算,而频繁集挖掘则更关注共现次数,对于打分则不大关注。因此,协同过滤应该比频繁集挖掘能够产生更精准的推荐。
从算法实现上,两者也有一定差别。频繁集挖掘需要设定支持度阈值,只有超过阈值的两个物品才认为是频繁共现的,协同过滤要求则较为宽松。
总之,协同过滤是推荐系统所采用的名字,它的理论基础是频繁集挖掘,但是针对具体目标做了更多的调整,使之更适用于推荐系统。