北航计算机组成原理课程设计-2021秋 PreProject-MIPS-MIPS 汇编程序设计

北航计算机学院-计算机组成原理课程设计-2021秋

PreProject-MIPS

MIPS 汇编程序设计

---

本系列所有博客，知识讲解、习题以及答案均由北航计算机学院计算机组成原理课程组创作，解析部分由笔者创作，如有侵权联系删除。

---

从本节开始，课程组给出的教程中增添了很多视频讲解。为了避免侵权，本系列博客将不会搬运课程组的视频讲解，而对于文字讲解也会相应地加以调整，重点在于根据笔者自己的理解给出习题的解析。因此带来的讲解不到位敬请见谅。

---

条件语句

汇编语言本身是十分灵活的，但是这种灵活性可能会造成理解和编写上的困难，而模式化可以降低理解上的难度也可以让大家编写汇编语言代码时更加得心应手。这里将以程序中两种极其普遍的语句——条件语句与循环语句为例，做简单分析。首先来看条件语句：

.text
li $t1, 100             #t1 = 100
li $t2, 200             #t2 = 200
slt $t3, $t1, $t2       #if(t1 < t2) t3 = 1 
beq $t3, $0, if_1_else
nop
#do something
j if_1_end              #jump to end
nop
if_1_else:
#do something else

if_1_end:
li $v0, 10
syscall

这里展示了一个最简单的 if/else 语句，这段代码实现的功能非常简单，就是判断 $t1 和 $t2 两个寄存器中所储存的值的大小。如果 $t1 < $t2 则 do something 否则 do something else。

这段代码的核心实际上在第 5 行，第 5 行判断是否跳转决定了到底是执行 do something 还是执行 do something else。如果判断条件 $t1 < $t2 为真，即 t3 == 1，则不会跳转，继续执行 do something ，否则 t3==0，会跳转到 if_1_else 继续执行 do something else, 从而实现了 if($t1 < $t2) {do something} else {do something else} 的功能

同学们可以进一步思考 if/else if/else 语句以及switch语句该如何编写？如果条件变得更加复杂又该如何编写？

循环语句

.text
li $t1, 100             #n = 100
li $t2, 0               #i

for_begin1:             #for (int i = 0; i < n; i++)
slt $t3, $t2, $t1       #{
beq $t3, $0, for_end1  
nop        
#do something
addi $t2, $t2, 1        #i++
j for_begin1
nop                     #}    

for_end1:
li $v0, 10
syscall

上面的代码给出了一个标准 C 语言中 for 循环语句的汇编语言写法。

• 2，3 行初始化了 n 和 i.
• 6 行判断 i < n 是否为真，如果为真则第 7 行的 beq 不会跳转，否则跳转到 15 行结束程序。
• 9 行可以替换为需要在循环体内执行的代码。
• 10 行自增循环变量。
• 11 行跳回 5 行进行判断。

同学们请在此基础上进行扩充，并结合上一小节条件语句的写法，尝试一下如何编写多重循环语句，以及 while 循环和 do while 循环，并比较这几个循环之间的区别。

接下来我们将开始学习编写较为复杂的汇编程序。

需求分析

为了帮助大家更快的掌握汇编语言编程，在这里我们将带着大家一起设计一个简单的排序程序：对输入的 n 个整数进行排序后输出。相信在大一学习 C 语言时，同学们都已经学习过了相关的算法和 C 语言程序编写方法。那么使用汇编语言后，程序的行数势必会变长，但其原理是完全相同的。

事实上，为了实现功能，我们有两种实现思路：

• 只要求最终程序结果相同
• 在程序运行结果相同的情况下，使用汇编语言满足 C 语言程序的结构，模仿 C 语言程序的控制流、数据结构等。

简单想一想，前一种实现方法的行数势必会比后一种实现方法的代码量要少。但长远来看，由于汇编语言具有高度的灵活性而结构性、抽象性较差，当我们试图修改或扩展程序功能时，其结果就是难以修改，并且也难以查错。同时，也为了能更加详细地讲解汇编语言程序设计，我们将采用第二种实现思路来进行编写。

**注意：**在本讲的代码中，考虑了延迟槽，也就是说执行每条跳转指令后（无论是否跳转）都会执行它的下一条指令。延时槽的知识在此并不重要，只是让大家先认识一下，在后面的学习中会作为重点内容出现。而在本部分的代码中，将不会真正用到延时槽（即所有延时槽中都为 nop 指令）。

接下来我们可以把对上述排序题的分析总结为编程思路：

1. 要有输入输出提示语句
2. 先输入整数的个数 n，再输入 n 个整数。
3. 能够读取 n 个整数输入，并保存在内存中。
4. 要对 n 个整数进行从小到大排序，这里采用选择排序法。
5. 将排序后的整数进行输出。

程序结构设计

[视频]

为了方便理解，我们仿照C语言来对程序进行分解。按照功能模块来分，程序可以分为 6 个部分：数据定义、主函数、输入部分、输出部分、排序部分、寻找最小值部分。

注意，虽然这里使用了“函数”一词，但这只是为了便于理解，事实上并不需要写成一个完整的“函数”，只需能将不同的功能区分开，便于理解即可。

1. 首先，程序需要声明几个内存区域来存储数列、字符串、临时变量等。
2. 然后来到主函数，主函数依次调用输入函数、排序函数和输出函数。
3. 排序函数循环调用寻找最小值部分，传递给寻找最小值部分想要遍历的范围，而寻找最小值部分则返回一个最小值的地址，以供排序部分进行交换。
4. 最终，程序结束，完成功能。

关于通用寄存器的使用，实际上是一种约定，为了方便程序员之间的沟通而制定的规则。

1. 对于 s 寄存器而言，被调用者需要保证寄存器中的值在调用前后不能发生改变——对应到实际操作中，如果你想要编写一个子函数，那么在这个子函数中使用的所有 s 寄存器，都必须要在函数的开头入栈，在函数的结尾出栈，以确保其值在这个函数被调用前后不会发生变化。
2. 对于 t 寄存器而言则刚好相反，你编写的子函数中用到 t 寄存器的地方无需做任何保存，随意使用即可——因为维护 t 寄存器是上层函数的任务。这也就是所谓的 “s 寄存器由被调用者维护，t 寄存器由调用者维护”。
3. 需要注意的是，这仅仅是一个约定而已。你当然可以不遵守这种规范，但代价就是程序的合作和维护将变得举步维艰。在同学们编写 mips 代码的时候，尤其是涉及到子函数的编写时，我们推荐严格按照 mips 的规范进行，确保一个函数在被调用前后，其中所用到的 s 寄存器的值不会被改变。

一个调用者（即父函数）并不能预知其将要调用的子函数（即被调用者）会使用到哪些 t 寄存器，但可能在调用时并不想失去自己正在使用的某个 t 寄存器中的数据。

在这种情况下，为了维持 t 寄存器中的数据，调用者有两种选择：一是将所有 t 寄存器中的数据移至 s 寄存器，函数调用结束之后再移回来；二是将自己希望保留的 t 寄存器压入栈中，函数调用结束之后再弹回来。

第一种方法看似简单，但实际上引入了很多潜在的问题，比如：s 寄存器用完了怎么办？怎么确保子函数一定不会破坏 s 寄存器中的数据？在自动生成汇编代码（如编译）的过程中，怎样确定哪些 s 寄存器是可以用来保存 t 寄存器中的数据的？

因此，采用第二种方法，是一个更优雅，也更规范的做法。在第二种方法里，不再需要去考虑寄存器之间如何倒腾，只需要借助 sp 指针，不停地用栈去存取自己需要的数据就可以了。这减少了程序员的心智负担，规范了函数调用的过程，也方便了编译器的实现。

总而言之，调用者维护 t 寄存器，被调用者维护 s 寄存器的意义，就在于让代码更易于模块化。在这种约定下，调用者不需要去考虑被调用者的具体细节，被调用者也不需要去考虑自己被调用的方式。这使得 mips 代码可以以函数为单位进行模块化开发。

数据声明与分配

[视频]

控制流

[视频]

输入与输出

[视频]

排序与子过程调用

[视频]

练习：闰年

闰年

实现满足下面功能的汇编程序：

输入一个年份 ,判断 是否为闰年。

输入格式

输入一个整数 。

输出格式

输出 0 或者 1。输出 0 代表 不是闰年，输出 1 代表 是闰年。

约定

1、

2、请勿使用 .globl main

3、请使用 syscall 结束程序：

li $v0, 10
syscall

输入样例

1900

输出样例

0

输入样例

2004  

输出样例

1

提交要求

• 请勿使用 .globl main。
• 不考虑延迟槽。
• 只需要提交 .asm 文件。
• 程序的初始地址设置（Mars->Settings->Memory Configuration）为 Compact,Data at Address 0。

练习：矩阵转化

矩阵转化

实现满足下面功能的汇编程序：

输入一个 乘 的稀疏矩阵 （矩阵每个元素为占一个字的整数），将 转化为三元组列表(该列表的排列顺序为：行号小的在前，如果行号相同则列号小的在前)，并将三元组列表逆序输出。

输入格式

第一行是一个整数 ,第二行是一个整数 。接下来的 乘 行每行一个整数，矩阵 的第 行，第 列的元素，为上述输入的第 个整数（即一行一行地输入矩阵 的每一个元素）。

输出格式

x 行，按照输入顺序的逆序输出 x 个非 0 元素的信息：每行输出 3 个整数，依次为矩阵非 0 元素对应的行数，列数和数值，中间以空格隔开。

约定

1、

2、

3、矩阵每个元素值占一个整数

4、请勿使用.globl main

5、请使用syscall结束程序：

li $v0,10
syscall

输入样例

2
4
1
0
0
0
5
0
0
0

输出样例

2 1 5
1 1 1  

提交要求

• 请勿使用 .globl main。
• 不考虑延迟槽。
• 只需要提交 .asm文件。
• 程序的初始地址设置（Mars->Settings->Memory Configuration）为 Compact,Data at Address 0。

递归程序解析

简介

在 C 语言中我们学过递归的思想，即在函数的定义中调用自身的方法。通过调用自身的方式，我们可以实现复杂的函数功能。我们先来看一个简单的，在 C 语言中使用递归计算阶乘的例子。

C 语言阶乘

如果我们要实现一个求阶乘的函数，我们在 C 语言中可以这么写：

factorial 函数里面第一句是递归终止条件，一般来说，我们在递归程序中都要设置递归终止条件，否则函数会一直递归下去直到触发异常。第二句是调用自身的体现，我们通过这句话完成函数的递归实现。

MIPS 汇编阶乘

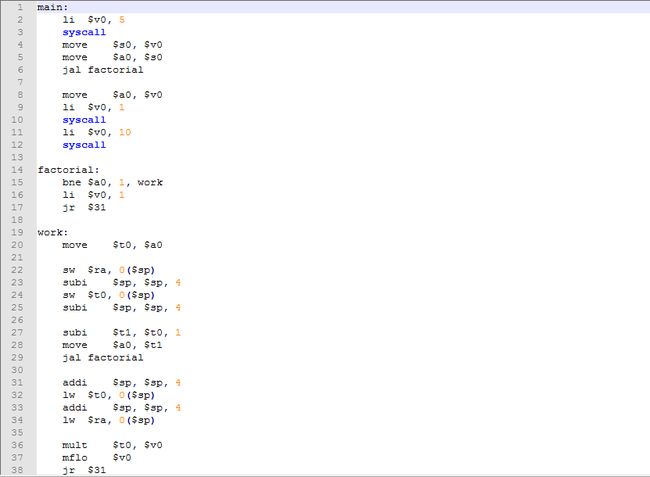
使用汇编语言的话，我们可以写成如下样式：

写成汇编形式以后立马长了很多，但是不用怕，我们一点点来分析这个程序。

首先是主程序部分，前三句将我们需要计算的 nn 存入到寄存器 $s0 中。之后我们再将这个变量的值放回 $a0 里面。为什么要把 nn 的值存到 $a0 这个寄存器中呢。因为从习惯上，我们一般把需要传递的变量放到 $a0, $a1 中。之后我们在第五句的时候，通过 jal 指令跳转到 factorial 函数。为什么这里我们选择 jal 而非 j 呢？我们知道j指令可以直接跳转到 label 的位置，jal 与其相比多了一个将 \tt{PC+4}PC+4 写入 31 号寄存器的过程。这样做的最大的好处在于，当我们函数结束时，我们可以通过jr 函数跳转回之前的位置。就像我们在 C 语言中，函数运行完后，会返回到之前调用它的位置，并执行下一条指令。所以在函数调用时，我们往往会搭配使用 jal 和 jr。

下来就是重头戏了。我们来分析下 factorial 部分。最开始的三句，其作用等价于我们在 C 语言 factorial 函数中的第一句，即递归终止条件。如果此时 $a0 的值为 1，那么会将值 1 写在 $v0 寄存器里。意味着 1 的阶乘值为 1。如果 $a0 的值不为 1，我们跳转到 work 部分。这部分主要实现的是递归调用。第一句，我们将 $t0 的值设置为 $a0，即当前 nn 的值。接下来我们要将当前这个函数中用到的值存入栈中。有用的值有两个，一个是当前 nn 的值，因为我们要利用它进行计算。另一个是当前的 $ra 寄存器的值，因为此时的 $ra 的值可能在后面被 jal 指令再次覆盖，以至于无法跳转到正确的位置。这里需要注意下栈的增长方向，应该是从高到低。所以我们存入一个数之后要将当前 $sp 的值减去 4，一遍下一个数的存放。接着我们要设置传递给下一次函数的参数。具体来说就是 n-1n−1 的值。我们将其存入 $a0 中。做好所有这些准备工作，我们就可以进行递归了，通过 jal 指令再次调用 factorial 函数。在调用结束后，因为我们巧妙的设计，下一层函数结束后将通过 jr 指令跳转这里，并接着执行下一条的内容。之前我们将 $t0 和 $ra 的值存入到了栈中，相应的，我们这里需要将这些值重新写入。并且恢复栈指针的位置。之后我们计算 nn 与下一层函数返回值的乘积，并且当做新的返回值存入 $v0 之中。最后我们通过 jr 指令，返回到上一次调用它的地方。

我们对比下 C 语言的实现和 MIPS 汇编的实现。其实两者的差距主要在于两个部分。第一，C 语言中，函数内的临时变量是不需要程序员来通过栈维护的。我们可以理解为，每一层的变量相互之间都是独立的。但是在 mips 汇编中，我们需要维护这些变量。第二，我们需要维护 PC 值的变化。C 语言中函数结束会自动返回到调用它的位置。但是在 mips 汇编中，我们需要利用 jal 和 jr 来实现这个功能。

challenge！哈密顿回路

哈密顿回路

实现满足下面功能的汇编程序：

输入一个具有 个顶点的无向图 ，判断 是否有哈密尔顿回路。（哈密顿回路问题，建议使用递归解决）

输入格式

第一行是一个整数 ，代表 有 个顶点，第二行是一个整数 ，代表 有 条边，接下来的 行，每行具有一个整数，设每个奇数行的数为 ,它下一行的数 ，序号为 , 的两个顶点间具有一条边，两个整数之间以回车隔开（点的标号从 1 开始）

输出格式

输出一个整数，若为 0 则代表 不具有哈密尔顿回路，若为 1 则代表 具有哈密尔顿回路。

约定

1、

2、

3、请勿使用 .globl main

4、最大运行指令条数限制为 100000

5、请使用 syscall 结束程序：

li $v0, 10
syscall

输入样例

5
6
1
2
1
3
2
3
2
4
3
5
4
5

输出样例

1

输入样例

5
6
1
2
1
3
2
3
2
4
1
4
4
5  

输出样例

0  

提交要求

• 请勿使用 .globl main。
• 不考虑延迟槽。
• 只需要提交 .asm 文件。
• 程序的初始地址设置（Mars->Settings->Memory Configuration）为Compact,Data at Address 0。