佳木斯集训Day2例题 数论
由于今天良心学长的题解非常详细还附带标程 以及我答的特别水 所以今天做例题的博客…
今天的专题是数论----欧拉函数、欧拉定理、费马小定理、中国剩余定理
一想起要打公式就头皮发麻…所以我有可能粘图片
Gcd(bzoj2818)
fzoj4284
题目描述
给定整数N,求1<=x,y<=N且Gcd(x,y)为素数的数对(x,y)有多少对.
输入
一个整数N
输出
如题
样例输入
4
样例输出
4
显然我们需要枚举 g c d ( x , y ) gcd(x,y) gcd(x,y),对于每个素数 p = g c d ( x , y ) p=gcd(x,y) p=gcd(x,y) 对答案的贡献为 1 1 1到 ⌊ n p ⌋ \left \lfloor \frac{n} {p} \right \rfloor ⌊pn⌋的有序互质对 ( x , y ) (x,y) (x,y)的个数
当 y = x y=x y=x时 有且仅有 y = x = 1 y=x=1 y=x=1
当 y > x y>x y>x时 有序互质对 ( x , y ) (x,y) (x,y)的个数为小于y与y互质的数的个数,即y的欧拉函数 Φ ( y ) \Phi(y) Φ(y)
同理,当x>y时 有序互质对 ( x , y ) (x,y) (x,y)为 Φ ( x ) \Phi(x) Φ(x)
所以 a n s = ∑ p ∈ P 2 ∑ i = 1 ⌊ n p ⌋ C Φ ( i ) − 1 ans=\sum_{p\in P} 2\sum_{i=1}^{\left \lfloor \frac{n} {p} \right \rfloor}C\Phi(i) -1 ans=∑p∈P2∑i=1⌊pn⌋CΦ(i)−1
只需线性筛欧拉函数 再求出前缀和就ojbkk了
#include欧拉心算(bzoj4804)
fzoj5383
这道题要用到数论分块
首先什么是数论分块 顾名思义就是分块在数论上的应用
不过非常神奇的一点是你如果不会分块但你还是可以会数论分块的
先看一道题理解一下数论分块
题目描述
给出正整数n和k,计算j(n, k)=k mod 1 + k mod 2 + k mod 3 + … + k mod n的值,其中k mod i表示k除以i的余数。例如j(5, 3)=3 mod 1 + 3 mod 2 + 3 mod 3 + 3 mod 4 + 3 mod 5=0+1+0+3+3=7
输入
输入仅一行,包含两个整数n, k。
输出
输出仅一行,即j(n, k)
样例输入
5 3
样例输出
7
所求为
∑ i = 1 n k m o d i \sum_{i=1}^{n}k mod i i=1∑nkmodi
为了应用数论分块 将这个式子改为:
∑ i = 1 n k − i × ( ⌊ k i ⌋ ) \sum_{i=1}^{n}k-i×(\left \lfloor \frac{k} {i} \right \rfloor) i=1∑nk−i×(⌊ik⌋)
前面的 n × k n×k n×k直接先算出来
后面的 i i i是单增的
而 ⌊ k i ⌋ \left \lfloor \frac{k} {i} \right \rfloor ⌊ik⌋在一段范围内是相等的 总共只有 2 n 种 取 值 2\sqrt{n}种取值 2n种取值
因此,每次求出这一段范围,直接计算等差数列即可
代码如下:
#include好了偏题了 大家应该对数论分块有理解了 那么我们回到正题
题目描述
给出一个数字N,求
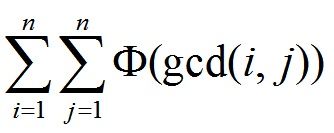
输入
第一行为一个正整数T,表示数据组数。
接下来T行为询问,每行包含一个正整数N。
T<=5000,N<=10^7
输出
如题
样例输入
4
样例输出
4
一步一步的化简到这里
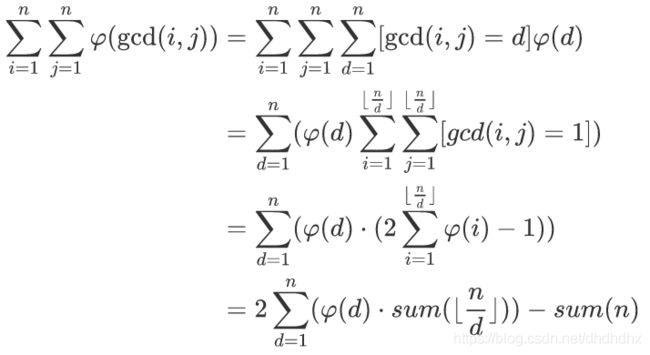
最后一行减号左边用数论分块
代码如下:
#include今天先发两个吧 后面的我会补上去的
有问题可以发在评论区或者加 Q Q 407694747 QQ407694747 QQ407694747一起讨论
各位大佬各路神犇请多多指教