【题解】2023牛客寒假算法基础集训营2

A. Tokitsukaze and a+b=n (easy)

思路

tag: 枚举 暴力
数据范围很小，可以直接暴力。

int n;
void solve()
{
    cin>>n;
    int l1,r1,l2,r2;
    cin>>l1>>r1>>l2>>r2;
    int res=0;
    set<PII>s;
    rep(i,l1,r1)
        if(n-i>=l2&&n-i<=r2)s.insert({i,n-i});
    cout<<s.size()<<endl;
}

B. Tokitsukaze and a+b=n (medium)

思路

tag: 贪心，二分
这题相对于A在范围上进行了扩大，所以不能采用暴力做法，不难发现，当第一个区间选取的越靠右时，则在第二个区间选取就越靠左，反之也成立，此时题目就对应了二分的两种板子做法（当然此题也可以O(1)写，这里不在赘述。

int n;
void solve()
{
    cin>>n;
    map<int,int>mp;
    int l1,r1,l2,r2;
    cin>>l1>>r1>>l2>>r2;
    int l=l1-1,r=r1;
    while(l<r)
    {
        int mid=l+r+1>>1;
        if(n-mid>=l2)l=mid;
        else r=mid-1;
    }
    int x=l;
    l=l1,r=r1+1;
    while(l<r)
    {
        int mid=l+r>>1;
        if(n-mid<=r2)r=mid;
        else l=mid+1;
    }
    int y=r;
    cout<<x-y+1<<endl;
}

Tokitsukaze and a+b=n (hard)

思路

tag :二分，容斥，哈希
B求两个区间，此题给了很多区间，有多少种选法，满足：从
m 个区间中选择两个区间 。
此时在我们面前的有两个问题：1.区间修改 2.找a=b-n
区间修改这里可以采用差分数组解决，那么a=b-n则用哈希表来解决
当我们枚举a时，判断有多少个b-n即可。
此时注意一个细节，我们这样寻找a->n-b，有可能a和b在一个区间的，这种情况怎么去除？我们可以将在同一个区间满足a=n-b的情况全部累加，再全部减去即可。

int n,m;
const int N=4e5+10;
int d[N];
const int mod=998244353;
int get(int l1,int r1,int l2,int r2)
{
    int l=l1-1,r=r1;
    while(l<r)
    {
        int mid=l+r+1>>1;
        if(n-mid>=l2)l=mid;
        else r=mid-1;
    }
    int x=l;
    l=l1,r=r1+1;
    while(l<r)
    {
        int mid=l+r>>1;
        if(n-mid<=r2)r=mid;
        else l=mid+1;
    }
    int y=r;
    return x-y+1;
}
void solve()
{
	cin>>n>>m;
	int s=0;
	rep(i,1,m)
	{
		int l,r;
		cin>>l>>r;
		s+=get(l,r,l,r);
		d[l]++,d[r+1]--;
	}
	int res=0;
	rep(i,1,N-1)d[i]+=d[i-1];
	rep(i,1,N-1)
	{
		if(n>=i)res=(res+d[i]*d[n-i]);
	}
	res=(res-s+mod)%mod;
	cout<<res<<endl;
}

D. Tokitsukaze and Energy Tree

思路

tag：贪心，dfs，bfs，树形DP
贪心的想，当一个大的权值点深度越深，则它被求sum的次数就越多，所以我们就往这个方向靠，求出每个点的深度，深度越深，则赋予其越大的权值，最后累加求和即可。

bfs

int n;
const int N=2e5+10;
int h[N],ne[N<<1],e[N<<1],idx;
int dep[N],w[N];
void add(int a,int b)
{
	e[idx]=b,ne[idx]=h[a],h[a]=idx++;
}
void bfs(int u)
{
	queue<int>q;
	q.push(u);
	dep[u]=1;
	while(q.size())
	{
		int sz=q.size();
		for(int i=0;i<sz;i++)
		{
			auto t=q.front();
			q.pop();
			for(int i=h[t];~i;i=ne[i])
			{
				int j=e[i];
				dep[j]=dep[t]+1;
				q.push(j);
			}
		}
	} 
}
void solve()
{
	memset(h,-1,sizeof h);
	cin>>n;
	rep(i,2,n)
	{
		int a;
		cin>>a;
		add(a,i);
	}
	rep(i,1,n)cin>>w[i];
	bfs(1);
	sort(w+1,w+1+n);
	sort(dep+1,dep+1+n);
	int res=0;
	rep(i,1,n)res+=dep[i]*w[i];
	cout<<res<<endl;
}

dfs

int n;
const int N=2e5+10;
int h[N],ne[N<<1],e[N<<1],idx;
int dep[N],w[N];
void add(int a,int b)
{
	e[idx]=b,ne[idx]=h[a],h[a]=idx++;
}
void dfs(int u,int fa)
{
	dep[u]=dep[fa]+1;
	for(int i=h[u];~i;i=ne[i])
	{
		int j=e[i];
		if(j==fa)continue;
		dfs(j,u);
	}
}
void solve()
{
	memset(h,-1,sizeof h);
	cin>>n;
	rep(i,2,n)
	{
		int a;
		cin>>a;
		add(a,i),add(i,a);
	}
	rep(i,1,n)cin>>w[i];
	dfs(1,0);
	sort(w+1,w+1+n);
	sort(dep+1,dep+1+n);
	int res=0;
	rep(i,1,n)res+=dep[i]*w[i];
	cout<<res<<endl;
}

E. Tokitsukaze and Energy Tree

思维

tag: 二分，数学，打表，找规律


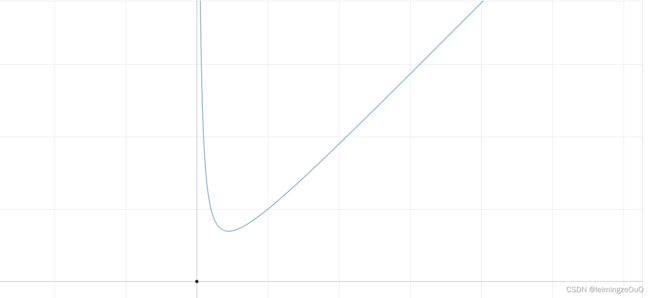
由绝对值不等式可知，函数最小值在$\sqrt{n}$处，由于题目所求的是最小正整数，所以设g(x)是f(x)取整的函数，函数图像

可知我们的函数值在整数点的邻域内是保持不变的，所以此题我们求最小值并不能采用三分写法。但是二分可以啊（傲娇。
由于我们给的是一个固定的区间，所以我们求的最小值无非L，R，$\sqrt{n}$,$\lceil \sqrt{n}\rceil$，四种情况，我们找到最小值的点，应该函数值相等的邻域的左端点，所以我们用求最小值的二分模板来解决

int l,r,n;
int f(int x)
{
    return n/x+x-1;
}
void solve()
{
    cin>>n>>l>>r;
    int sqrt_n=sqrtl(n);
    int f_l=f(l);
    int f_r=f(r);
    int pos=l,minv=f(l);
    if(f_l>f_r)
    {
        pos=r;
        minv=f(r);
    }
    if(sqrt_n>=l&&sqrt_n<=r&&minv>f(sqrt_n))
    {
        pos=sqrt_n;
        minv=f(sqrt_n);
    }
    sqrt_n++;
    if(sqrt_n>=l&&sqrt_n<=r&&minv>f(sqrt_n))
    {
        pos=sqrt_n;
        minv=f(sqrt_n);
    }
    int L=l,R=pos;
    while(L<R)
    {
        int mid=L+R>>1;
        if(f(mid)<=minv)R=mid;
        else L=mid+1;
    }
    cout<<R<<endl;
}

F. Tokitsukaze and Gold Coins (easy)

思路

tag:dfs，bfs，思维
求起点到终点最多可走多少格子，最简单的方法就是起点终点各跑一次bfs，然后找都可以做到的点。

const int N=5e5+10;
int n,k;
int g[N][4];
int st[N][4][2];
int dx[2][2],dy[2][2];
void bfs(PII start,bool f)
{
    queue<PII>q;
    q.push(start);
    if(f)st[start.x][start.y][f]=1;
    while(q.size())
    {
        auto t=q.front();
        q.pop();
        for(int i=0;i<2;i++)
        {
            int a=t.x+dx[i][f],b=t.y+dy[i][f];
            if(a<=0||a>n||b<=0||b>3)continue;
            if(g[a][b]==1)continue;
            if(st[a][b][f])continue;
            st[a][b][f]=1;
            q.push({a,b});
        }
    }
}
void solve()
{
    cin>>n>>k;
    dx[0][0]=0,dx[1][0]=1,dx[0][1]=0,dx[1][1]=-1;
    dy[0][0]=1,dy[1][0]=0,dy[0][1]=-1,dy[1][1]=0;
    rep(i,1,n)
        rep(j,1,3)g[i][j]=0;
    rep(i,1,n)
        rep(j,1,3)
            rep(k,0,1)st[i][j][k]=0;
    rep(i,1,k)
    {
        int x,y;
        cin>>x>>y;
        g[x][y]^=1;
    }
    bfs({1,1},0);
    bfs({n,3},1);
    int res=0;
    rep(i,1,n)
        rep(j,1,3)
            if(st[i][j][0]==st[i][j][1]&&st[i][j][0])res++;
    cout<<res<<endl;
}

G. Tokitsukaze and Gold Coins (hard)

待补。。。

H. Tokitsukaze and K-Sequence

思路

tag:哈希，差分，枚举，思维
我们发现，当前分成k组时，如果某种元素个数<=k，那么权值加上这一部分元素的个数，如果某种元素个数>k，则该种元素的造成的影响是k-1，累加即可。

int n;
const int N=1e5+10;
int a[N];
void solve()
{
	cin>>n;
	map<int,int>mp,mb;
	rep(i,1,n)cin>>a[i],mp[a[i]]++;
	for(auto x:mp)mb[x.y]++;
	vector<int>res(n+1,0);
	int s=mp.size();
	int cnt=0;
	rep(i,1,n)
	{
		s-=mb[i];
		res[i]+=(i-1)*s;
		cnt+=mb[i]*i;
		res[i]+=cnt;
	}
	rep(i,1,n)cout<<res[i]<<endl;
}

I. Tokitsukaze and Musynx

思路

tag: 贪心，哈希，容斥
贪心的想，总权值最大，可能存在一个点处于v的边界上，再看数据范围，因此我们可以枚举边界（即H），用map存一下分别对应的改变区间，最后，分别枚举不同的H求maxv即可。此题难点在于贪心的考虑H在v边界上最优。

int n,m;
const int N=2e5+10;
int x[N],a[5];
int v[10];
map<int,vector<int>>mp;
void solve()
{
	mp.clear();
	cin>>n;
	rep(i,1,n)cin>>x[i],x[i]-=1e8;
	rep(i,1,4)cin>>a[i];
	rep(i,1,5)cin>>v[i];
	rep(i,1,n)
	{
		rep(j,1,4)
		{
			mp[a[j]-x[i]+(j==4)].pb(-j);
			mp[a[j]-x[i]+(j==4)].pb(j+1);
		}
	}
	int res=v[1]*n;
	int maxv=res;
	for(auto x:mp)
	{
		for(auto y:x.y)
		{
			if(y>0)res+=v[y];
			else res-=v[-y];
		}
		maxv=max(res,maxv);
	}
	cout<< maxv<<endl;
}

J. Tokitsukaze and Sum of MxAb

思路

tag:思维
枚举每个$a_i$发现,枚举到i时，$res+=(n+1)\ast abs(a[i])$，之后每个循环，都加一个$abs(a[i])（n-1）次$，所以对于每个$a[i]，res+=2\ast n\ast abs(a[i])$。

int n;
const int N=1e5+10;
int a[N];
void solve()
{
    cin>>n;
    int res=0;
    rep(i,1,n)cin>>a[i];
    rep(i,1,n)res+=2*n*abs(a[i]);
    cout<<res<<endl;
}

K. Tokitsukaze and Synthesis and Traits

思路

tag：图论
给出的图是无向不连通图，题目实际要求给k个点，判断图中有多少个出现过。
我们可以将图转换成有向无环图，转换方法是：度少的->度多的，度一样，编号小的->编号大的。
然后暴力搜索一下即可，时间复杂度$\sqrt{m}$。

int n,m,q;
const int N=2e5+10;
int h[N],e[N<<1],ne[N<<1],idx;
int d[N];
int times[N];
vector<PII>edg;
void add(int a,int b)
{
	e[idx]=b,ne[idx]=h[a],h[a]=idx++;
}
void solve()
{
	cin>>n>>m>>q;
	memset(h,-1,sizeof h);
	rep(i,1,m)
	{
		int a,b;
		cin>>a>>b;
		d[a]++,d[b]++;
		edg.pb({a,b});	
	}
	rep(i,0,m-1)
	{
		int a=edg[i].x,b=edg[i].y;
		if(d[a]<d[b])add(a,b);
		else
		{
			if(d[a]>d[b])add(b,a);
			else
			{
				if(a<b)add(a,b);
				else add(b,a);
			}
		}
	}
	vector<int>vec;
	while(q--)
	{
		int k;
		cin>>k;vec.clear();
		rep(i,1,k)
		{
			int x;
			cin>>x;
			vec.pb(x);
			times[x]=1;
		}
		int res=0;
		rep(u,0,k-1)
		{
			for(int i=h[vec[u]];~i;i=ne[i])
			{
				int j=e[i];
				if(times[j])res++;
			}
		}
		cout<<res<<endl;
		for(auto x:vec)times[x]=0;
	}
}

L. Tokitsukaze and Three Integers

思路

tag： 容斥，哈希,预处理
这题思路不难，难在预处理上去重，定义f[i][j]：a或b选取v[i]时a*b（j）的个数。

int n,p;
const int N=5e3+10;
int a[N];
int f[N][N];
int cnt[N];
void solve()
{
	cin>>n>>p;
	rep(i,1,n)cin>>a[i];
	rep(i,1,n)
	{
		rep(j,1,n)
		{
			if(i==j)continue;
			cnt[a[i]%p*a[j]%p]++;
			f[i][a[i]%p*a[j]%p]+=2;
		}
	}
	rep(i,0,p-1)
	{
		int res=0;
		rep(j,1,n)
		{
			int t=a[j]%p;
			int v=(i-t+p)%p;
			res+=cnt[v]-f[j][v];
		}
		cout<<res<<' ';
	}
}