【算法练习】蓝桥杯C++ AB组辅导课题单：第三、四、五讲（Java解答版）

带※的题目，代表值得二刷、三刷、多刷！

一、数学与简单DP

※1205、买不到的数目（简单）（互质两数不能凑出的最大数）

类似于下面这道题：

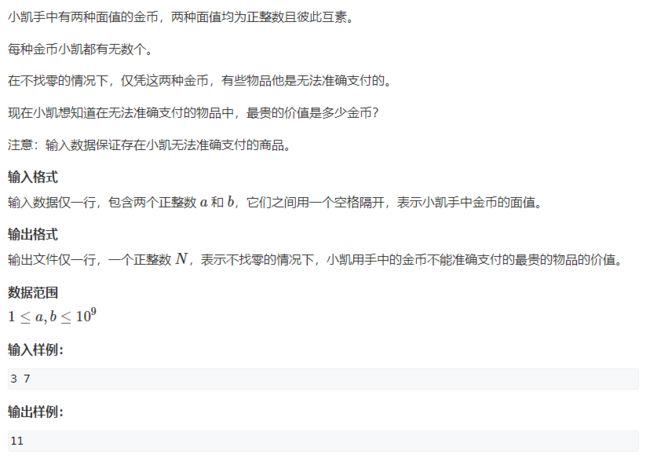
如果知道数学结论很快就可以得出答案：

也可以通过打表方式找规律。

import java.util.Scanner;

public class Main {
	public static void main(String[] args) {
		Scanner scan = new Scanner(System.in);
		long n = scan.nextLong();
		long m = scan.nextLong();
		System.out.println(n * m - n - m);
	}
}

同理，回到本题，跟上面一样的代码：

import java.util.Scanner;

public class Main {
	public static void main(String[] args) {
		Scanner scan = new Scanner(System.in);
		long n = scan.nextLong();
		long m = scan.nextLong();
		System.out.println(n * m - n - m);
	}
}

数论的题目只能多积累，因为涉及的东西太多了。

1211、蚂蚁感冒（简单）

对于感冒的蚂蚁，不管它向哪边走，如果它的左边有向右走的蚂蚁，或者它的右边有向左走的蚂蚁，它们都可能被感染。所以cnt = left + right + 1（left代表，感染蚂蚁的左边向右走的蚂蚁数，right代表，感染蚂蚁的右边向左走的蚂蚁数，+1是代表感染蚂蚁本身）。

上面的情况只是普遍情况，还要讨论特殊情况，例如：感冒的蚂蚁向左走，但是它左边没有向右的蚂蚁，或者感冒的蚂蚁向右走，但是它右边的蚂蚁没有向左的蚂蚁，那么都不能感染。

import java.util.Scanner;

public class Main {
	public static void main(String[] args) {
		Scanner scan = new Scanner(System.in);
		int n = scan.nextInt();
		int[] ants = new int[n];
		for (int i = 0; i < n; i++) {
			ants[i] = scan.nextInt();
		}
		// 如果第一个蚂蚁为负值，头朝左
		int left = 0;
		int right = 0;
		for (int i = 1; i < n; i++) {
			if (Math.abs(ants[i]) < Math.abs(ants[0])) {
				// 在左边,考虑头朝右
				if (ants[i] > 0) left++;
			} else {
				// 在右边,考虑头朝左
				if (ants[i] < 0) right++;
			}
		}
		// 考虑特殊情况
		if (ants[0] < 0 && left == 0) System.out.println(1);
		else if (ants[0] > 0 && right == 0) System.out.println(1);
		else System.out.println(left + right + 1);
	}
}

1216、饮料换购（简单）

直接模拟就行

import java.util.Scanner;

public class Main {
	public static void main(String[] args) {
		Scanner scan = new Scanner(System.in);
		int n = scan.nextInt();
		int ans = n;
		while (n >= 3) {
			// 剩下的瓶盖数
			int left = n % 3;
			// 换购
			ans += n / 3;
			n = n / 3 + left;
		}
		System.out.println(ans);
	}
}

2、01背包问题（简单）

经典中的经典

import java.util.Scanner;

public class Main {
	public static void main(String[] args) {
		Scanner scan = new Scanner(System.in);
		int n = scan.nextInt();
		int v = scan.nextInt();
		int[] vs = new int[n + 1];
		int[] ws = new int[n + 1];
		for (int i = 1; i <= n; i++) {
			vs[i] = scan.nextInt();
			ws[i] = scan.nextInt();
		}
		// n件物品，v容量的背包
		int[][] dp = new int[n + 1][v + 1];
		for (int i = 1; i <= n; i++) {
			for (int j = 1; j <= v; j++) {
				if (j >= vs[i]) {
					// 当前物品放得下
					dp[i][j] = Math.max(dp[i - 1][j], dp[i - 1][j - vs[i]] + ws[i]);
				} else {
					// 当前物品放不下
					dp[i][j] = dp[i - 1][j];
				}
			}
		}
		System.out.println(dp[n][v]);
	}
}

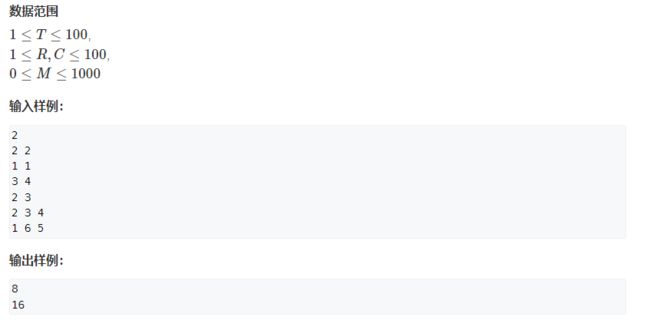
1015、摘花生（简单）

同样，经典中的经典！

import java.util.Scanner;

public class Main {
	public static void main(String[] args) {
		Scanner scan = new Scanner(System.in);
		int t = scan.nextInt();
		int[][] penuts;
		int[][] dp;
		while ((t--) > 0) {
			int r = scan.nextInt();
			int c = scan.nextInt();
			penuts = new int[r][c];
			for (int i = 0; i < r; i++) {
				for (int j = 0; j < c; j++) {
					penuts[i][j] = scan.nextInt();
				}
			}
			// 只能向东向南->向右向下
			dp = new int[r][c];
			dp[0][0] = penuts[0][0];
			// 初始化第一行
			for (int i = 1; i < c; i++) {
				dp[0][i] = dp[0][i - 1] + penuts[0][i];
			}
			// 初始化第一列
			for (int i = 1; i < r; i++) {
				dp[i][0] = dp[i - 1][0] + penuts[i][0];
			}
			for (int i = 1; i < r; i++) {
				for (int j = 1; j < c; j++) {
					dp[i][j] = Math.max(dp[i - 1][j], dp[i][j - 1]) + penuts[i][j];
				}
			}
			System.out.println(dp[r - 1][c - 1]);
		}
	}
}

895、最长上升子序列（简单）

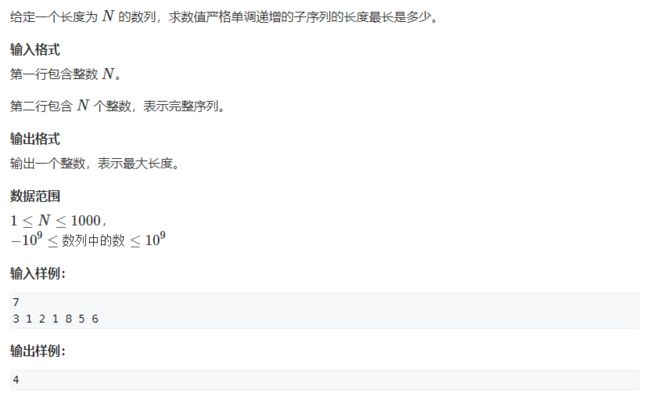
典中典！（可以看看LeetCode的这道题，描述的更详细，会告诉你什么叫做子序列）

import java.util.Scanner;

public class Main {
	public static void main(String[] args) {
		Scanner scan = new Scanner(System.in);
		int n = scan.nextInt();
		int[] nums = new int[n];
		for (int i = 0; i < n; i++) {
			nums[i] = scan.nextInt();
		}
		// dp[i] 以第i个数结尾的，严格递增的子序列的最大长度
		// 子序列：可以删除中间的某些数，但不能改变数的相对位置
		int[] dp = new int[n];
		dp[0] = 1;
		int ans = 1;
		for (int i = 1; i < n; i++) {
			dp[i] = 1;
			// 遍历i之前的数（因为按照dp定义，必须以i结尾）
			int max = 1;
			for (int j = 0; j <= i; j++) {
				if (nums[j] < nums[i]) {
					// + 1是代表必须以nums[i]结尾
					max = Math.max(dp[j] + 1, max);
				}
			}
			dp[i] = max;
			ans = Math.max(ans, dp[i]);
		}
		System.out.println(ans);
	}
}

※1212、地宫取宝（中等）（DP）

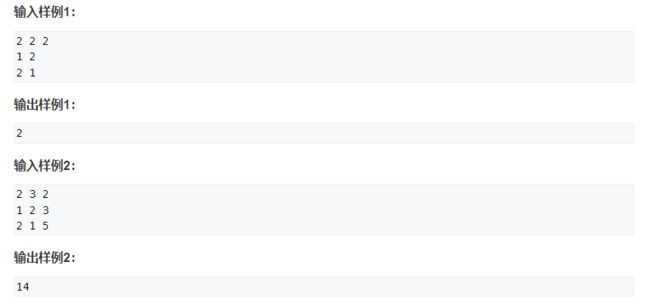
属于是上面两道题的升级版，贴一个y总分析法：

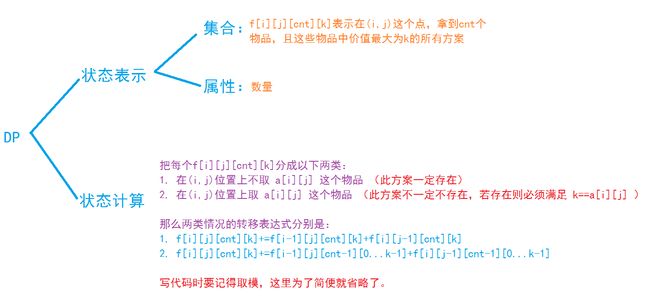
为什么取a[i][j]这个物品，必须要求k==a[i][j]呢？

因为根据题目要求，当前拿到的物品必须大于手中每个物品的价值，那当前取得的物品必须就是最大值，也就是k必须等于a[i][j]

import java.util.Scanner;

public class Main {
	static int MOD = 1000000007;
	public static void main(String[] args) {
		Scanner scan = new Scanner(System.in);
		int n = scan.nextInt();
		int m = scan.nextInt();
		int c = scan.nextInt();
		int[][] map = new int[n + 1][m + 1];
		int maxVal = 0;
		for (int i = 1; i <= n; i++) {
			for (int j = 1; j <= m; j++) {
				map[i][j] = scan.nextInt();
				// 由于宝贝价值可能为0，不方便判断是否拿宝贝，所以全部++
				map[i][j]++;
				// 求所有宝贝最大价值
				maxVal = Math.max(maxVal, map[i][j]);
			}
		}
		// 多了两个状态：手中宝贝数、手中物品最大价值，那就成了4维DP
		int[][][][] dp = new int[n + 1][m + 1][c + 1][maxVal + 1];
		// dp[i][j][cnt][val]，在i,j位置，手中持有cnt件物品，其中最大价值为val的方案数
		
		// 第一个位置有两种情况，拿、不拿
		dp[1][1][0][0] = 1;
		dp[1][1][1][map[1][1]] = 1;
		// 枚举所有情况
		for (int i = 1; i <= n; i++) {
			for (int j = 1; j <= m; j++) {
				for (int cnt = 0; cnt <= c; cnt++) {
					// 枚举拿cnt件物品
					for (int k = 0; k <= maxVal; k++) {
						// 枚举最大价值
						// 不拿，它只能从左边或上边转移过来
					
						// 写上加自身是因为dp[1][1][0][0]本身是有值的，并不是=0的
						// 而又无法避免cnt必须从0开始遍历，所以只能是自加
						dp[i][j][cnt][k] = (dp[i][j][cnt][k] + dp[i - 1][j][cnt][k]) % MOD;
						dp[i][j][cnt][k] = (dp[i][j][cnt][k] + dp[i][j - 1][cnt][k]) % MOD;
					
						// 拿商品，那cnt必须 >0，且最大价值k就是当前物品自身
						if (cnt > 0 && k == map[i][j]) {
							// 遍历所有之前可能的最大价值，都可能转移过来
							for (int s = 0; s < map[i][j]; s++) {
								dp[i][j][cnt][k] = (dp[i][j][cnt][k] + dp[i - 1][j][cnt - 1][s]) % MOD;
								dp[i][j][cnt][k] = (dp[i][j][cnt][k] + dp[i][j - 1][cnt - 1][s]) % MOD;
							}
						}
					}
				}
			}
		}
		
		// 最后统计所有拿了c个物品的，但物品的最大价值不确定的所有方案数
		int res = 0;
		for (int i = 1; i <= maxVal; i++) {
			res = (res + dp[n][m][c][i]) % MOD;
		}
		System.out.println(res);
	}
}

※1214、波动数列（中等）（DP）

DP永远的坎…连续两道DP，我心态崩了…

扩展知识：负余数转正余数

int getMod(int a, int b) {
	return (a % b + b) % b;
}

最不好理解的就是这里的转换：x为任意整数，所以得出，第一个数s，与后面n-1个数根据a、b操作组成的序列和模n的余数相同。

上面的转移方程还不够，因为我们要找与第一个数s同余，且长度为n-1的方案数，所以对j + b(n-i)、j - a(n-i)都要对n取余，因为题目中的数据可能为负数，但是数组index没法为负，就需要把负余数转成正余数，就是用上面的方法。最终答案就是：f[n - 1][s % n]，当然这里的s % n也得用正余数。

import java.util.Scanner;

public class Main {
	static int MOD = 100000007;
	static int getMod(int a, int b) {
		return (a % b + b) % b;
	}
	public static void main(String[] args) {
		Scanner scan = new Scanner(System.in);
		int n = scan.nextInt();
		int s = scan.nextInt();
		int a = scan.nextInt();
		int b = scan.nextInt();
		int[][] dp = new int[n][n];
		// dp[i][j]选了i个数，前 i 个 d 的和模 n 的余数为 j 的集合的数量
		// 这个d可以是+a、-b
		dp[0][0] = 1;
		// 一个数没选，模n为0的方案数=1
		for (int i = 1; i < n; i++) {
			for (int j = 0; j < n; j++) {
				dp[i][j] = (dp[i - 1][getMod(j + b * (n - i), n)] + dp[i - 1][getMod(j - a * (n - i), n)]) % MOD;
			}
		}
		System.out.println(dp[n - 1][getMod(s, n)]);
	}
}

---

二、枚举、模拟与排序

这类题目是非常值得练手的题目，可以帮助自己写代码的时候更加细心仔细

1210、连号区间数（简单）

注意要满足长度为R-L+1的连续数列，也就是说：最大值-最小值，等于左右下标之差，抓住这个关键信息就可以很快拿下。

import java.util.*;

public class Main {
    public static void main(String[] args) {
    	Scanner scan = new Scanner(System.in);
    	int n = scan.nextInt();
    	int[] num = new int[n];
    	for (int i = 0; i < n; i++) {
    		num[i] = scan.nextInt();
    	}
    	// 每个数字和自己都可以组成
    	int ans = n;
    	for (int i = 0; i < n; i++) {
    		int max = num[i];
    		int min = num[i];
    		for (int j = i + 1; j < n; j++) {
    			max = Math.max(max, num[j]);
    			min = Math.min(min, num[j]);
    			if (max - min == j - i) ans++;
    		}
    	}
    	System.out.println(ans);
    }
}

1236、递增三元组（中等）

我们去枚举中间数，找A数组中有多少数小于当前数，找B数组中有多少数大于当前数即可。

import java.util.*;

public class Main {
    public static void main(String[] args) {
    	Scanner scan = new Scanner(System.in);
    	int n = scan.nextInt();
    	int[] A = new int[n];
    	int[] B = new int[n];
    	int[] C = new int[n];
    	for (int i = 0; i < n; i++) A[i] = scan.nextInt();
    	for (int i = 0; i < n; i++) B[i] = scan.nextInt();
    	for (int i = 0; i < n; i++) C[i] = scan.nextInt();
    	long ans = 0;
    	int p = 0, q = 0;
    	// 需要注意，排序并不改变最终结果
    	Arrays.sort(A);
    	Arrays.sort(B);
    	Arrays.sort(C);
    	for (int i = 0; i < n; i++) {
    		// 找A前面有多少数小于Bi
    		while (p < n && A[p] < B[i]) p++;
    		// 找B后面第一个大于Bi的位置，这样后面大于Bi的数就有n - q
    		while (q < n && C[q] <= B[i]) q++;
    		ans += (long)(p * (n - q));
    	}
    	System.out.println(ans);
    }
}

1245、特别数的和（简单）

纯真的模拟，极致的体验

import java.util.*;

public class Main {
    public static void main(String[] args) {
    	Scanner scan = new Scanner(System.in);
    	int n = scan.nextInt();
    	long ans = 0;
    	for (int i = 1; i <= n; i++) {
    		if (check(i)) ans += i;
    	}
    	System.out.println(ans);
    }
    static boolean check(int x) {
    	while (x != 0) {
    		int t = x % 10;
    		x /= 10;
    		if (t == 2 || t == 0 || t == 1 || t == 9) return true;
    	}
    	return false;
    }
}

1204、错误票据（简单）

排序找重，找缺失值

import java.io.BufferedReader;
import java.io.IOException;
import java.io.InputStreamReader;
import java.util.*;

public class Main {
    static BufferedReader reader = new BufferedReader(new InputStreamReader(System.in));
	public static void main(String[] args) throws IOException {
		String[] input = reader.readLine().trim().split(" ");
		int n = Integer.parseInt(input[0]);
		int[] id = new int[10010];
		int idx = 0;
		while (n-- > 0) {
			input = reader.readLine().trim().split(" ");
			int len = input.length;
			for (int i = 0; i < len; i++) {
				id[idx++] = Integer.parseInt(input[i]);
			}
		}
		Arrays.sort(id, 0, idx);
		int mm = -1;
		int nn = -1;
		for (int i = 0; i < idx; i++) {
			if (i > 0 && id[i] == id[i - 1]) {
				// 重号
				nn = id[i];
			} else if (i > 0 && id[i] != id[i - 1] + 1){
				mm = id[i - 1] + 1;  // 缺号
			}
		}
		System.out.println(mm + " " + nn);
	}
}

466、回文日期（简单）

极致模拟，奢华体验

import java.io.*;
import java.util.*;

import javax.swing.text.AbstractDocument.LeafElement;

public class Main {
    static BufferedReader reader = new BufferedReader(new InputStreamReader(System.in));
	public static void main(String[] args) throws IOException {
		Scanner scan = new Scanner(System.in);
		int n = scan.nextInt();
		int year = n / 10000;
		int day = n % 100;
		int month = (n - year * 10000) / 100;
		// 先找下一个回文日期，再找下一个ABABBABA型回文日期
		// 如果闰年2月再加1天
		int[] M = new int[] {0, 31, 28, 31, 30, 31, 30, 31, 31, 30, 31, 30, 31};
		boolean flag1 = false;
		boolean flag2 = false;
		String ans1 = "";
		String ans2 = "";
		while (true) {
			// 从day开始更新日期
			day++;
			if (month == 2) {
				if (isLeap(year) && day > 29) {
					month++;
					day = 1;
				}
				if (!isLeap(year) && day > 28) {
					month++;
					day = 1;
				}
			} else {
				if (day > M[month]) {
					month++;
					day = 1;
				}
			}
			if (month > 12) {
				month = 1;
				year++;
			}
			StringBuilder sb = new StringBuilder();
			sb.append(year);
			if (month < 10) {
				sb.append(0).append(month);
			} else {
				sb.append(month);
			}
			if (day < 10) {
				sb.append(0).append(day);
			} else {
				sb.append(day);
			}
			if (check(sb.toString()) && flag1 == false) {
				flag1 = true;
				ans1 = sb.toString();
			}
			if (check1(sb.toString()) && flag2 == false) {
				flag2 = true;
				ans2 = sb.toString();
			}
			// 两个都找到了在输出
			if (flag1 && flag2) break;
		}
		System.out.println(ans1);
		System.out.println(ans2);
	}
	// 判断闰年
	static boolean isLeap(int year) {
		if ((year % 4 == 0 && year % 100 != 0) || year % 400 == 0) return true;
		return false;
	}
	// 判断普通回文日期
	static boolean check(String str) {
		int i = 0;
		int j = str.length() - 1;
		while (i <= j) {
			if (str.charAt(i) != str.charAt(j)) return false;
			i++;
			j--;
		}
		return true;
	}
	// 判断ABABBABA型回文日期
	static boolean check1(String str) {
		char A = str.charAt(0);
		char B = str.charAt(1);
		if (str.charAt(2) == A && str.charAt(3) == B && str.charAt(4) == B && str.charAt(5) == A && str.charAt(6) == B && str.charAt(7) == A) {
			return true;
		}
		return false;
	}
}

787、归并排序（简单）

实现归并排序

import java.io.*;
import java.util.*;

public class Main {
    static BufferedReader reader = new BufferedReader(new InputStreamReader(System.in));
	public static void main(String[] args) throws IOException {
		Scanner scan = new Scanner(System.in);
		int n = scan.nextInt();
		int[] nums = new int[n];
		for (int i = 0; i < n; i++) nums[i] = scan.nextInt();
		// 辅助数组
		int[] tmp = new int[n];
		mergeSort(nums, tmp, 0, n - 1);
		System.out.println(Arrays.toString(nums));
	}
	static void mergeSort(int[] nums, int[] tmp, int left, int right) {
		if (left < right) {
			int mid = left + (right - left) / 2;
			mergeSort(nums, tmp, left, mid);
			mergeSort(nums, tmp, mid + 1, right);
			merge(nums, tmp, left, mid, right);
		}
	}
	static void merge(int[] nums, int[] tmp, int left, int mid, int right) {
		int i = left;
		int j = mid + 1;
		int k = 0;
		// i是前半部分数组的开始下标，j是后半部分数组的开始下表，k是新的数组的下标
		while (i <= mid && j <= right) {
			if (nums[i] <= nums[j]) {
				// 用<=保证排序的稳定性
				tmp[k++] = nums[i++];
			} else {
				tmp[k++] = nums[j++];
			}
		}
		// 可能前一半数组没放完，也可能后一半数组没放完
		while (i <= mid) {
			tmp[k++] = nums[i++];
		}
		while (j < mid) {
			tmp[k++] = nums[j++];
		}
		// 将tmp中数组元素合并到nums
		for (int t = 0; t < k; t++) {
			nums[t + left] = tmp[t];
		}
	}
}

1219、移动距离（简单）

模拟坐标生成过程，计算曼哈顿距离即可。

import java.io.*;
import java.util.*;

public class Main {
    static BufferedReader reader = new BufferedReader(new InputStreamReader(System.in));
	public static void main(String[] args) throws IOException {
		Scanner scan = new Scanner(System.in);
		int w = scan.nextInt();
		int m = scan.nextInt();
		int n = scan.nextInt();
		m--;n--;
		int x1 = m / w;
		int x2 = n / w;
		int y1 = m % w;
		int y2 = n % w;
		if (x1 % 2 == 1) {
			// 如果是奇数行
			y1 = w - y1 - 1;
		} 
		if (x2 % 2 == 1) {
			// 如果是奇数行
			y2 = w - y2 - 1;
		}
		System.out.println(Math.abs(x1 - x2) + Math.abs(y1 - y2));
	}
}

1229、日期问题（简单）

极致模拟，纯真享受，丝滑体验

import java.io.*;
import java.util.*;

public class Main {
    static BufferedReader reader = new BufferedReader(new InputStreamReader(System.in));
	public static void main(String[] args) throws IOException {
		String[] input = reader.readLine().trim().split("/");
		// 年月日 月日年 日月年，年份忽略了前两位
		// 保证每次取出来都是年月日
		int[] date = new int[3];
		for (int i = 0; i < 3; i++) {
			date[i] = Integer.parseInt(input[i]);
		}
		int[][] chance = new int[][] {{0,1,2},{2,0,1},{2,1,0}};
		int[] M = new int[] {0,31,28,31,30,31,30,31,31,30,31,30,31};
		List<String> ans = new LinkedList<>();
		for (int i = 0; i < 3; i++) {
			int year = date[chance[i][0]];
			int month = date[chance[i][1]];
			int day = date[chance[i][2]];
			StringBuilder sb = new StringBuilder();
			if (year <= 59) {
				if (year < 10) {
					sb.append("200").append(year);
				} else {
					sb.append("20").append(year);
				}
			} else {
				sb.append("19").append(year);
			}
			if (month < 1 || month > 12) continue;
			if (month < 10) sb.append("-0").append(month);
			else sb.append("-" + month);
			if (day < 1) continue;
			int t = 0;
			if (isLeap(year)) {
				if (month == 2) t = 29;
				else t = M[month];
			} else {
				t = M[month];
			}
			if (day > t) continue;
			if (day < 10) sb.append("-0").append(day);
			else sb.append("-" + day);
			ans.add(sb.toString());
		}
		Collections.sort(ans);
		// 结果可能有重复，要去重
		for (int i = 0; i < ans.size(); i++) {
			if (i > 0 && ans.get(i).equals(ans.get(i - 1))) continue;
			System.out.println(ans.get(i));
		}
	}
	static boolean isLeap(int year) {
		if ((year % 4 == 0 && year % 100 != 0) || year % 400 == 0) {
			return true;
		}
		return false;
	}
}

1231、航班时间（简单）

因为不知道时差是多少，只知道在出发地的出发时间，已经目标地的到达时间，我们可以将两次的空中飞行时间相加再求平均值，最终结果就是答案。

图源：https://blog.csdn.net/Cyril_KI/article/details/107372908?spm=1001.2101.3001.6650.2&utm_medium=distribute.pc_relevant.none-task-blog-2%7Edefault%7ECTRLIST%7ERate-2.pc_relevant_antiscanv2&depth_1-utm_source=distribute.pc_relevant.none-task-blog-2%7Edefault%7ECTRLIST%7ERate-2.pc_relevant_antiscanv2&utm_relevant_index=5

转换成秒之后再去算时间差更方便

import java.io.*;
import java.util.*;

public class Main {
    static BufferedReader reader = new BufferedReader(new InputStreamReader(System.in));
	public static void main(String[] args) throws IOException {
		int t = Integer.parseInt(reader.readLine().trim().split(" ")[0]);
		while (t-- > 0) {
			String[] go = reader.readLine().trim().split(" ");
			String[] back = reader.readLine().trim().split(" ");
			int len = go.length;
			// 把起程时间转成秒
			String[] tmp = go[0].split(":");
			int start = Integer.parseInt(tmp[0]) * 3600 + Integer.parseInt(tmp[1]) * 60 + Integer.parseInt(tmp[2]);
			int aver = 0;
			int end = 0;
			tmp = go[1].split(":");
			end = Integer.parseInt(tmp[0]) * 3600 + Integer.parseInt(tmp[1]) * 60 + Integer.parseInt(tmp[2]);
			if (len == 3) {
				// 有 +1、+2
				int num = go[2].charAt(2) - '0';
				if (num == 1) {
					end += 24 * 3600;
				} else {
					end += 48 * 3600;
				}
			}
			aver = end - start;
			// 再来看回程时间
			len = back.length;
			tmp = back[0].split(":");
			start = Integer.parseInt(tmp[0]) * 3600 + Integer.parseInt(tmp[1]) * 60 + Integer.parseInt(tmp[2]);
			tmp = back[1].split(":");
			end = Integer.parseInt(tmp[0]) * 3600 + Integer.parseInt(tmp[1]) * 60 + Integer.parseInt(tmp[2]);
			if (len == 3) {
				// 有 +1、+2
				int num = back[2].charAt(2) - '0';
				if (num == 1) {
					end += 24 * 3600;
				} else {
					end += 48 * 3600;
				}
			}
			aver += end - start;
			aver /= 2;
			int second = aver % 60;
			int min = aver / 60 % 60;
			int hour = aver / 3600;
			StringBuilder sb = new StringBuilder();
			if (hour < 10) {
				sb.append("0").append(hour);
			} else {
				sb.append(hour);
			}
			if (min < 10) {
				sb.append(":0").append(min);
			} else {
				sb.append(":" + min);
			}
			if (second < 10) {
				sb.append(":0").append(second);
			} else {
				sb.append(":" + second);
			}
			System.out.println(sb.toString());
		}
	}
}

1241、外卖店优先级（简单）

记录每个id对应的订单时间即可，然后枚举每一个id，判断当前id是否能够在T时刻进入优先缓存。

import java.io.*;
import java.util.*;

public class Main {
    static BufferedReader reader = new BufferedReader(new InputStreamReader(System.in));
	public static void main(String[] args) throws IOException {
		String[] input = reader.readLine().trim().split(" ");
		int n = Integer.parseInt(input[0]);
		int m = Integer.parseInt(input[1]);
		int t = Integer.parseInt(input[2]);
		// n家外卖店，m条订单信息，计算t时刻有多少外卖店在优先缓存中
		HashMap<Integer, LinkedList<Integer>> map = new HashMap<>();
		int[] ids = new int[m];
		for (int i = 0; i < m; i++) {
			input = reader.readLine().trim().split(" ");
			int ts = Integer.parseInt(input[0]);
			int id = Integer.parseInt(input[1]);
			ids[i] = id;
			if (!map.containsKey(id)) {
				LinkedList<Integer> tmp = new LinkedList<>();
				tmp.add(ts);
				map.put(id, tmp);
			} else {
				LinkedList<Integer> tmp = map.get(id);
				tmp.add(ts);
				map.put(id, tmp);
			}
		}
		// 对id排序方便去重
		Arrays.sort(ids);
		int ans = 0;
		// 先遍历id，再遍历id对应的订单时间
		for (int i = 0; i < m; i++) {
			// id去重
			if (i > 0 && ids[i - 1] == ids[i]) continue;
			int id = ids[i];
			LinkedList<Integer> time = map.get(id);
			int[] cnt = new int[t + 1];
			for (int cur : time) {
				cnt[cur]++;  // 当前时间的订单数+1
			}
			int prior = 0;
			boolean flag = false;
			// 遍历所有时间的订单数，时间从1开始
			for (int j = 1; j <= t; j++) {
				if (cnt[j] == 0) {
					if (prior > 0) prior--;
				} else {
					prior += 2 * cnt[j];
				}
				if (prior > 5) flag = true;
				if (prior <= 3) flag = false;
			}
			// 在优先缓存中
			if (flag) ans++;
		}
		System.out.println(ans);
	}
}

788、逆序对的数量（简单）

是归并排序的扩展题目，在归并排序的过程中实现逆序对数量的统计。

import java.io.*;
import java.util.*;

public class Main {
    static BufferedReader reader = new BufferedReader(new InputStreamReader(System.in));
	static int ans = 0;  // 统计逆序对数量
    public static void main(String[] args) throws IOException {
		Scanner scan = new Scanner(System.in);
		int n = scan.nextInt();
		int[] nums = new int[n];
		for (int i = 0; i < n; i++) nums[i] = scan.nextInt();
		int[] tmp = new int[n];
		mergeSort(nums, tmp, 0, n - 1);
		System.out.println(Arrays.toString(nums));
		System.out.println(ans);
	}
	static void mergeSort(int[] nums, int[] tmp, int left, int right) {
		if (left < right) {
			int mid = left + (right - left) / 2;
			mergeSort(nums, tmp, left, mid);;
			mergeSort(nums, tmp, mid + 1, right);
			merge(nums, tmp, left, mid, right);
		}
	}
	static void merge(int[] nums, int[] tmp, int left, int mid, int right) {
		// 前半部分的开始下标，右半部分的开始下标，辅助数组的下标
		int i = left;
		int j = mid + 1;
		int k = 0;
		while (i <= mid && j <= right) {
			if (nums[i] <= nums[j]) {
				// 前半部分的值<=后半部分的值，不存在逆序对
				tmp[k++] = nums[i++];
			} else {
				// 此时出现了逆序对，nums[i] > nums[j]，说明i后面到mid的数都大于nums[j]
				ans += mid - i + 1;
				tmp[k++] = nums[j++];
			}
		}
		// 单独剩下的情况就不存在逆序对，前面已经统计过
		while (i <= mid) {
			tmp[k++] = nums[i++];
		}
		while (j <= right) {
			tmp[k++] = nums[j++];
		}
		// 把合并结果恢复到nums
		for (int t = 0; t < k; t++) {
			nums[t + left] = tmp[t];
		}
	}
}

1237、螺旋折线（中等）

先模拟找规律，然后再用规律去替换。

import java.util.*;

public class Main {
    public static void main(String[] args) {
        Scanner scan = new Scanner(System.in);
        long x = scan.nextLong();
        long y = scan.nextLong();
        // 对于整点(X, Y)，我们定义它到原点的距离dis(X, Y)是
        // 从原点到(X, Y)的螺旋折线段的长度
        long cnt = 0;
        if (x >= 0 && y >= 0) {
            // 第一象限
            if (y >= x) {
                // 2,3
                cnt = y * y * 4;
                cnt = cnt - (y - x);
            } else {
                // 3,2
                cnt = x * x * 4;
                cnt = cnt + (x - y);
            }
        } else if (x >= 0 && y <= 0) {
            // 第四象限
            if (-y >= x) {
                // 2,-3
                // 转换成上面的情况
                cnt = (-y) * (-y) * 4;
                cnt = cnt + (-y) * 2;
                cnt = cnt + (-y - x);
            } else {
                // 3,-2
                cnt = x * x * 4;
                cnt = cnt + x * 2;
                cnt = cnt - (x + y);
            }
        } else if (x <= 0 && y >= 0) {
            // 第二象限
            if (-x >= y) {
                // -3,2
                cnt = (-x) * (-x) * 4;
                cnt = cnt - (-x) * 2;
                cnt = cnt - (-x - y);
            } else {
                // -2,3
                cnt = y * y * 4;
                cnt = cnt - y * 2;
                cnt = cnt + (y + x);
            }
        } else if (x <= 0 && y <= 0) {
            // 第三象限
            if (-x >= -y) {
                // -3,-2
                cnt = (-y) * (-y) * 4;
                cnt = cnt + 4 * (-y);
                cnt = cnt + (y - x);
            } else {
                // -2,-3
                cnt = (-y) * (-y) * 4;
                cnt = cnt + 4 * (-y);
                cnt = cnt - (x - y);
            }
        }
        System.out.println(cnt);
    }
}

三、树状数组与线段树

这一讲的练习，都放在了树状数组、差分专题中，详情可点击链接。这一讲主要需要掌握：树状数组使用、差分多维数组（矩阵）、前缀和多维数组（矩阵）

1264、动态求连续区间和（简单）

1265、数星星（中等）

1270、数列区间最大值（简单）

1215、小朋友排队（简单）

1228、油漆面积（困难）

※※1232、三体攻击（困难）

797、差分（简单）

※798、差分矩阵（简单）