Acwing 1228. 油漆面积（线段树+扫描线）

 

 解题思路：给定一个矩形，将矩形的左右两条边所在的直线进行延长，对整个区域进行划分，这就是扫描线名字的由来，每一条扫描线都是一颗线段树，它与一般有懒标记的线段树有一下几个区别：

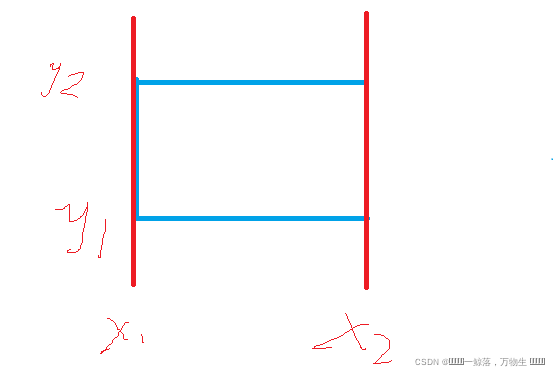
1、扫描线中每个点代表的是一个线段，具体到这个题中就是每次给我们一个矩形的信息，我们可以对它构建出一个三元组（x1,y1,y2)，(x2,y1,y2),如下图所示

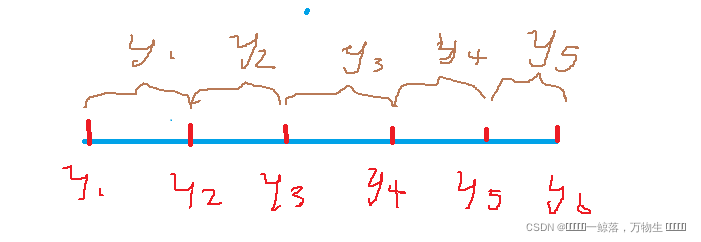
其中记录x的作用是用来确定当前扫描线被计算的顺序的，y1,y2可以用来表示当前的那一段要进行覆盖，在x1处要对[y1,y2-1]这一段的覆盖次数加一，表示被覆盖，在x2处减一，解除覆盖，注意这里为什么是y2-1,前面说过这里的点代表的是实际中的线段，可以通过下面的图来理解

给定的是点的标号，也就是图上下面的y1,y2，而我们写代码用到的是上面的表示线段的的y1,y2

2、标记不会向下更新，当更新到当前线段树时如果刚好包括当前节点的所表示的一段，那对当前节点更新后，就不会向下更新，为啥？，因为我们最终需要的答案始终是由根节点提供的，当前节点更新后，只需要向上层节点回溯到根节点即可，不必向下更新。

做法就是先根据x坐标对得到的三元组进行排序，更新答案（答案加上根节点中被覆盖的区间长度*当前2条扫描线之间的宽度），然后进行上面第1点提到的操作。

上代码：

#include 
#include 
#include 
#include 
using namespace std;
const int N =1e4+10;
struct segment{
    int x,y1,y2;
    int k;
    bool operator < (const segment& t)const 
    {
        return x0)
    tr[rt].len=tr[rt].r-tr[rt].l+1;
    else if(tr[rt].l==tr[rt].r)
    tr[rt].len=0;
    else
    tr[rt].len=tr[rt<<1].len+tr[rt<<1|1].len;
}
void build(int rt,int l,int r)
{
    tr[rt]={l,r};
    if(l==r)
    return ;
    int mid=l+r>>1;
    build(rt<<1,l,mid);
    build(rt<<1|1,mid+1,r);
}
void modify(int rt,int l,int r,int k)
{
    if(tr[rt].l>=l&&tr[rt].r<=r)
    {
        tr[rt].cnt+=k;
        pushup(rt);
    }
    else
    {
        int mid=tr[rt].l+tr[rt].r>>1;
        if(l<=mid)
        modify(rt<<1,l,r,k);
        if(r>mid)
        modify(rt<<1|1,l,r,k);
        pushup(rt);
    }
}
int main()
{
    cin>>n;
    for(int i=1;i<=n;i++)
    {
        int x1,y1,x2,y2;
        cin>>x1>>y1>>x2>>y2;
        seg[m++]={x1,y1,y2,1};
        seg[m++]={x2,y1,y2,-1};
    }
    sort(seg,seg+m);
    build(1,0,10000);
    int res=0;
    for(int i=0;i0)
        res+=tr[1].len*(seg[i].x-seg[i-1].x);
        modify(1,seg[i].y1,seg[i].y2-1,seg[i].k);
    }
    cout<