ChatGPT原理解读

GPT痛点

GPT作为一个通用大数据训练的生成式语言模型，对于输入的prompt，它的回答往往不见得是我们希望的，可能只是它之前在海量网络页面上“看”到过的一个相关，但无用，甚至是“有毒”的内容。例如：

• 我们的提问是： ACL会议的主题是什么？
• 期待的回答是：ACL的会议主题是自然语言处理，包括自然语言生成，自然语言理解，…
• 但GPT的回答可能是：ACL的会议地址在XXX，时间是XXX，… (相关但无用的回答)

因此如何让GPT的输出更靠近我们希望的回答方向，是使得GPT成为真正具有“智能”的AI工具的主要困难。

---

基于人类反馈的强化学习机制（ChatGPT）

ChatGPT的流程图如下：

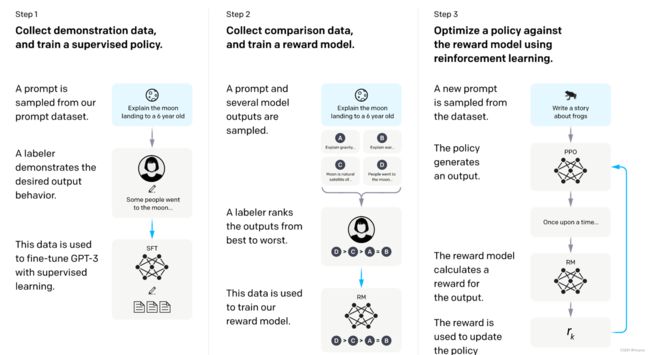
step1：Fine-tune SFT模型

研究人员首先准备了一些 “prompt + 人工回答” 作为训练数据喂给了 GPT-3 模型，通过fine-tune得到SFT模型，这一步总共用到了13K的prompt数据

---

step2：训练Reward模型

第二步就比较关键了，这里说一句，其实想让GPT-3变成一个“听话”的模型，也可以直接通过利用 “prompt + 人工回答” 给它做微调来实现。但一方面，人工prompt和回答是很贵的，另一方面，可能需要非常多这样的人工数据才可以把模型微调好。

所以这里的Reward模型可以认为是我们造的一个“人工标注机”，我们希望它的偏好尽量靠近人的偏好；换句话说，只有当GPT给出的回答是人类希望的回答时，Reward模型才会对这个回答给出高分。

Reward模型的结构也非常简单，只需要将上面的SFT模型拿来，将最后一层embedding层换成一维线性输出层。然后把 prompt+回答A 输入到Reward模型，输出的一维标量，就是“回答A”相对于这个prompt的得分了。

有了模型结构，ChatGPT是怎么构造Reward模型的损失函数的呢？

这里也非常巧妙，研究人员首先给了一些prompt，对于每个promt，让SFT生成N个回答。这里可以把prompt记为 $x$，把这N个生成的回答记为 $\{y_1,y_2,\cdots ,y_N\}$。他们首先让人工标记员将这N个回答进行排序，从这个排序中就可以获得这N个回答两两之间的对比。比如：$y_1好于y_2$，那么我们构造的损失函数就希望 $y_1$ 在Reward模型的得分也尽量比 $y_2$高，由此，论文中给出的损失函数公式如下：

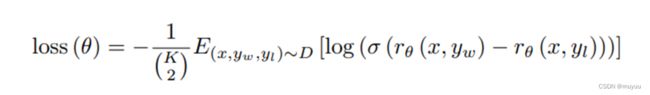
其中 $E_{(x,y_w,y_l)\sim D}[log(\cdot )]$是cross-entropy，根据我们在 最大似然估计与交叉熵对交叉熵的介绍来看，这里是希望 $\sigma (r_{\theta }(x,y_w)-r_{\theta }(x,y_l))$ 尽量与真实的 $(x,y_w,y_l)$ 的情况一致。这里面用到的sigmoid函数一般是用来做二分类的。所以这里其实是将排序问题转化成二分类问题：

• $y_w$ 好于 $y_l$ 时：
  $$Obj:\sigma (r_{\theta }(x,y_w)-r_{\theta }(x,y_l))\to 1$$
• $y_w$ 坏于 $y_l$ 时：
  $$Obj:\sigma (r_{\theta }(x,y_w)-r_{\theta }(x,y_l))\to -1$$

论文还提到，也可以只选出最好的结果，然后将它与剩下的N-1个回答做对比。但实验显示，这样由于数据量少且有冗余性，模型很容易就overfit了。换成两两对比之后，就不容易出现这样的问题了

---

step3：强化学习训练PPO模型

PPO模型初始化也是基于上面的SFT模型，它的目标是微调SFT模型，使得微调过后的PPO模型生成的回答，在Reward模型上的得分尽量高。再结合我们上面训练的Reward模型的目标是使得它的偏好尽量靠近人的偏好，所以这里我们训得的PPO模型就是最开始想得到的“智能”模型。

这里用到了强化学习中的PPO(Proximal Policy Optimization)近端策略优化算法。众所周知，强化学习是一种根据实时反馈来优化策略的一种学习方法，我们上面训练得到的Reward模型就是在这里提供实时反馈的模型，优化目标如下：

这里第一项 $r_{\theta }(x,y)$ 很好理解，就是我们希望模型生成的结果 $(x,y)$ 在Reward模型的得分尽量高。第二部分是当前模型和初始SFT模型的KL散度，那么为什么会有这一项呢？

这里我们要简单说一下强化学习中的 on-Policy 与 off-Policy：

• on-Policy：每次使用的 $(x,y)$ 都是当前模型生成的结果
  缺点：更新速度慢，而且如果模型的训练出现了问题，那么采集到的数据也不好，会陷入恶性循环。
• off-Policy：从初始模型拿到 $(x,y)$ 后，每次更新模型都用这批数据
  优点：更新速度快，保证数据质量不会飘移

因为强化学习需要的是实时反馈，所以理想情况，我们是想用on-Policy策略的，但由于on-Policy策略有如上种种缺点，因此在PPO算法中，实际使用的是off-Policy策略。这里假设当前模型可以用分布$p(x)$表示，初始模型用分布$q(x)$表示，那么根据下图推导：

当我们将策略从 on-Policy 转为 off-Policy，想要保持优化目标不随之改变太多，就要求 $q(x)$ 尽量靠近 $p(x)$。而KL散度正是衡量两个分布之间的差距的，因此需要在loss func中减去这一项，以使得 off-Policy 策略有效。

loss func中的第三项是加上了原始预训练LM模型的目标函数，这是因为如果只有对$r_{\theta }(x,y)$的约束，那么极端情况下，找到的 $\theta$ 可以是使得生成的任意 $y$ 都满足 $r_{\theta }(x,y)$ 尽量大的 $\theta$，而这样生成的 $y$ 可能是没有意义的句子，甚至是乱码

---

到这里就介绍完了ChatGPT的算法思路。可以看出ChatGPT能够取得巨大的成功，一方面是因为GPT-3本身已经很强大了，它虽然输出的结果有些不尽如人意，但它是“有能力”输出好的回答的。只有在这样的基础上，我们再训练打分模型才有意义。另一方面，研究人员利用了强化学习的思路，将人工偏好注入了模型，使得经过调整的模型更知道如何给出人类想要的回答。

一些技术问题猜想

在实际使用当中，我们发现ChatGPT不仅仅是回答比以前更“智能”，还在其他方面出现了令人惊喜和意外的效果，由于原文中没有对这部分做详细阐述，以下是一些猜想：

ChatGPT的多轮对话能力

在传统的对话系统中，多轮对话中的省略，指代和话题一致性一直是比较难以解决的问题。但ChatGPT在这方面的表现非常令人惊讶。以下是几个可能的猜想：

1. 原始的数据当中就有对话数据，例如微调时，用到的数据里面有一部分是few-shot数据，这个里面就蕴含了对话信息
2. 模型的宽度达到了8072，远超一般多轮对话的总长度。所以只要在一次对话框内，每轮都将之前所有的问答信息+本轮提问输入到模型，就能实现类似多轮对话的效果

ChatGPT的交互修正能力

这也是ChatGPT表现出的超乎预料的一种能力，在对话过程中对之前的问题或者回答进行修正，ChatGPT都可以给出对应反馈。由于可以排除实时更新的可能，因为新开一轮对话，同样的错误ChatGPT还有可能会犯。因此源头可能还是在大规模语言模型的历史信息处理能力上。