【机器学习算法实践】AdaBoost是典型的Boosting算法，加法模型多个弱分类器流水线式的提升精度，更关注那些难处理的数据

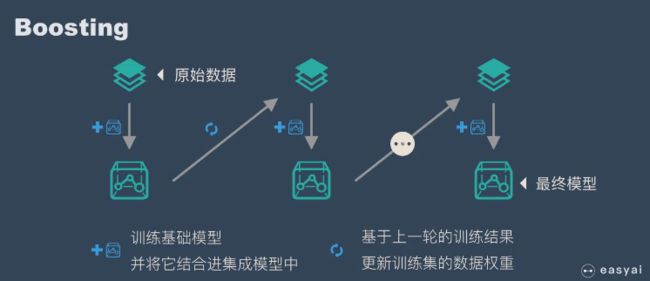
• 现实生活中，大家都知道“人多力量大”，“3 个臭皮匠顶个诸葛亮”。而集成学习的核心思路就是“人多力量大”，它并没有创造出新的算法，而是把已有的算法进行结合，从而得到更好的效果。集成学习会挑选一些简单的基础模型进行组装，组装这些基础模型的思路主要有 2 种方法：bagging（bootstrap aggregating的缩写，也称作“套袋法”）和boosting

• 

• Boosting 和 bagging 最本质的差别在于他对基础模型不是一致对待的，而是经过不停的考验和筛选来挑选出“精英”，然后给精英更多的投票权，表现不好的基础模型则给较少的投票权，然后综合所有人的投票得到最终结果。大部分情况下，经过 boosting 得到的结果偏差（bias）更小。一文看懂 Adaboost 算法 (与bagging算法对比 + 7 个优缺点） (easyai.tech)

  • 

• Boosting是一种集合技术，试图从许多弱分类器中创建一个强分类器。这是通过从训练数据构建模型，然后创建第二个模型来尝试从第一个模型中纠正错误来完成的。添加模型直到完美预测训练集或添加最大数量的模型。AdaBoost是第一个为二进制分类开发的真正成功的增强算法。这是理解助力的最佳起点。

• AdaBoost用于短决策树。在创建第一个树之后，每个训练实例上的树的性能用于加权创建的下一个树应该关注每个训练实例的注意力。难以预测的训练数据被赋予更多权重，而易于预测的实例被赋予更少的权重。模型一个接一个地顺序创建，每个模型更新训练实例上的权重，这些权重影响序列中下一个树所执行的学习。构建完所有树之后，将对新数据进行预测，并根据训练数据的准确性对每棵树的性能进行加权。因为通过算法如此关注纠正错误，所以必须删除带有异常值的干净数据。

• AdaBoost算法优缺点

  • 很好的利用了弱分类器进行级联；可以将不同的分类算法作为弱分类器；AdaBoost具有很高的精度；相对于bagging算法和Random Forest算法，AdaBoost充分考虑的每个分类器的权重。

  • AdaBoost迭代次数也就是弱分类器数目不太好设定，可以使用交叉验证来进行确定；数据不平衡导致分类精度下降；训练比较耗时，每次重新选择当前分类器最好切分点。AdaBoost对噪声数据和异常值敏感。

• AdaBoost，是英文"Adaptive Boosting"（自适应增强）的缩写，由Yoav Freund和Robert Schapire在1995年提出。它的自适应在于：前一个基本分类器分错的样本会得到加强，加权后的全体样本再次被用来训练下一个基本分类器（串行）。同时，在每一轮中加入一个新的弱分类器，直到达到某个预定的足够小的错误率或达到预先指定的最大迭代次数。

• 具体说来，整个Adaboost 迭代算法就3步：

• 初始化训练数据的权值分布。如果有N个样本，则每一个训练样本最开始时都被赋予相同的权值：1/N。

• 训练弱分类器。具体训练过程中，如果某个样本点已经被准确地分类，那么在构造下一个训练集中，它的权值就被降低；相反，如果某个样本点没有被准确地分类，那么它的权值就得到提高。然后，权值更新过的样本集被用于训练下一个分类器，整个训练过程如此迭代地进行下去。

• 将各个训练得到的弱分类器组合成强分类器。各个弱分类器的训练过程结束后，加大分类误差率小的弱分类器的权重，使其在最终的分类函数中起着较大的决定作用，而降低分类误差率大的弱分类器的权重，使其在最终的分类函数中起着较小的决定作用。换言之，误差率低的弱分类器在最终分类器中占的权重较大，否则较小。

• Adaboost算法流程

  • 给定一个训练数据集$T=(x_1,y_1),(x_2,y_2)\dots (x_N,y_N)$，其中实例 $x\in \mathcal{X}$，而实例空间 $\mathcal{X}\in {\mathbb{R}}^n$，yi属于标记集合{-1,+1}，Adaboost的目的就是从训练数据中学习一系列弱分类器或基本分类器，然后将这些弱分类器组合成一个强分类器。

  • 首先，初始化训练数据的权值分布。每一个训练样本最开始时都被赋予相同的权值：1/N。$D_1=(w_{11},w_{12},...,w_{1N}),w_{1i}=\frac{1}{N},i=1,2,...,N$。

  • 进行多轮迭代，用m = 1,2, …, M表示迭代的第多少轮：

    • 使用具有权值分布$D_m$的训练数据集学习，得到基本分类器（选取让误差率最低的阈值来设计基本分类器）：$G_n(x):\mathcal{X}\to \{-1,+1\}$；

    • 计算Gm(x)在训练数据集上的分类误差率：$e_m=P(G_m(x_i)\ne y_i)={\sum }_{i=1}^N{w}_{mi}I(G_m(x_i)\ne y_i)$,由式子可知，Gm(x)在训练数据集上的 误差率em就是被Gm(x)误分类样本的权值之和。

    • 计算Gm(x)的系数，$a_m$表示$G_m(x)$在最终分类器中的重要程度（目的：得到基本分类器在最终分类器中所占的权重。注：这个公式写成$a_m=\frac{1}{2}ln(\frac{(1-e_m)}{e_m})$更准确，因为底数是自然对数e，故用In，写成log容易让人误以为底数是2或别的底数）,由上述式子可知，$e_m<=\frac{1}{2}$时，$a_m>=0$，且$a_m$随着$e_m$的减小而增大，意味着分类误差率越小的基本分类器在最终分类器中的作用越大。

    • 更新训练数据集的权值分布（目的：得到样本的新的权值分布），用于下一轮迭代:$D_{m+1}=(w_{m+1,1},w_{m+1,2},...,w_{m+1,N}),w_{(m+1,i)}=\frac{w_{mi}}{Z_m}exp(-{\alpha }_m{y}_i{G}_m(x_i)),i=1,2,...,N$。使得被基本分类器Gm(x)误分类样本的权值增大，而被正确分类样本的权值减小。就这样，通过这样的方式，AdaBoost方法能“重点关注”或“聚焦于”那些较难分的样本上。 其中，$Zm$是规范化因子，使得$D_{m+1}$成为一个概率分布： $Z_m={\sum }_{i=1}^N{w}_{mi}exp(-{\alpha }_m{y}_i{G}_m(x_i))$。

  • 组合各个弱分类器 $f(x)={\sum }_{m=1}^M{\alpha }_m{G}_m(x)$。从而得到最终分类器，如下：$G(x)=sign(f(x))=sign({\sum }_{m=1}^M{\alpha }_m{G}_m(x)）$。

• Adaboost的误差界

• Adaboost在学习的过程中不断减少训练误差e，直到各个弱分类器组合成最终分类器，那这个最终分类器的误差界到底是多少呢？事实上，Adaboost 最终分类器的训练误差的上界为：$\frac{1}{N}{\sum }_{i=1}^{N}I(G(x_i)\ne y_i)\le \frac{1}{N}{\sum }_{i}exp(-y_{i}f(x_i))={\prod }_m{Z}_m$。

• 下面，咱们来通过推导来证明下上述式子。当$G(x_i)\ne y_i$时，$y_i\ast f(x_i)<0$，因而$exp(-y_i\ast f(x_i))\ge 1$，因此前半部分得证。关于后半部分，别忘了：$w_{m+1,i}=\frac{w_{mi}}{Z_m}exp(-{\alpha }_m{y}_i{G}_m(x_i))；Z_m{w}_{m+1,i}=w_{mi}exp(-{\alpha }_m{y}_i{G}_m(x_i))$。

• 整个的推导过程如下：

  $$\begin{array}{rl}\frac{1}{N}\sum _{i}exp(-y_{i}f(x_i))& \\ & =\frac{1}{N}\sum _{i}exp(-\sum _{m=1}^M{\alpha }_m{y}_i{G}_m(x_i))\\ & =w_{1i}\sum _{i}exp(-\sum _{m=1}^M{\alpha }_m{y}_i{G}_m(x_i))\\ & =w_{1i}\prod _{m=1}^{M}exp(-{\alpha }_m{y}_i{G}_m(x_i))\\ & =Z_1\sum _i{w}_{2i}\prod _{m=2}^{M}exp(-{\alpha }_m{y}_i{G}_m(x_i))\\ & =Z_1{Z}_2...Z_{M-1}\sum _i{w}_{mi}exp(-{\alpha }_m{y}_i{G}_m(x_i))\\ & =\prod _{m=1}^M{Z}_m\end{array}$$

• 这个结果说明，可以在每一轮选取适当的Gm使得Zm最小，从而使训练误差下降最快。接着，咱们来继续求上述结果的上界。 对于二分类而言，有如下结果：${\prod }_{m=1}^M{Z}_m={\prod }_{m=1}^M(2\sqrt{e_m(1-e_m)})={\prod }_{m=1}^M\sqrt{(1-4{\gamma }_m^2)}\le exp(-2{\sum }_{m=1}^M{\gamma }_m^2)$。其中${\gamma }_m=\frac{1}{2}-e_m$。

• 继续证明下这个结论。由之前$Z_m$的定义式跟本节最开始得到的结论可知：

  $$\begin{array}{rl}{Z}_m& =\sum _{i=1}^N{w}_{mi}exp(-{\alpha }_m{y}_i{G}_m(x_i))\\ & =\sum _{y_i=G_m(x_i)}{w}_{mi}exp(-{\alpha }_m)+\sum _{y_i\ne G_m(x_i)}{w}_{mi}exp({\alpha }_m)\\ & =(1-e_m)exp(-{\alpha }_m)+e_{m}exp({\alpha }_m)\\ & =2\sqrt{e_m(1-e_m)}\\ & =\sqrt{1-4{\gamma }_m^2}\end{array}$$

  而这个不等式${\prod }_{m=1}^M\sqrt{1-4{\gamma }_m^2}\le exp(-2{\sum }_{m=1}^M{\gamma }_m^2)$,可先由$e^x$和1-x的开根号，在点x的泰勒展开式推出。

  • 值得一提的是，如果取${\gamma }_1,{\gamma }_2\dots$ 的最小值，记做γ（显然，$\gamma \ge {\gamma }_i>0，i=1,2,...m$），则对于所有m，有： $\frac{1}{N}{\sum }_{i=1}^{N}I(G(x_i)\ne y_i)\le exp(-2M{\gamma }^2)$。

• 这个结论表明，AdaBoost的训练误差是以指数速率下降的。另外，AdaBoost算法不需要事先知道下界γ，AdaBoost具有自适应性，它能适应弱分类器各自的训练误差率 。

• AdaBoost是最著名的Boosting族算法。开始时，所有样本的权重相同，训练得到第一个基分类器。从第二轮开始，每轮开始前都先根据上一轮基分类器的分类效果调整每个样本的权重，上一轮分错的样本权重提高，分对的样本权重降低。之后根据新得到样本的权重指导本轮中的基分类器训练，即在考虑样本不同权重的情况下得到本轮错误率最低的基分类器。重复以上步骤直至训练到约定的轮数结束，每一轮训练得到一个基分类器。可以想象到，远离边界（超平面）的样本点总是分类正确，而分类边界附近的样本点总是有大概率被弱分类器（基分类器）分错，所以权值会变高，即边界附近的样本点会在分类时得到更多的重视。在训练过程中，每个新的模型都会基于前一个模型的表现结果进行调整，这也就是为什么AdaBoost是自适应（adaptive）的原因，即AdaBoost可以自动适应每个基学习器的准确率。

使用AdaBoost解决分类问题

• 导包，加载数据集，数据集：白酒数据，共有13个特征

  • import pandas as pd
    import numpy as np
    from sklearn.model_selection import train_test_split
    from sklearn.preprocessing import LabelEncoder # 使用LabelEncoder对数据集进行编码
    import matplotlib.pyplot as plt
    from sklearn.tree import DecisionTreeClassifier
    from sklearn.ensemble import AdaBoostClassifier
    from sklearn.metrics import accuracy_score
    data_dir = './data/'
    # Wine dataset and rank the 13 features by their respective importance measures
    df_wine = pd.read_csv(data_dir+'wine.data',
                          header=None,
                          names=['Class label', 'Alcohol', 'Malic acid', 'Ash', 'Alcalinity of ash', 'Magnesium',
                                   'Total phenols', 'Flavanoids', 'Nonflavanoid phenols', 'Proanthocyanins', 'Color intensity',
                                   'Hue', 'OD280/OD315 of diluted wines', 'Proline'])
    print('Class labels', np.unique(df_wine['Class label'])) # 一共有3个类
    df_wine = df_wine[df_wine['Class label']!=1] # 去掉一个类
    y = df_wine['Class label'].values
    X = df_wine[['Alcohol', 'OD280/OD315 of diluted wines']].values  # 提取两个特征属性
    print(len(X),len(y))
    

  • Class labels [1 2 3]
    119 119
    

• 数据预处理及划分,使用LabelEncoder对数据集进行编码

• from sklearn import preprocessing
  data=['小猫','小猫','小狗','小狗','兔子','兔子']  #准备好数据
  #方法1：
  enc=preprocessing.LabelEncoder()   #获取一个LabelEncoder
  enc=enc.fit(['小猫','小狗','兔子'])  #训练LabelEncoder
  data=enc.transform(data)       #使用训练好的LabelEncoder对原数据进行编码
  #方法2：
  #enc=preprocessing.LabelEncoder()   #获取一个LabelEncoder
  #data=enc.fit_transform(data) 
  print(data)    #输出编码后的数据
  # 根据编码后的类别，反向推导出编码前对应的原始标签 
  print(enc.inverse_transform([0,1,2]))
  

• [2 2 1 1 0 0] , [‘兔子’ ‘小狗’ ‘小猫’] # 根据结果可以看到， LabelEncoder将：小猫编码成2，小狗编码成2，兔子编码成0;根据输出结果可以看到，0对应兔子，1对应小狗，2对应小猫

  • le = LabelEncoder()  
    y = le.fit_transform(y)
    print('Class labels', np.unique(y))
    print('numbers of features:', X.shape[1])
    # 划分训练集测试集
    X_train, X_test, y_train, y_test = train_test_split(X, y, test_size=0.2, random_state=1, stratify=y)
    X_train.shape
    

  • Class labels [0 1]
    numbers of features: 2
    (95, 2)
    

• 先使用决策树做分类，作为GBDT的对比参照

  • tree = DecisionTreeClassifier(criterion='entropy', random_state=1, max_depth=1)
    tree = tree.fit(X_train, y_train)
    y_train_pred = tree.predict(X_train)
    y_test_pred = tree.predict(X_test)
    tree_train = accuracy_score(y_train, y_train_pred)
    tree_test = accuracy_score(y_test, y_test_pred)
    print('Decision tree train/test accuracies %.3f/%.3f' % (tree_train, tree_test))
    

  • Decision tree train/test accuracies 0.916/0.875
    

• 绘制决策边界adaboost

  • def plot_decision_regions(X, y, classifier_list, classifier_names):
        x_min = X[:, 0].min() - 1
        x_max = X[:, 0].max() + 1
        y_min = X[:, 1].min() - 1
        y_max = X[:, 1].max() + 1
        xx, yy = np.meshgrid(np.arange(x_min, x_max, 0.1),
        np.arange(y_min, y_max, 0.1))
        f, axarr = plt.subplots(1, 2, sharex='col', sharey='row', figsize=(8, 3))
        for idx, clf, tt in zip([0, 1],classifier_list,classifier_names):
            clf.fit(X, y)
            Z = clf.predict(np.c_[xx.ravel(), yy.ravel()])
            Z = Z.reshape(xx.shape)
            axarr[idx].contourf(xx, yy, Z, alpha=0.3)
            axarr[idx].scatter(X[y==0, 0], X[y==0, 1], c='blue', marker='^')
            axarr[idx].scatter(X[y==1, 0], X[y==1, 1], c='red', marker='o')
            axarr[idx].set_title(tt)
            axarr[0].set_ylabel('Alcohol', fontsize=12)
        plt.text(10.2, -0.5, s='OD280/OD315 of diluted wines', ha='center', va='center', fontsize=12)
        plt.show()
    ada = AdaBoostClassifier(estimator=tree,
                             n_estimators=500,
                             learning_rate=0.1,
                             random_state=1)
    ada = ada.fit(X_train, y_train)
    y_train_pred = ada.predict(X_train)
    y_test_pred = ada.predict(X_test)
    ada_train = accuracy_score(y_train, y_train_pred)
    ada_test = accuracy_score(y_test, y_test_pred)
    print('AdaBoost train/test accuracies %.3f/%.3f' % (ada_train, ada_test))
    plot_decision_regions(X_train, y_train, [tree, ada], ['Decision Tree', 'AdaBoost']) 
    

  • 

• 其实使用AdaBoost+DecisionTree分类树 基本就实现了GBDT分类问题

LightGBM实践

• GBDT (Gradient Boosting Decision Tree) 是机器学习中一个长盛不衰的模型，其主要思想是利用弱分类器（决策树）迭代训练以得到最优模型，该模型具有训练效果好、不易过拟合等优点。GBDT不仅在工业界应用广泛，通常被用于多分类、点击率预测、搜索排序等任务；在各种数据挖掘竞赛中也是致命武器，据统计Kaggle上的比赛有一半以上的冠军方案都是基于GBDT。而LightGBM（Light Gradient Boosting Machine）是一个实现GBDT算法的框架，支持高效率的并行训练，并且具有更快的训练速度、更低的内存消耗、更好的准确率、支持分布式可以快速处理海量数据等优点。

• 常用的机器学习算法，例如神经网络等算法，都可以以mini-batch的方式训练，训练数据的大小不会受到内存限制。而GBDT在每一次迭代的时候，都需要遍历整个训练数据多次。如果把整个训练数据装进内存则会限制训练数据的大小；如果不装进内存，反复地读写训练数据又会消耗非常大的时间。尤其面对工业级海量的数据，普通的GBDT算法是不能满足其需求的。LightGBM提出的主要原因就是为了解决GBDT在海量数据遇到的问题，让GBDT可以更好更快地用于工业实践。

• 数据说明：某城市各企业用电数据，从2015-1-1至2016-8-31，任务是预测未来一个月（即2016-9月）的用电情况，方法：特征工程+lightGBM Python-package Introduction — LightGBM 3.3.5.99 documentation

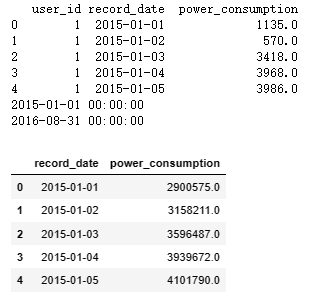
• import pandas as pd
  from matplotlib import pyplot as plt
  data_dir =  './data/'
  # 加载数据
  df = pd.read_csv(data_dir + 'tianchi_power_AI.csv')
  # 格式转换  将时间字符串转换为pandas认识的时间字段/列
  df['record_date'] = pd.to_datetime(df['record_date'])
  print(df.head())
  # 按每年每个月分组求和
  base_df = df[['record_date', 'power_consumption']].groupby(by='record_date').agg('sum')
  base_df = base_df.reset_index()
  print(base_df['record_date'].min())
  print(base_df['record_date'].max())
  base_df.head()
  

• 

• pd.to_datetime()解析来自各种来源和格式的时间序列信息pandas.to_datetime — pandas 1.5.3 documentation (pydata.org),pd.to_datetime(‘2023/3/24’, format=‘%Y/%m/%d’);pd.to_datetime(‘24-3-2023 00:00’, format=‘%d-%m-%Y %H:%M’)

• 特征工程,直接对每天的总量进行回归拟合，先提取用以回归的特征

  • df_test = base_df[ (base_df['record_date']>='2016-08-01') &
                       (base_df['record_date']<='2016-08-30')]
    # Timedelta： 时间差类型
    df_test['record_date'] = df_test['record_date']+pd.Timedelta('31 days') # 8月日期转9月日期
    print(df_test.head())
    base_df = pd.concat([base_df, df_test]).sort_values(['record_date']) # 包含了2016-9月预测月
    print(base_df.head())
    # 提取年、月、日、星期几、一月中的第几天、第几季度等特征
    base_df['dayofweek'] = base_df['record_date'].apply(lambda x: x.dayofweek)
    base_df['dayofyear'] = base_df['record_date'].apply(lambda x: x.dayofyear)
    base_df['day'] = base_df['record_date'].apply(lambda x: x.day)
    base_df['month'] = base_df['record_date'].apply(lambda x: x.month)
    base_df['year'] = base_df['record_date'].apply(lambda x: x.year)
    print(base_df.head())
    # 映射到第几季度
    def map_season(month):
        month_dict = {1:1, 2:1, 3:1, 4:2, 5:2, 6:2, 7:3, 8:3, 9:3, 10:4, 11:4, 12:4}
        return month_dict[month]
    base_df['season'] = base_df['month'].apply(lambda x: map_season(x))
    print(base_df.head())
    # 按每年每月分组 计算统计信息：均值、标准差
    base_df_stats = base_df[ ['power_consumption', 'year', 'month'] ].groupby(by=['year', 'month']).agg(['mean', 'std'])
    base_df_stats.columns = base_df_stats.columns.droplevel(0)
    print(base_df_stats.head())
    base_df_stats = base_df_stats.reset_index()
    print(base_df_stats.head())
    

  • 

  • base_df_stats['1_m_mean'] = base_df_stats['mean'].shift(1) # 向下移动1
    base_df_stats['2_m_mean'] = base_df_stats['mean'].shift(2) # 向下移动2
    base_df_stats['1_m_std'] = base_df_stats['std'].shift(1) # 向下移动1
    base_df_stats['2_m_std'] = base_df_stats['std'].shift(2) # 向下移动2
    print(base_df_stats.head())
    data_df = pd.merge(base_df, base_df_stats[ ['year', 'month', '1_m_mean', '2_m_mean', '1_m_std', '2_m_std'] ],
                       how='inner', on=['year', 'month'])
    print(data_df.head())
    data_df = data_df[~pd.isnull(data_df['2_m_mean'])] # 去掉Nan数据
    print(data_df.head())
    print(data_df.tail())
    

  • 

• lightGBM

  • %pip install lightgbm
    import lightgbm as lgb
    from sklearn.model_selection import GridSearchCV
    train_data = data_df[data_df['record_date']<'2016-09-01']\
        [['dayofweek','dayofyear','day','month','year','season','1_m_mean','2_m_mean','1_m_std','2_m_std']]
    test_data = data_df[data_df['record_date']>='2016-09-01']\
        [['dayofweek','dayofyear','day','month','year','season','1_m_mean','2_m_mean','1_m_std','2_m_std']]
    train_target = data_df[data_df['record_date']<'2016-09-01'][ ['power_consumption'] ]
    train_lgb = train_data.copy()
    # 日期/时间格式转换为str类型
    train_lgb[ ['dayofweek','dayofyear','day','month','year','season'] ] = \
        train_lgb[ ['dayofweek','dayofyear','day','month','year','season'] ].astype(str)
    test_lgb = test_data.copy()
    test_lgb[ ['dayofweek','dayofyear','day','month','year','season'] ] = \
        test_lgb[ ['dayofweek','dayofyear','day','month','year','season'] ].astype(str)
    X_lgb = train_lgb.values
    y_lgb = train_target.values.reshape(X_lgb.shape[0],)
    print(X_lgb.shape, y_lgb.shape, type(X_lgb))
    print(X_lgb[0, :])
    

  • (550, 10) (550,) <class 'numpy.ndarray'>
    ['6' '60' '1' '3' '2015' '1' 2795163.0535714286 3961383.0967741935
     769697.8649992085 303629.48662213905]
    

  • GridSearchCV的名字其实可以拆分为两部分，GridSearch和CV，即网格搜索和交叉验证。网格搜索，搜索的是参数，即在指定的参数范围内，按步长依次调整参数，利用调整的参数训练学习器，从所有的参数中找到在验证集上精度最高的参数，这其实是一个训练和比较的过程。k折交叉验证将所有数据集分成k份，不重复地每次取其中一份做测试集，用其余k-1份做训练集训练模型，之后计算该模型在测试集上的得分,将k次的得分取平均得到最后的得分。GridSearchCV可以保证在指定的参数范围内找到精度最高的参数，但是这也是网格搜索的缺陷所在，他要求遍历所有可能参数的组合，在面对大数据集和多参数的情况下，非常耗时。GridSearchCV，它存在的意义就是自动调参，只要把参数输进去，就能给出最优化结果和参数。但是这个方法适合于小数据集，一旦数据的量级上去了，很难得到结果。sklearn.model_selection.GridSearchCV — scikit-learn 1.2.2 documentation

  • 网格搜索可能是最简单，应用最广泛的超参数搜索算法，他通过查找搜索范围内的所有的点来确定最优值。如果采用较大的搜索范围及较小的步长，网格搜索很大概率找到全局最优值。然而这种搜索方案十分消耗计算资源和时间，特别是需要调优的超参数比较多的时候。因此在实际应用过程中，网格搜索法一般会先使用较广的搜索范围和较大的步长，来找到全局最优值可能的位置；然后再缩小搜索范围和步长，来寻找更精确的最优值。这种操作方案可以降低所需的时间和计算量，但由于目标函数一般是非凸的，所以很可能会错过全局最优值。

  • 模型参数,训练参数

  • # 模型参数
    estimator = lgb.LGBMRegressor(colsample_bytree=0.8, # 建每棵树时使用的属性列的比例（属性采样比例）
                                 subsample=0.9, # 使用训练样本的比例（样本采样比例）
                                 subsample_freq=5) # 采样频率
    param_grid = {
        'learning_rate': [0.01, 0.02, 0.05, 0.1],
        'n_estimators': [100, 200, 400, 800, 1000, 1200, 1500, 2000], # 要学习的boosted trees 个数
        'num_leaves': [128, 1024, 4096], # base learner的最大叶子节点数
    }
    # 训练参数
    fit_params = {'categorical_feature': [0,1,2,3,4,5]} # 哪些列是类别型特征，list of int则表示索引
    import warnings
    warnings.filterwarnings("ignore") # 不打印warning信息
    gbm = GridSearchCV(estimator, param_grid)
    gbm.fit(X_lgb, y_lgb, **fit_params)
    print('Best parameters found by grid search are:', gbm.best_params_)
    

  • Best parameters found by grid search are: {‘learning_rate’: 0.02, ‘n_estimators’: 1200, ‘num_leaves’: 128}

  • 使用最佳参数，重新训练模型

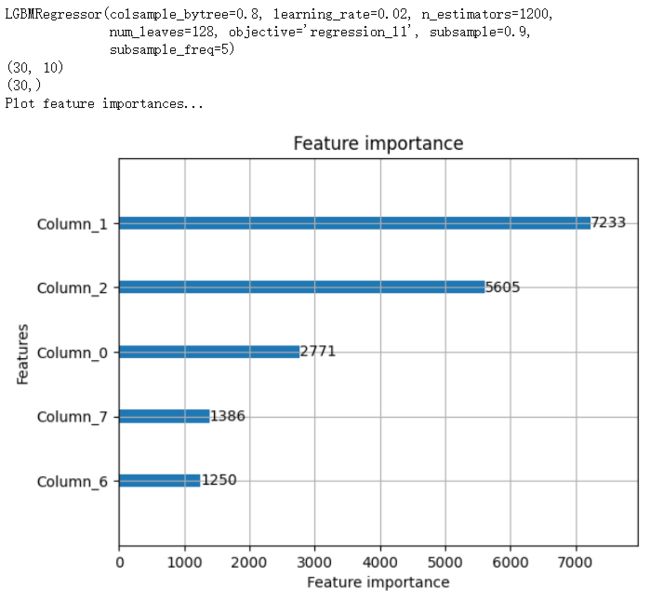
  • # 使用最佳参数，重新训练模型
    lgbm = lgb.LGBMRegressor(colsample_bytree=0.8, # 建每棵树时使用的属性列的比例（属性采样比例）
                             subsample=0.9, # 使用训练样本的比例（样本采样比例）
                             subsample_freq=5, # 采样频率
                             learning_rate=0.02,
                             n_estimators=1200,
                             num_leaves=128,
                             objective='regression_l1')
    print(lgbm.fit(X_lgb, y_lgb))
    X_pred = test_lgb.values
    print(X_pred.shape)
    y_pred = lgbm.predict(X_pred)
    print(y_pred.shape)
    print('Plot feature importances...')
    ax = lgb.plot_importance(lgbm, max_num_features=5) # max_num_features 显示最重要的5个特征
    plt.show()
    

  •