机器学习算法系列(十九)-自适应增强算法(Adaptive Boosting Algorithm / AdaBoost Algorithm)——下篇
接上篇
AdaBoost-SAMME 算法推导
同算法步骤中的前提条件一样,假设训练集 T = { X i , y i } T = \{ X_i, y_i \} T={Xi,yi}, i = 1 , . . . , N i = 1,...,N i=1,...,N,y 的取值有 M 种可能,h(x) 为估计器,估计器的数量为 K。
为了适应多分类问题,AdaBoost-SAMME 算法将原本为数值的标签 y 转化成一个向量的形式,如式 4-9 所示:
y ^ = { 1 y = m − 1 M − 1 y ≠ m m = 1 , … , M \hat{y} = \left\{ \begin{array}{c} 1 & y =m\\ -\frac{1}{M-1} & y \ne m \end{array}\right. \quad m = 1,\dots,M y^={1−M−11y=my=mm=1,…,M
下面用一个例子来说明式 4-9 的含义,假设标签 y 可取 1,2,3,标签集 y = { 2,1,2,3 },这时根据式 4-9 可以得到对应的转换后的标签集如式 4-10 所示:
y ∈ { 1 , 2 , 3 } y = { 2 , 1 , 2 , 3 } y ^ i = { 1 y i = m − 1 2 y i ≠ m m = 1 , 2 , 3 y ^ = [ − 1 2 1 − 1 2 1 − 1 2 − 1 2 − 1 2 1 − 1 2 − 1 2 − 1 2 1 ] \begin{array}{c} y \in \{1,2,3\} \\ y = \{2,1,2,3\} \\ \hat{y}_i = \left\{ \begin{array}{c} 1 & y_i =m\\ -\frac{1}{2} & y_i \ne m \end{array}\right. \quad m = 1,2,3 \\ \hat{y} = \begin{bmatrix} -\frac{1}{2} & 1 & -\frac{1}{2} \\ 1 & -\frac{1}{2} & -\frac{1}{2} \\ -\frac{1}{2} & 1 & -\frac{1}{2} \\ -\frac{1}{2} & -\frac{1}{2} & 1 \end{bmatrix} \end{array} y∈{1,2,3}y={2,1,2,3}y^i={1−21yi=myi=mm=1,2,3y^=⎣⎢⎢⎡−211−21−211−211−21−21−21−211⎦⎥⎥⎤
同样将算法解释为加法模型,通过多个估计器 h(x) 加权以后得到最后的强估计器 H(x),代价函数使用指数函数
(1)代价函数,这里比原始算法多了一个 1 M \frac{1}{M} M1,是为了后面计算方便,同时 H ( X i ) H(X_i) H(Xi)也是一个向量
(2)带入式 4-1 中的(3)式
(3)同样定义一个 ω,包含前一轮的强估计器等与 α 无关的值
(4)带入 ω 得到代价函数的表达式
(5)目标为找到最优的估计器权重 α 使得代价函数的取值最小
C o s t ( H ( x ) ) = ∑ i = 1 N e − 1 M y ^ i H ( X i ) ( 1 ) C o s t ( α ) = ∑ i = 1 N e − 1 M y ^ i ( H k − 1 ( X i ) + α h k ( X i ) ) ( 2 ) ω k , i ˉ = e − 1 M y ^ i H k − 1 ( X i ) ( 3 ) C o s t ( α ) = ∑ i = 1 N ω k , i ˉ e − 1 M y ^ i α h k ( X i ) ( 4 ) α k = argmin α ∑ i = 1 N ω k , i ˉ e − 1 M y ^ i α h k ( X i ) ( 5 ) \begin{aligned} Cost(H(x)) &= \sum_{i = 1}^{N} e^{-\frac{1}{M} \hat{y}_iH(X_i)} & (1) \\ Cost(\alpha) &= \sum_{i = 1}^{N} e^{-\frac{1}{M}\hat{y}_i(H_{k-1}(X_i) + \alpha h_k(X_i))} & (2) \\ \bar{\omega_{k,i}} &= e^{-\frac{1}{M}\hat{y}_iH_{k-1}(X_i)} & (3) \\ Cost(\alpha) &= \sum_{i = 1}^{N} \bar{\omega_{k,i}} e^{-\frac{1}{M}\hat{y}_i\alpha h_k(X_i)} & (4) \\ \alpha_k &= \underset{\alpha}{\operatorname{argmin} } \sum_{i = 1}^{N} \bar{\omega_{k,i}} e^{-\frac{1}{M}\hat{y}_i\alpha h_k(X_i)} & (5) \\ \end{aligned} Cost(H(x))Cost(α)ωk,iˉCost(α)αk=i=1∑Ne−M1y^iH(Xi)=i=1∑Ne−M1y^i(Hk−1(Xi)+αhk(Xi))=e−M1y^iHk−1(Xi)=i=1∑Nωk,iˉe−M1y^iαhk(Xi)=αargmini=1∑Nωk,iˉe−M1y^iαhk(Xi)(1)(2)(3)(4)(5)
我们先来看下代价函数中指数的部分,即预测值与标签值的点积,下面分两种情况讨论:
当预测值与标签值相同的时候,向量中 1 的位置一致, − 1 M − 1 -\frac{1}{M-1} −M−11 一共有 M - 1 个,得到如下的点积结果:
1 + ( M − 1 ) ( − 1 M − 1 ) ( − 1 M − 1 ) = M M − 1 \begin{aligned} 1 + \left(M - 1\right)\left(-\frac{1}{M-1}\right)\left(-\frac{1}{M-1}\right) = \frac{M}{M-1}\\ \end{aligned} 1+(M−1)(−M−11)(−M−11)=M−1M
当预测值与标签值不相同的时候,向量中 1 的位置不一致, − 1 M − 1 -\frac{1}{M-1} −M−11 一共有 M - 2 个,得到如下的点积结果:
( − 1 M − 1 ) + ( − 1 M − 1 ) + ( M − 2 ) ( − 1 M − 1 ) ( − 1 M − 1 ) = − M ( M − 1 ) 2 \begin{aligned} \left(-\frac{1}{M-1}\right) + \left(-\frac{1}{M-1}\right) + \left(M - 2\right) \left(-\frac{1}{M-1}\right)\left(-\frac{1}{M-1}\right) = -\frac{M}{(M-1)^2} \end{aligned} (−M−11)+(−M−11)+(M−2)(−M−11)(−M−11)=−(M−1)2M
综合上面两种情况,得到如下的结果:
y ^ i h k ( X i ) = { M M − 1 y ^ i = h k ( X i ) − M ( M − 1 ) 2 y ^ i ≠ h k ( X i ) \hat{y}_ih_k(X_i) = \left\{ \begin{aligned} &\frac{M}{M-1} & \hat{y}_i = h_k(X_i) \\ &-\frac{M}{(M-1)^2} & \hat{y}_i \ne h_k(X_i) \end{aligned} \right. y^ihk(Xi)=⎩⎪⎪⎨⎪⎪⎧M−1M−(M−1)2My^i=hk(Xi)y^i=hk(Xi)
(1)代价函数 C o s t ( α ) Cost(α) Cost(α)
(2)分两种情况带入式 4-14
(3)增加第二、三两项,不影响最后的结果
(4)将(3)式中前两项和后两项分别合并得到
C o s t ( α ) = ∑ i = 1 N ω k , i ˉ e − 1 M y ^ i α h k ( X i ) ( 1 ) = ∑ y ^ i = h k ( X i ) N ω k , i ˉ e − α M − 1 + ∑ y ^ i ≠ h k ( X i ) N ω k , i ˉ e α ( M − 1 ) 2 ( 2 ) = ∑ y ^ i = h k ( X i ) N ω k , i ˉ e − α M − 1 + ∑ y ^ i ≠ h k ( X i ) N ω k , i ˉ e − α M − 1 − ∑ y ^ i ≠ h k ( X i ) N ω k , i ˉ e − α M − 1 + ∑ y ^ i ≠ h k ( X i ) N ω k , i ˉ e α ( M − 1 ) 2 ( 3 ) = e − α M − 1 ∑ i = 1 N ω k , i ˉ + ( e α ( M − 1 ) 2 − e − α M − 1 ) ∑ i = 1 N ω k , i ˉ I ( y ^ i ≠ h k ( X i ) ) ( 4 ) \begin{aligned} Cost(\alpha) &= \sum_{i = 1}^{N} \bar{\omega_{k,i}} e^{-\frac{1}{M}\hat{y}_i\alpha h_k(X_i)} & (1) \\ &= \sum_{\hat{y}_i = h_k(X_i)}^{N} \bar{\omega_{k,i}} e^{-\frac{\alpha}{M-1} } + \sum_{\hat{y}_i \ne h_k(X_i)}^{N} \bar{\omega_{k,i}} e^{\frac{\alpha}{(M-1)^2}} & (2) \\ &= \sum_{\hat{y}_i = h_k(X_i)}^{N} \bar{\omega_{k,i}} e^{-\frac{\alpha}{M-1} } + \sum_{\hat{y}_i \ne h_k(X_i)}^{N} \bar{\omega_{k,i}} e^{-\frac{\alpha}{M-1}} - \sum_{\hat{y}_i \ne h_k(X_i)}^{N} \bar{\omega_{k,i}} e^{-\frac{\alpha}{M-1}} + \sum_{\hat{y}_i \ne h_k(X_i)}^{N} \bar{\omega_{k,i}} e^{\frac{\alpha}{(M-1)^2}} & (3) \\ &= e^{-\frac{\alpha}{M-1} } \sum_{i = 1}^{N} \bar{\omega_{k,i}} + (e^{\frac{\alpha}{(M-1)^2}} - e^{-\frac{\alpha}{M-1}}) \sum_{i = 1}^{N} \bar{\omega_{k,i}} I(\hat{y}_i \ne h_k(X_i)) & (4) \\ \end{aligned} Cost(α)=i=1∑Nωk,iˉe−M1y^iαhk(Xi)=y^i=hk(Xi)∑Nωk,iˉe−M−1α+y^i=hk(Xi)∑Nωk,iˉe(M−1)2α=y^i=hk(Xi)∑Nωk,iˉe−M−1α+y^i=hk(Xi)∑Nωk,iˉe−M−1α−y^i=hk(Xi)∑Nωk,iˉe−M−1α+y^i=hk(Xi)∑Nωk,iˉe(M−1)2α=e−M−1αi=1∑Nωk,iˉ+(e(M−1)2α−e−M−1α)i=1∑Nωk,iˉI(y^i=hk(Xi))(1)(2)(3)(4)
(1)对代价函数求导数并令其为零
(2)定义错误率 e k e_k ek 的表达式
(3)将错误率 e k e_k ek 带入(2)式
(4)两边同时乘以 e α M − 1 e^{\frac{\alpha}{M-1}} eM−1α
(5)移项后整理得
(6)求得最后的估计器权重 α 的表达式
∂ C o s t ( α ) ∂ α = ( − 1 M − 1 ) e − α M − 1 ∑ i = 1 N ω k , i ˉ + ( ( 1 ( M − 1 ) 2 ) e α ( M − 1 ) 2 + ( 1 ( M − 1 ) ) e − α M − 1 ) ∑ i = 1 N ω k , i ˉ I ( y i ≠ h k ( X i ) ) = 0 ( 1 ) e k = ∑ i = 1 N ω k , i ˉ I ( y i ≠ h k ( X i ) ) ∑ i = 1 N ω k , i ˉ ( 2 ) e − α M − 1 = ( ( 1 M − 1 ) e α ( M − 1 ) 2 + e − α M − 1 ) e k ( 3 ) 1 = ( ( 1 M − 1 ) e α ( M − 1 ) 2 + α M − 1 + 1 ) e k ( 4 ) 1 − e k e k = ( 1 M − 1 ) e M α ( M − 1 ) 2 ( 5 ) α = ( M − 1 ) 2 M ( ln ( 1 − e k e k ) + ln ( M − 1 ) ) ( 6 ) \begin{aligned} \frac{\partial Cost(\alpha )}{\partial \alpha } &= \left(-\frac{1}{M-1}\right)e^{-\frac{\alpha}{M-1}} \sum_{i = 1}^{N} \bar{\omega_{k,i}} + \left(\left(\frac{1}{(M-1)^2}\right)e^{\frac{\alpha}{(M-1)^2}} + \left(\frac{1}{(M-1)}\right)e^{-\frac{\alpha}{M-1}}\right) \sum_{i = 1}^{N} \bar{\omega_{k,i}} I(y_i \ne h_k(X_i)) = 0& (1) \\ e_k &= \frac{\sum_{i = 1}^{N}\bar{\omega_{k,i}} I(y_i \ne h_k(X_i))}{\sum_{i = 1}^{N}\bar{\omega_{k,i}}} & (2) \\ e^{-\frac{\alpha}{M-1}} &= \left(\left(\frac{1}{M-1}\right)e^{\frac{\alpha}{(M-1)^2}} + e^{-\frac{\alpha}{M-1}}\right) e_k & (3) \\ 1 &= \left(\left(\frac{1}{M-1}\right)e^{\frac{\alpha}{(M-1)^2} + \frac{\alpha}{M-1}} + 1\right) e_k & (4) \\ \frac{1 - e_k}{e_k} &= \left(\frac{1}{M-1}\right)e^{\frac{M\alpha}{(M-1)^2}} & (5) \\ \alpha &= \frac{(M-1)^2}{M}\left( \ln \left(\frac{1 - e_k}{e_k}\right) + \ln (M - 1) \right) & (6) \end{aligned} ∂α∂Cost(α)eke−M−1α1ek1−ekα=(−M−11)e−M−1αi=1∑Nωk,iˉ+(((M−1)21)e(M−1)2α+((M−1)1)e−M−1α)i=1∑Nωk,iˉI(yi=hk(Xi))=0=∑i=1Nωk,iˉ∑i=1Nωk,iˉI(yi=hk(Xi))=((M−11)e(M−1)2α+e−M−1α)ek=((M−11)e(M−1)2α+M−1α+1)ek=(M−11)e(M−1)2Mα=M(M−1)2(ln(ek1−ek)+ln(M−1))(1)(2)(3)(4)(5)(6)
式 4-16 中估计器权重 α 的表达式前面的常数在进过归一化后对结果没有影响,后面的样本权重更新的公式一样也是简化后的结果。更多详细的算法说明请参考原始论文——Multi-class AdaBoost7
AdaBoost-SAMME.R 算法推导
AdaBoost-SAMME.R 算法是 AdaBoost-SAMME 算法的变体,该算法是使用加权概率估计来更新加法模型,如式 4-17 所示:
H k ( x ) = H k − 1 ( x ) + h k ( x ) \begin{aligned} H_k(x) = H_{k - 1}(x) + h_k(x) \end{aligned} Hk(x)=Hk−1(x)+hk(x)
代价函数使用的依然是指数函数,不同的是已经没有了估计器权重或者说每一个估计器的权重都为 1,且改成了期望的形式,其中 h(x) 返回的是 M 维的向量,同时为保证求出的 h(x) 唯一,加上了向量的各个元素之和为 0 的限制条件。
h k ( x ) = argmax h ( x ) E ( e − 1 M y ^ i ( H k − 1 ( x ) + h ( x ) ) ∣ x ) s . t . h k 1 ( x ) + h k 2 ( x ) + ⋯ + h k M ( x ) = 0 \begin{array}{c} h_k(x) = \underset{h(x)}{\operatorname{argmax}} E(e^{-\frac{1}{M} \hat{y}_i (H_{k-1}(x) + h(x)) } \mid x) \\ s.t. \quad h_k^1(x) + h_k^2(x) + \cdots + h_k^M(x) = 0 \end{array} hk(x)=h(x)argmaxE(e−M1y^i(Hk−1(x)+h(x))∣x)s.t.hk1(x)+hk2(x)+⋯+hkM(x)=0
代价函数可以拆分成对每一类分别求期望后再相加:
C o s t ( h ( x ) ) = E ( e − 1 M y ^ i ( H k − 1 ( x ) + h ( x ) ) ∣ x ) ( 1 ) = E ( e − 1 M y ^ i H k − 1 ( x ) e − 1 M y ^ i h ( x ) ∣ x ) ( 2 ) = E ( e − 1 M y ^ i H k − 1 ( x ) e − 1 M y ^ i h ( x ) I ( y = 1 ) ∣ x ) + ⋯ + E ( e − 1 M y ^ i H k − 1 ( x ) e − 1 M y ^ i h ( x ) I ( y = M ) ∣ x ) ( 3 ) \begin{aligned} Cost(h(x)) &= E(e^{-\frac{1}{M} \hat{y}_i (H_{k-1}(x) + h(x)) } \mid x) & (1) \\ &= E(e^{-\frac{1}{M} \hat{y}_i H_{k-1}(x)}e^{-\frac{1}{M}\hat{y}_ih(x) } \mid x) & (2) \\ &= E(e^{-\frac{1}{M} \hat{y}_i H_{k-1}(x)}e^{-\frac{1}{M}\hat{y}_ih(x) } I(y = 1) \mid x) + \cdots + E(e^{-\frac{1}{M} \hat{y}_i H_{k-1}(x)}e^{-\frac{1}{M}\hat{y}_ih(x) } I(y = M) \mid x) & (3) \\ \end{aligned} Cost(h(x))=E(e−M1y^i(Hk−1(x)+h(x))∣x)=E(e−M1y^iHk−1(x)e−M1y^ih(x)∣x)=E(e−M1y^iHk−1(x)e−M1y^ih(x)I(y=1)∣x)+⋯+E(e−M1y^iHk−1(x)e−M1y^ih(x)I(y=M)∣x)(1)(2)(3)
先来看看当 y = 1 时,y * h(x) 的结果:
(1)当 y = 1 时,转换后 y 的向量形式
(2)计算点积的结果
(3)合并最后的项
(4)根据限制条件替换
(5)得到化简后的结果
y ^ = [ 1 , − 1 M − 1 , ⋯ , − 1 M − 1 ] ( 1 ) y ^ i h ( x ) = h 1 ( x ) + ( − 1 M − 1 ) h 2 ( x ) + ⋯ + ( − 1 M − 1 ) h M ( x ) ( 2 ) = h 1 ( x ) − h 2 ( x ) + ⋯ + h M ( x ) M − 1 ( 3 ) = h 1 ( x ) − − h 1 ( x ) M − 1 ( 4 ) = M h 1 ( x ) M − 1 ( 5 ) \begin{aligned} \hat{y} &= [1, -\frac{1}{M - 1}, \cdots, -\frac{1}{M - 1} ] & (1) \\ \hat{y}_ih(x) &= h^1(x) + (-\frac{1}{M - 1})h^2(x) + \cdots + (-\frac{1}{M - 1})h^M(x) & (2) \\ &= h^1(x) - \frac{h^2(x) + \cdots + h^M(x)}{M - 1} & (3) \\ &= h^1(x) - \frac{-h^1(x)}{M - 1} & (4) \\ &= \frac{Mh^1(x)}{M - 1} & (5) \\ \end{aligned} y^y^ih(x)=[1,−M−11,⋯,−M−11]=h1(x)+(−M−11)h2(x)+⋯+(−M−11)hM(x)=h1(x)−M−1h2(x)+⋯+hM(x)=h1(x)−M−1−h1(x)=M−1Mh1(x)(1)(2)(3)(4)(5)
(1)带入式 4-20
(2)提出与期望无关的项
(3)另后面的期望为 P ( y = 1 ∣ x ) P(y = 1 | x) P(y=1∣x)
(4)同理可以得每一类的期望结果
E ( e − 1 M y ^ i H k − 1 ( x ) e − 1 M y ^ i h ( x ) I ( y = 1 ) ∣ x ) = E ( e − 1 M y ^ i H k − 1 ( x ) e − h 1 ( x ) M − 1 I ( y = 1 ) ∣ x ) ( 1 ) = e − h 1 ( x ) M − 1 E ( e − 1 M y ^ i H k − 1 ( x ) I ( y = 1 ) ∣ x ) ( 2 ) P ( y = 1 ∣ x ) = E ( e − 1 M y ^ i H k − 1 ( x ) I ( y = 1 ) ∣ x ) ( 3 ) E ( e − 1 M y ^ i H k − 1 ( x ) e − 1 M y ^ i h ( x ) I ( y = m ) ∣ x ) = e − h m ( x ) M − 1 P ( y = m ∣ x ) ( 4 ) \begin{aligned} E(e^{-\frac{1}{M} \hat{y}_i H_{k-1}(x)}e^{-\frac{1}{M}\hat{y}_ih(x) } I(y = 1) \mid x) &= E(e^{-\frac{1}{M} \hat{y}_i H_{k-1}(x)}e^{-\frac{h^1(x)}{M-1} } I(y = 1) \mid x) & (1) \\ &= e^{-\frac{h^1(x)}{M-1}} E(e^{-\frac{1}{M} \hat{y}_i H_{k-1}(x)} I(y = 1) \mid x) & (2) \\ P(y = 1 | x) &= E(e^{-\frac{1}{M} \hat{y}_i H_{k-1}(x)} I(y = 1) \mid x) & (3) \\ E(e^{-\frac{1}{M} \hat{y}_i H_{k-1}(x)}e^{-\frac{1}{M}\hat{y}_ih(x) } I(y = m) \mid x) &= e^{-\frac{h^m(x)}{M-1}} P(y = m | x) & (4) \\ \end{aligned} E(e−M1y^iHk−1(x)e−M1y^ih(x)I(y=1)∣x)P(y=1∣x)E(e−M1y^iHk−1(x)e−M1y^ih(x)I(y=m)∣x)=E(e−M1y^iHk−1(x)e−M−1h1(x)I(y=1)∣x)=e−M−1h1(x)E(e−M1y^iHk−1(x)I(y=1)∣x)=E(e−M1y^iHk−1(x)I(y=1)∣x)=e−M−1hm(x)P(y=m∣x)(1)(2)(3)(4)
将上面的结果带入代价函数得:
C o s t ( h ( x ) ) = e − h 1 ( x ) M − 1 P ( y = 1 ∣ x ) + ⋯ + e − h M ( x ) M − 1 P ( y = M ∣ x ) ( 1 ) = ∑ m = 1 M e − h m ( x ) M − 1 P ( y = m ∣ x ) ( 2 ) \begin{aligned} Cost(h(x)) &= e^{-\frac{h^1(x)}{M-1}} P(y = 1 | x) + \cdots + e^{-\frac{h^M(x)}{M-1}} P(y = M | x) & (1) \\ &= \sum_{m = 1}^{M} e^{-\frac{h^m(x)}{M-1}} P(y = m | x) & (2) \\ \end{aligned} Cost(h(x))=e−M−1h1(x)P(y=1∣x)+⋯+e−M−1hM(x)P(y=M∣x)=m=1∑Me−M−1hm(x)P(y=m∣x)(1)(2)
这时可以使用拉格朗日乘数法来求解上述问题,其拉格朗日函数 L 如下:
L ( h ( x ) , λ ) = ∑ m = 1 M e − h m ( x ) M − 1 P ( y = m ∣ x ) − λ ∑ m = 1 M h m ( x ) \begin{aligned} L(h(x), \lambda ) &= \sum_{m = 1}^{M} e^{-\frac{h^m(x)}{M-1}} P(y = m | x) - \lambda \sum_{m = 1}^{M} h^m(x)\\ \end{aligned} L(h(x),λ)=m=1∑Me−M−1hm(x)P(y=m∣x)−λm=1∑Mhm(x)
拉格朗日函数分别对 h(x) 的各个分量求导数:
∂ L ( h ( x ) , λ ) ∂ h 1 ( x ) = − 1 M − 1 e − h 1 ( x ) M − 1 P ( y = 1 ∣ x ) − λ = 0 ∂ L ( h ( x ) , λ ) ∂ h 2 ( x ) = − 1 M − 1 e − h 2 ( x ) M − 1 P ( y = 2 ∣ x ) − λ = 0 ⋯ ∂ L ( h ( x ) , λ ) ∂ h M ( x ) = − 1 M − 1 e − h M ( x ) M − 1 P ( y = M ∣ x ) − λ = 0 \begin{aligned} \frac{\partial L(h(x), \lambda)}{\partial h^1(x)} &= -\frac{1}{M-1} e^{-\frac{h^1(x)}{M-1}} P(y = 1 | x) - \lambda = 0 \\ \frac{\partial L(h(x), \lambda)}{\partial h^2(x)} &= -\frac{1}{M-1} e^{-\frac{h^2(x)}{M-1}} P(y = 2 | x) - \lambda = 0 \\ & \cdots \\ \frac{\partial L(h(x), \lambda)}{\partial h^M(x)} &= -\frac{1}{M-1} e^{-\frac{h^M(x)}{M-1}} P(y = M | x) - \lambda = 0 \\ \end{aligned} ∂h1(x)∂L(h(x),λ)∂h2(x)∂L(h(x),λ)∂hM(x)∂L(h(x),λ)=−M−11e−M−1h1(x)P(y=1∣x)−λ=0=−M−11e−M−1h2(x)P(y=2∣x)−λ=0⋯=−M−11e−M−1hM(x)P(y=M∣x)−λ=0
两两联立式 4-24 ,分别求出各个分量的结果,下面以第一个为例:
(1)联立导数中的第 1,2 式子
(2)消掉相同的常数项再两边同时取对数
(3)移项化简后得
− 1 M − 1 e − h 1 ( x ) M − 1 P ( y = 1 ∣ x ) = − 1 M − 1 e − h 2 ( x ) M − 1 P ( y = 2 ∣ x ) ( 1 ) − h 1 ( x ) M − 1 + ln P ( y = 1 ∣ x ) = − h 2 ( x ) M − 1 + ln P ( y = 2 ∣ x ) ( 2 ) h 1 ( x ) − h 2 ( x ) = ( M − 1 ) ( ln P ( y = 1 ∣ x ) − ln P ( y = 2 ∣ x ) ) ( 3 ) \begin{aligned} -\frac{1}{M-1} e^{-\frac{h^1(x)}{M-1}} P(y = 1 | x) &= -\frac{1}{M-1} e^{-\frac{h^2(x)}{M-1}} P(y = 2 | x) & (1)\\ -\frac{h^1(x)}{M-1} + \ln P(y = 1 | x) &= -\frac{h^2(x)}{M-1} + \ln P(y = 2 | x) & (2) \\ h^1(x) - h^2(x) &= (M - 1) (\ln P(y = 1 | x) - \ln P(y = 2 | x)) & (3) \\ \end{aligned} −M−11e−M−1h1(x)P(y=1∣x)−M−1h1(x)+lnP(y=1∣x)h1(x)−h2(x)=−M−11e−M−1h2(x)P(y=2∣x)=−M−1h2(x)+lnP(y=2∣x)=(M−1)(lnP(y=1∣x)−lnP(y=2∣x))(1)(2)(3)
(1)~(3)同理可得
(4)将(1)~(3)式累加起来根据限制条件化简
(5)将最后一项补充完整
(6)得到第一个分量的结果
h 1 ( x ) − h 2 ( x ) = ( M − 1 ) ( ln P ( y = 1 ∣ x ) − ln P ( y = 2 ∣ x ) ) ( 1 ) h 1 ( x ) − h 3 ( x ) = ( M − 1 ) ( ln P ( y = 1 ∣ x ) − ln P ( y = 3 ∣ x ) ) ( 2 ) ⋯ h 1 ( x ) − h M ( x ) = ( M − 1 ) ( ln P ( y = 1 ∣ x ) − ln P ( y = M ∣ x ) ) ( 3 ) ( M − 1 ) h 1 ( x ) − ( − h 1 ( x ) ) = ( M − 1 ) ( ( M − 1 ) ln P ( y = 1 ∣ x ) − ∑ m ≠ 1 ln P ( y = m ∣ x ) ) ) ( 4 ) M h 1 ( x ) = ( M − 1 ) ( M ln P ( y = 1 ∣ x ) − ∑ m = 1 M ln P ( y = m ∣ x ) ) ( 5 ) h 1 ( x ) = ( M − 1 ) ( ln P ( y = 1 ∣ x ) − 1 M ∑ m = 1 M ln P ( y = m ∣ x ) ) ( 6 ) \begin{aligned} h^1(x) - h^2(x) &= (M - 1) (\ln P(y = 1 | x) - \ln P(y = 2 | x)) & (1) \\ h^1(x) - h^3(x) &= (M - 1) (\ln P(y = 1 | x) - \ln P(y = 3 | x)) & (2) \\ & \cdots \\ h^1(x) - h^M(x) &= (M - 1) (\ln P(y = 1 | x) - \ln P(y = M | x)) & (3) \\ (M - 1) h^1(x) - (-h^1(x)) &= (M - 1)((M - 1)\ln P(y = 1 | x) - \sum_{m \ne 1} \ln P(y = m | x))) & (4) \\ Mh^1(x) &= (M - 1)(M\ln P(y = 1 | x) - \sum_{m = 1}^{M} \ln P(y = m | x)) & (5) \\ h^1(x) &= (M - 1)(\ln P(y = 1 | x) - \frac{1}{M} \sum_{m = 1}^{M} \ln P(y = m | x)) & (6) \\ \end{aligned} h1(x)−h2(x)h1(x)−h3(x)h1(x)−hM(x)(M−1)h1(x)−(−h1(x))Mh1(x)h1(x)=(M−1)(lnP(y=1∣x)−lnP(y=2∣x))=(M−1)(lnP(y=1∣x)−lnP(y=3∣x))⋯=(M−1)(lnP(y=1∣x)−lnP(y=M∣x))=(M−1)((M−1)lnP(y=1∣x)−m=1∑lnP(y=m∣x)))=(M−1)(MlnP(y=1∣x)−m=1∑MlnP(y=m∣x))=(M−1)(lnP(y=1∣x)−M1m=1∑MlnP(y=m∣x))(1)(2)(3)(4)(5)(6)
同理可得 h(x) 各个分量的结果
h m ( x ) = ( M − 1 ) ( ln P ( y = m ∣ x ) − 1 M ∑ m ′ = 1 M ln P ( y = m ′ ∣ x ) ) \begin{aligned} h^m(x) &= (M - 1)(\ln P(y = m | x) - \frac{1}{M} \sum_{m^{'} = 1}^{M} \ln P(y = m^{'} | x)) \\ \end{aligned} hm(x)=(M−1)(lnP(y=m∣x)−M1m′=1∑MlnP(y=m′∣x))
样本权重的更新如下,将 h(x) 带入更新方法中,可以看到更新方法只保留了前面一项,因为后面一项为每一类的 p(x) 求和,可以认为是一个常数,归一化以后不影响最后的结果。
ω k , i ˉ = e − 1 M y ^ i H k − 1 ( X i ) ( 1 ) ω k + 1 , i ˉ = ω k , i ˉ e − 1 M y ^ i h k ( X i ) ( 2 ) = ω k , i ˉ e − M − 1 M y ^ i ln p k ( X i ) ( 3 ) \begin{aligned} \bar{\omega_{k,i}} &= e^{-\frac{1}{M}\hat{y}_iH_{k-1}(X_i)} & (1) \\ \bar{\omega_{k+1,i}} &= \bar{\omega_{k,i}} e^{-\frac{1}{M}\hat{y}_ih_{k}(X_i)} & (2) \\ &= \bar{\omega_{k,i}} e^{-\frac{M - 1}{M}\hat{y}_i\ln p_k(X_i)} & (3) \\ \end{aligned} ωk,iˉωk+1,iˉ=e−M1y^iHk−1(Xi)=ωk,iˉe−M1y^ihk(Xi)=ωk,iˉe−MM−1y^ilnpk(Xi)(1)(2)(3)
这样就得到了算法步骤中的样本权重的更新公式,更多详细的算法说明也请参考原始论文——Multi-class AdaBoost7
五、代码实现
使用 Python 实现 AdaBoost 算法
import numpy as np
from sklearn.tree import DecisionTreeClassifier
class adaboostc():
"""
AdaBoost 分类算法
"""
def __init__(self, n_estimators = 100):
# AdaBoost弱学习器数量
self.n_estimators = n_estimators
def fit(self, X, y):
"""
AdaBoost 分类算法拟合
"""
# 初始化样本权重向量
sample_weights = np.ones(X.shape[0]) / X.shape[0]
# 估计器数组
estimators = []
# 估计器权重数组
weights = []
# 遍历估计器
for i in range(self.n_estimators):
# 初始化最大深度为1的决策树估计器
estimator = DecisionTreeClassifier(max_depth = 1)
# 按照样本权重拟合训练集
estimator.fit(X, y, sample_weight=sample_weights)
# 预测训练集
y_predict = estimator.predict(X)
# 计算误差率
e = np.sum(sample_weights[y_predict != y])
# 当误差率大于等于0.5时跳出循环
if e >= 0.5:
self.n_estimators = i
break
# 计算估计器权重
weight = 0.5 * np.log((1 - e) / e)
# 计算样本权重
temp_weights = np.multiply(sample_weights, np.exp(- weight * np.multiply(y, y_predict)))
# 归一化样本权重
sample_weights = temp_weights / np.sum(temp_weights)
weights.append(weight)
estimators.append(estimator)
self.weights = weights
self.estimators = estimators
def predict(self, X):
"""
AdaBoost 分类算法预测
"""
y = np.zeros(X.shape[0])
# 遍历估计器
for i in range(self.n_estimators):
estimator = self.estimators[i]
weight = self.weights[i]
# 预测结果
predicts = estimator.predict(X)
# 按照估计器的权重累加
y += weight * predicts
# 根据权重的正负号返回结果
return np.sign(y)
使用 Python 实现 AdaBoost-SAMME 算法
import numpy as np
from sklearn.tree import DecisionTreeClassifier
class adaboostmc():
"""
AdaBoost 多分类SAMME算法
"""
def __init__(self, n_estimators = 100):
# AdaBoost弱学习器数量
self.n_estimators = n_estimators
def fit(self, X, y):
"""
AdaBoost 多分类SAMME算法拟合
"""
# 标签分类
self.classes = np.unique(y)
# 标签分类数
self.n_classes = len(self.classes)
# 初始化样本权重向量
sample_weights = np.ones(X.shape[0]) / X.shape[0]
# 估计器数组
estimators = []
# 估计器权重数组
weights = []
# 遍历估计器
for i in range(self.n_estimators):
# 初始化最大深度为1的决策树估计器
estimator = DecisionTreeClassifier(max_depth = 1)
# 按照样本权重拟合训练集
estimator.fit(X, y, sample_weight=sample_weights)
# 训练集预测结果
y_predict = estimator.predict(X)
incorrect = y_predict != y
# 计算误差率
e = np.sum(sample_weights[incorrect])
# 计算估计器权重
weight = np.log((1 - e) / e) + np.log(self.n_classes - 1)
# 计算样本权重
temp_weights = np.multiply(sample_weights, np.exp(weight * incorrect))
# 归一化样本权重
sample_weights = temp_weights / np.sum(temp_weights)
weights.append(weight)
estimators.append(estimator)
self.weights = weights
self.estimators = estimators
def predict(self, X):
"""
AdaBoost 多分类SAMME算法预测
"""
# 加权结果集合
results = np.zeros((X.shape[0], self.n_classes))
# 遍历估计器
for i in range(self.n_estimators):
estimator = self.estimators[i]
weight = self.weights[i]
# 预测结果
predicts = estimator.predict(X)
# 遍历标签分类
for j in range(self.n_classes):
# 对应标签分类的权重累加
results[predicts == self.classes[j], j] += weight
# 取加权最大对应的分类作为最后的结果
return self.classes.take(np.argmax(results, axis=1), axis=0)
使用 Python 实现 AdaBoost-SAMME.R 算法
import numpy as np
from sklearn.tree import DecisionTreeClassifier
class adaboostmcr():
"""
AdaBoost 多分类SAMME.R算法
"""
def __init__(self, n_estimators = 100):
# AdaBoost弱学习器数量
self.n_estimators = n_estimators
def fit(self, X, y):
"""
AdaBoost 多分类SAMME.R算法拟合
"""
# 标签分类
self.classes = np.unique(y)
# 标签分类数
self.n_classes = len(self.classes)
# 初始化样本权重
sample_weights = np.ones(X.shape[0]) / X.shape[0]
# 估计器数组
estimators = []
# 论文中对 y 的定义
y_codes = np.array([-1. / (self.n_classes - 1), 1.])
# 将训练集中的标签值转换成论文中的矩阵形式
y_coding = y_codes.take(self.classes == y[:, np.newaxis])
# 遍历估计器
for i in range(self.n_estimators):
# 初始化最大深度为1的决策树估计器
estimator = DecisionTreeClassifier(max_depth = 1)
# 根据样本权重拟合训练集
estimator.fit(X, y, sample_weight=sample_weights)
# 预测训练集标签值的概率
y_predict_proba = estimator.predict_proba(X)
# 处理概率为0的结果,避免取对数是结果为负无穷大的问题
np.clip(y_predict_proba, np.finfo(y_predict_proba.dtype).eps, None, out=y_predict_proba)
# 计算样本权重
temp_weights = sample_weights * np.exp(- ((self.n_classes - 1) / self.n_classes) * np.sum(np.multiply(y_coding, np.log(y_predict_proba)), axis=1))
# 归一化样本权重
sample_weights = temp_weights / np.sum(temp_weights)
estimators.append(estimator)
self.estimators = estimators
def predict(self, X):
"""
AdaBoost 多分类SAMME.R算法预测
"""
# 结果集合
results = np.zeros((X.shape[0], self.n_classes))
# 遍历估计器
for i in range(self.n_estimators):
estimator = self.estimators[i]
# 预测标签值的概率
y_predict_proba = estimator.predict_proba(X)
# 同样需要处理零概率的问题
np.clip(y_predict_proba, np.finfo(y_predict_proba.dtype).eps, None, out=y_predict_proba)
# 对概率取对数
y_predict_proba_log = np.log(y_predict_proba)
# 计算 h(x)
h = (self.n_classes - 1) * (y_predict_proba_log - (1 / self.n_classes) * np.sum(y_predict_proba_log, axis=1)[:, np.newaxis])
# 累加
results += h
# 取累加最大对应的分类作为最后的结果
return self.classes.take(np.argmax(results, axis=1), axis=0)
使用 Python 实现 AdaBoost.R2 算法
import numpy as np
from sklearn.tree import DecisionTreeRegressor
class adaboostr():
"""
AdaBoost 回归算法
"""
def __init__(self, n_estimators = 100):
# AdaBoost弱学习器数量
self.n_estimators = n_estimators
def fit(self, X, y):
"""
AdaBoost 回归算法拟合
"""
# 初始化样本权重向量
sample_weights = np.ones(X.shape[0]) / X.shape[0]
# 估计器数组
estimators = []
# 估计器权重数组
weights = []
# 遍历估计器
for i in range(self.n_estimators):
# 初始化最大深度为3的决策树估计器
estimator = DecisionTreeRegressor(max_depth = 3)
# 根据样本权重拟合训练集
estimator.fit(X, y, sample_weight=sample_weights)
# 预测结果
y_predict = estimator.predict(X)
# 计算误差向量(线性误差)
errors = np.abs(y_predict - y)
errors = errors / np.max(errors)
# 计算误差率
e = np.sum(np.multiply(errors, sample_weights))
# 当误差率大于等于0.5时跳出循环
if e >= 0.5:
self.n_estimators = i
break
# 计算估计器权重
weight = e / (1 - e)
# 计算样本权重
temp_weights = np.multiply(sample_weights, np.power(weight, 1 - errors))
# 归一化样本权重
sample_weights = temp_weights / np.sum(temp_weights)
weights.append(weight)
estimators.append(estimator)
self.weights = np.array(weights)
self.estimators = np.array(estimators)
def predict(self, X):
"""
AdaBoost 回归算法预测
"""
# 论文中权重的定义
weights = np.log(1 / self.weights)
# 预测结果矩阵
predictions = np.array([self.estimators[i].predict(X) for i in range(self.n_estimators)]).T
# 根据预测结果排序后的下标
sorted_idx = np.argsort(predictions, axis=1)
# 根据排序结果依次累加估计器权重,得到新的累积权重矩阵,类似累积分布函数的定义
weight_cdf = np.cumsum(weights[sorted_idx], axis=1, dtype=np.float64)
# 累积权重矩阵中大于其中中位数的结果
median_or_above = weight_cdf >= 0.5 * weight_cdf[:, -1][:, np.newaxis]
# 中位数结果对应的下标
median_idx = median_or_above.argmax(axis=1)
# 对应的估计器
median_estimators = sorted_idx[np.arange(X.shape[0]), median_idx]
# 取对应的估计器的预测结果作为最后的结果
return predictions[np.arange(X.shape[0]), median_estimators]
六、第三方库实现
scikit-learn3 实现自适应增强分类
from sklearn.ensemble import AdaBoostClassifier
# 自适应增强分类器 SAMME 算法
clf = AdaBoostClassifier(n_estimators = 50, random_state = 0, algorithm = "SAMME")
# 自适应增强分类器 SAMME.R 算法
clf = AdaBoostClassifier(n_estimators = 50, random_state = 0, algorithm = "SAMME.R")
# 拟合数据集
clf = clf.fit(X, y)
scikit-learn4 实现自适应增强回归
from sklearn.ensemble import AdaBoostRegressor
# 自适应增强回归器
clf = AdaBoostRegressor(n_estimators = 50, random_state = 0)
# 拟合数据集
clf = clf.fit(X, y)
七、示例演示
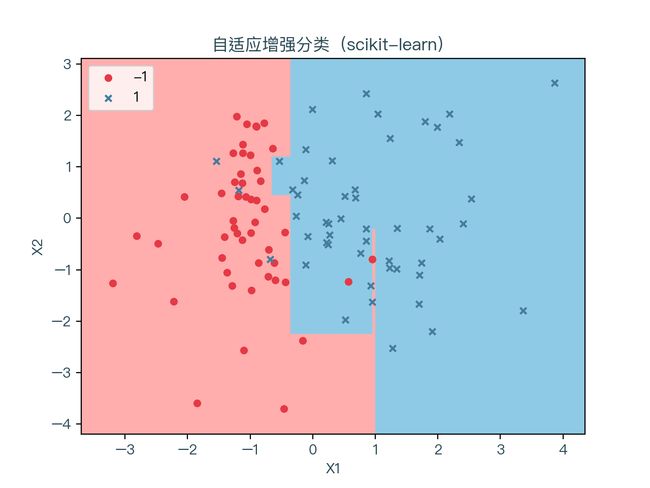
图 7-1 展示了使用自适应增强算法进行二分类的结果,红色表示标签值为 -1 的样本点,蓝色代表标签值为 1 的样本点。浅红色的区域为预测值为 -1 的部分,浅蓝色的区域则为预测值为 1 的部分
图 7-2 、图 7-3 分别展示了使用 SAMME 和 SAMME.R 算法进行多分类的结果,红色表示标签值为 0 的样本点,蓝色代表标签值为 1 的样本点,绿色代表标签值为 2 的样本点。浅红色的区域为预测值为 0 的部分,浅蓝色的区域则为预测值为 1 的部分,浅绿色的区域则为预测值为 1 的部分
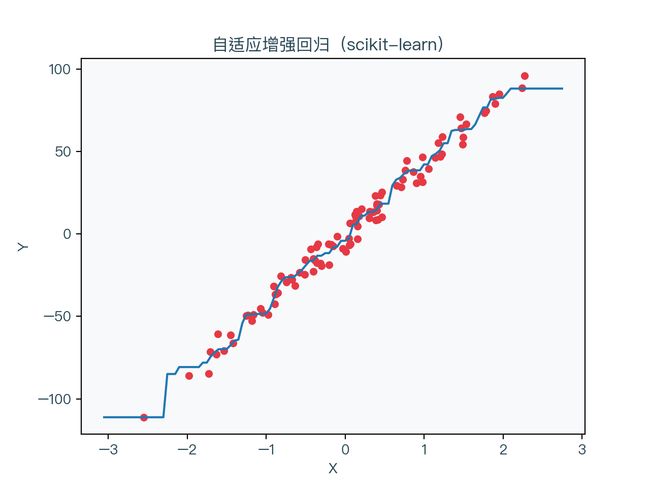
图 7-4 展示了使用自适应增强算法进行回归的结果
八、思维导图
九、参考文献
- https://en.wikipedia.org/wiki/Boosting_(machine_learning)
- https://en.wikipedia.org/wiki/AdaBoost
- https://scikit-learn.org/stable/modules/generated/sklearn.ensemble.AdaBoostClassifier.html
- https://scikit-learn.org/stable/modules/generated/sklearn.ensemble.AdaBoostRegressor.html
- https://www.face-rec.org/algorithms/Boosting-Ensemble/decision-theoretic_generalization.pdf
- https://citeseer.ist.psu.edu/viewdoc/download?doi=10.1.1.21.5683&rep=rep1&type=pdf
- https://hastie.su.domains/Papers/samme.pdf
完整演示请点击这里
注:本文力求准确并通俗易懂,但由于笔者也是初学者,水平有限,如文中存在错误或遗漏之处,恳请读者通过留言的方式批评指正
本文首发于——AI导图,欢迎关注