机器学习自学笔记——聚类
聚类的基本概念
聚类,顾名思义,就是将一个数据集中各个样本点聚集成不同的“类”。每个类中的样本点都有某些相似的特征。比如图书馆中,会把成百上千的书分成不同的类别:科普书、漫画书、科幻书等等,方便人们查找。每一种类别的书都有相似之处:比如科普书类别中的书基本上都是普及一些科学知识,这就是他们的相似之处。而聚类可以理解为“将一堆图书分为不同的类别的过程”。
这里不得不说明一下“聚类”和“分类”的区别:
- 聚类是刚创立一个图书馆,通过各种渠道获得了一堆图书,事先我不知道可以分为哪些类,但是随着分类的进行,逐渐被分为不同的类。这是一种无监督学习。
- 分类是现在有一堆图书,要将其按类别放入图书馆的书架上,这些类别都是事先确定的,比如科普类、文学类、历史类等等,按类别放入即可。这是一种监督学习。
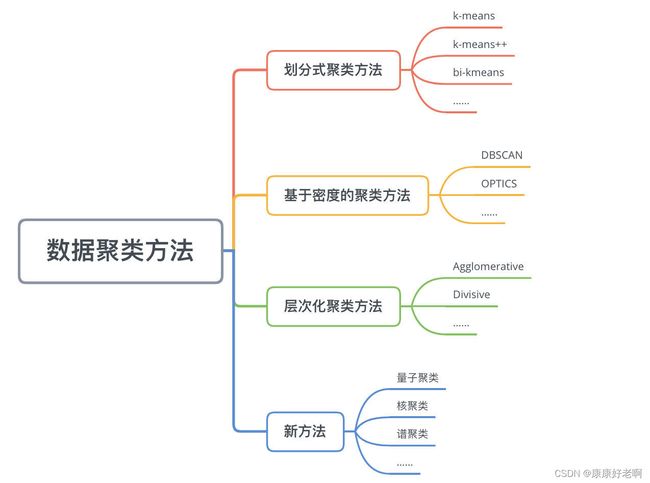
数据的聚类方法有很多,如下图:
本文之后会主要介绍k-means(k均值聚类)和层次聚类算法中的聚合聚类。
上面这些聚类算法有一些共同步骤:
- 数据准备:对数据进行特征标准化和降维处理。就像将事先准备好的一本本图书一本本堆叠规整放好
- 特征选择/提取:从最初的特征中选择最有效的特征,进行转换形成新的突出特征,并将其存储在向量中。就像将图书中十分破烂或者不良的剔除,并存储在专门存储图书的地方
- 进行聚类:基于某种距离函数进行相似度度量,并形成聚簇。就像按照某种规律(书名出现相同的字)将图书之间归类(都出现百科归一类、都出现秋天归一类······)
- 结果评估:对聚类的分类结果进行评估,判断聚类进行的优劣。就像将图书聚类完之后,抽取图书并翻看内容来判断其类别是否正确
相似度度量
在上面的聚类算法的步骤中,“进行聚类”这一步骤中出现了“相似度度量”,这也是聚类算法中最重要的点。比如像我用图书的例子进行类比时,在“进行聚类”这一步说得就十分不清楚,因为我没法找到一个合适的标准去衡量图书之间的相似程度。
在聚类算法中,我们会通过计算“距离”去衡量相似度。当我们将特征数字化之后,特征之间是否相似也就是特征数字之间是否大小接近。需要注意的是,这里的“距离”是广义距离,并不仅仅是我们通常理解的 d 1 − d 2 d_1-d_2 d1−d2这种距离。下面我们来看几种比较常见的距离:
1、闵可夫斯基距离
① 欧式距离
欧式距离就是我们最常见的距离度量方法,就是两点之间的最短距离。
假设两个点的坐标分别为 x 1 ( x 11 , x 12 , x 13 , ⋅ ⋅ ⋅ , x 1 n ) x_1(x_{11},x_{12},x_{13},···,x_{1n}) x1(x11,x12,x13,⋅⋅⋅,x1n), x 2 ( x 21 , x 22 , x 23 , ⋅ ⋅ ⋅ , x 2 n ) x_2(x_{21},x_{22},x_{23},···,x_{2n}) x2(x21,x22,x23,⋅⋅⋅,x2n),(我们也称 x 11 , x 12 , x 13 , ⋅ ⋅ ⋅ , x 1 n x_{11},x_{12},x_{13},···,x_{1n} x11,x12,x13,⋅⋅⋅,x1n为 x 1 x_1 x1的特征)则这两个点的欧式距离为:
L ( x 1 , x 2 ) = ∑ i = 1 n ( x 1 i − x 2 i ) 2 L(x_1,x_2)=\sqrt{\sum_{i=1}^n{(x_{1i}-x_{2i})^2}} L(x1,x2)=i=1∑n(x1i−x2i)2
② 曼哈顿距离
假设两个点的坐标分别为 x 1 ( x 11 , x 12 , x 13 , ⋅ ⋅ ⋅ , x 1 n ) x_1(x_{11},x_{12},x_{13},···,x_{1n}) x1(x11,x12,x13,⋅⋅⋅,x1n), x 2 ( x 21 , x 22 , x 23 , ⋅ ⋅ ⋅ , x 2 n ) x_2(x_{21},x_{22},x_{23},···,x_{2n}) x2(x21,x22,x23,⋅⋅⋅,x2n),则这两个点的曼哈顿距离为:
L ( x 1 , x 2 ) = ∑ i = 1 n ∣ x 1 i − x 2 i ∣ L(x_1,x_2)=\sum_{i=1}^n|x_{1i}-x_{2i}| L(x1,x2)=i=1∑n∣x1i−x2i∣
③ 切比雪夫距离
假设两个点的坐标分别为 x 1 ( x 11 , x 12 , x 13 , ⋅ ⋅ ⋅ , x 1 n ) x_1(x_{11},x_{12},x_{13},···,x_{1n}) x1(x11,x12,x13,⋅⋅⋅,x1n), x 2 ( x 21 , x 22 , x 23 , ⋅ ⋅ ⋅ , x 2 n ) x_2(x_{21},x_{22},x_{23},···,x_{2n}) x2(x21,x22,x23,⋅⋅⋅,x2n),则这两个点的切比雪夫距离为:
L ( x 1 , x 2 ) = ( ∑ i = 1 n ∣ x 1 i − x 2 i ∣ p ) 1 p L(x_1,x_2)=(\sum_{i=1}^n|x_{1i}-x_{2i}|^p)^{\frac{1}{p}} L(x1,x2)=(i=1∑n∣x1i−x2i∣p)p1
其中p趋于正无穷。
其实,上面三种计算方法可以进行一个统一,这就是这一部分的小标题——闵可夫斯基距离。欧氏距离是闵可夫斯基距离 L ( x 1 , x 2 ) = ( ∑ i = 1 n ∣ x 1 i − x 2 i ∣ p ) 1 p L(x_1,x_2)=(\sum_{i=1}^n|x_{1i}-x_{2i}|^p)^{\frac{1}{p}} L(x1,x2)=(∑i=1n∣x1i−x2i∣p)p1中 p = 2 p=2 p=2的结果,曼哈顿距离是该式 p = 1 p=1 p=1的结果,而切比雪夫距离是 p = + ∞ p=+\infin p=+∞的结果
2、马氏距离
马氏距离全称马哈拉诺比斯距离。样本不同的特征之间大小尺寸可能会不同,比如特征1两个数据为10000和20000,特征2两个数据为1和2。如果只考虑其距离,那么10000与12000之间相差的数字肯定要比1与2之间相差的数字要大,但这并不意味着前者的相似度一定要比后者更小,因为他们的尺寸不同难以比较,所以使用马氏距离可以避免这种问题:
d i j = [ ( x i − x j ) T S − 1 ( x i − x j ) ] 1 2 d_{ij}=[(x_i-x_j)^TS^{-1}(x_i-x_j)]^\frac{1}{2} dij=[(xi−xj)TS−1(xi−xj)]21
其中 x i x_i xi是样本 i i i的特征矩阵, x j x_j xj是样本 j j j的特征矩阵, S S S是样本集合 X X X的协方差矩阵。
3、相关系数
相关系数的定义表达式为:
r i j = ∑ k = 1 m ( x k i − x ‾ i ) ( x k j − x ‾ j ) [ ∑ k = 1 m ( x k i − x ‾ i ) 2 ∑ k = 1 m ( x k j − x ‾ j ) 2 ] 1 2 r_{ij}=\frac{\sum_{k=1}^{m}(x_{ki}-\overline x_i)(x_{kj}-\overline x_j)}{[\sum_{k=1}^{m}(x_{ki}-\overline x_i)^2\sum_{k=1}^{m}(x_{kj}-\overline x_j)^2]^\frac12} rij=[∑k=1m(xki−xi)2∑k=1m(xkj−xj)2]21∑k=1m(xki−xi)(xkj−xj)
相关系数越接近1,表示样本越相似;相关系数越接近0,表示样本越不相似。
4、夹角余弦
夹角余弦的定义表达式为:
s i j = ∑ k = 1 m x k i x k j [ ∑ k = 1 m x k i 2 ∑ k = 1 m x k j 2 ] 1 2 s_{ij}=\frac{\sum_{k=1}^{m}x_{ki}x_{kj}}{[\sum_{k=1}^{m}x_{ki}^2\sum_{k=1}^{m}x_{kj}^2]^\frac12} sij=[∑k=1mxki2∑k=1mxkj2]21∑k=1mxkixkj
夹角余弦越接近1,表示样本越相似;夹角余弦越接近0,表示样本越不相似。
上面的这些距离是样本点之间的距离,在聚类算法中,我们还需要一种衡量类与类之间的距离方法,常见的有以下四种:
(1)最短距离/单链接(Single-link):
定义两个类的样本之间的最短距离为两类之间的距离。
缺点:容易出现包含范围特别大的类,因为并没有对两个类的最大距离进行限制。
(2)最长距离/完全链接(Complete-link):
定义两个类的样本之间的最长距离为两类之间的距离。
缺点:容易受到异常样本点的影响而造成不合理的聚类,因为异常样本点很容易干扰最长距离。
(3)中心距离(UPGMA):
定义两个类的样本中心之间的距离为两类之间的距离。
(4)平均距离(WPGMA):
定义两个类任意样本之间的距离的平均为两类之间的距离。
聚合聚类
聚合聚类是一种层次聚类算法,主要分为两种:聚合聚类和分类聚类。聚合聚类开始将每个样本各自分到一个类之中,之后再讲相距最近的两个类合并,最终生成一个类;而分裂聚类正好相反,先将所有样本分到一个类之中,再将样本中距离最远的分到两个新的类。这里只介绍聚合聚类。
算法步骤:
- (1)计算样本两两之间的欧式距离,构造距离矩阵
- (2)将每个样本都变成一个类: G 1 , G 2 , ⋅ ⋅ ⋅ , G n G_1,G_2,···,G_n G1,G2,⋅⋅⋅,Gn
- (3)定义**最短距离(Single-link)**为类间距离,找出距离最小的两个类归为一个新的类
- (4)如果只剩下一个类,那么停止运算,否则继续重复(3)(4)
算法复杂度: O ( n 3 m ) O(n^3m) O(n3m), n n n是样本个数, m m m是样本维数
K均值聚类
K均值聚类是已知要将原数据样本分成k个类,但是并不知道这k个类具体是什么。刚开始要随机选取k个点作为样本的初始中心点,这k个点各自属于一个类别。再通过比较距离大小将剩余的点分到这k个点对应的类别之中。
算法步骤:
- (1)初始化,随机选取k个点作为初始的聚类中心,这k个点各属于一个类别
- (2)计算每个样本到聚类中心的距离,并将其归类到与其距离最近的类之中
- (3)通过对每个样本取均值计算每个类新的聚类中心(因为加入了新的点),重复(2)的操作
- (4)如果两次操作所得到的分类相同,则停止操作。否则继续重复(2)(3)的操作
算法的复杂度: O ( n m k ) O(nmk) O(nmk), n n n是样本个数, m m m是样本维数, k k k是类别个数