Vision MLP 之 Sparse-MLP A Fully-MLP Architecture with Conditional Computation

Vision MLP 之 Sparse-MLP A Fully-MLP Architecture with Conditional Computation

原始文档：https://www.yuque.com/lart/papers/pfvpvo

从摘要读文章

Mixture-of-Experts (MoE) with sparse conditional computation has been proved an effective architecture for scaling attention-based models to more parameters with comparable computation cost. In this paper, we propose Sparse-MLP, scaling the recent MLP-Mixer model with sparse MoE layers, to achieve a more computation-efficient architecture.

本文引入MoE的思想，使用条件计算来实现再扩充参数的同时，还可以保证计算成本不会太高。

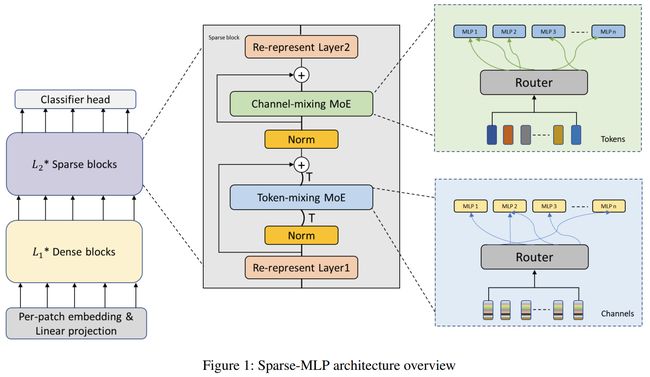
We replace a subset of dense MLP blocks in the MLP-Mixer model with Sparse blocks. In each Sparse block, we apply two stages of MoE layers:

1. one with MLP experts mixing information within channels along image patch dimension,
2. one with MLP experts mixing information within patches along the channel dimension.

对于空间MLP和通道MLP都会使用MoE进行改造。

Besides, to reduce computational cost in routing and improve expert capacity, we design Re-represent layers in each Sparse block. These layers are to re-scale image representations by two simple but effective linear transformations.

这里引入了放缩特征维度的结构降低计算量。

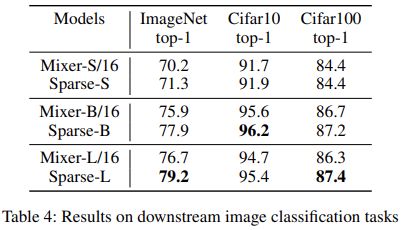
When pre-training on ImageNet-1k with MoCo v3 algorithm, our models can outperform dense MLP models by 2.5% on ImageNet Top-1 accuracy with fewer parameters and computational cost. On small-scale downstream image classification tasks, i.e., Cifar10 and Cifar100, our Sparse-MLP can still achieve better performance than baselines.

主要内容

• 将 MoE 技术引入 MLP 模型中，用于替换原始的 MLP 层。其中，通过构建多个具有不同权重的专家，从而扩大了模型的容量和表达能力，并且通过门控路由机制从而约束了实际使用的专家数量，即所谓的 conditional computation。从而不至于带来过多的计算成本和时间损耗。
• 由于原始空间 token 数量和通道数量差异较大，这会导致在路由和专家前向计算时不平衡的计算成本（computational cost），所以作者们在空间 MoE 层的前后通过对空间 token 数量和通道数量进行平衡（使用线形层重新投影），从而保证了更加平衡和有效的计算过程。

专家混合结构（Mixture of Experts)

核心操作

$\text{MoE}(x)={\sum }_{i=1}^{N}G(x{)}_i{E}_i(x),G(x)=\text{TopK}(\text{softmax}(W_g(x)+ϵ)):{\mathbb{R}}^D\to {\mathbb{R}}^N,E_i(x):{\mathbb{R}}^D\to {\mathbb{R}}^D.$

这里从左到右分别是包含 $N$ 个专家的 MoE 层的聚合操作，用于计算以输入为条件的路由权重的门控网络（使用 softmax 生成归一化权重，这里引入了噪声 $ϵ\sim \mathcal{N}(0,\frac{1}{N^2})$ 从而探索更好的分配策略），以及第 $i$ 个专家层。

相近工作

• MoE 的思想主要来自于 ICLR 2017 的一篇文章：OUTRAGEOUSLY LARGE NEURAL NETWORKS: THE SPARSELY-GATED MIXTURE-OF-EXPERTS LAYER (Noam Shazeer, Azalia Mirhoseini, Krzysztof Maziarz, Andy Davis, Quoc Le, Geoffrey Hinton and Jeff Dean)，该文提到“The capacity of a neural network to absorb information is limited by its number of parameters. Conditional computation, where parts of the network are active on a per-example basis, has been proposed in theory as a way of dramatically increasing model capacity without a proportional increase in computation.”。这篇文章通过在 LSTM 中间插入多个专家结构，通过可训练的门控网络来对专家们进行稀疏组合，从而将模型的能力（capacity）提升了超过 1000 倍并且只有少量的效率损失。除了主要的想法与这篇文章类似外，针对 MoE 结构的优化策略也基本一脉相承。
• 另外，这篇 SparseMLP 的工作与作者们的另一篇针对 ViT 改进的工作 Go Wider Instead of Deeper 有着潜在的共通点。

Go Wider Instead of Deeper

• 当然，从损失函数上来讲，其实更像 Scaling Vision with Sparse Mixture of Experts 这篇文章。损失函数形式非常相似。

本文细节

本文主要将 Mixer-MLP 中的最后几层空间和通道 MLP 进行了替换，替换成了 MoE 结构（包含空间和通道两种结构）。这样的设定有助于引入更多的参数，提升模型的能力。

多专家模型的训练是不容易的。主要是由于稀疏的门控路由机制导致并不是所有的专家必然可以被得到充分的训练，也就是所谓的负载不均衡问题。所以使用多专家设定的方法大多数都需要特殊的损失来进行针对性的处理。

对于损失函数，本文延续了之前工作的设定，应用了负载均衡损失（Load Balance Loss）。该损失鼓励横跨专家对输入进行均衡分配。

该损失包含两部分设定：

• 重要性损失（Importance Loss）：目的是让各个专家信息传播过程中的重要性尽量相近，这样可以保证各个专家可以被尽量选择到并被充分的训练。
  • 为此，引入了关于专家重要性的定义：$\text{Imp}(X)=\{{\sum }_{x\in X}\text{softmax}(W_{g}x{)}_i{\}}_{i=1}^N$。
  • 权重 $W_g\in {\mathbb{R}}^{D\times N}$ 表示 MoE 层的门控权重矩阵（gating weight matrix），其将输入的 $D$ 维的 $x$ 的映射到专家数量 $N$，由 softmax 处理后即获得每个样本 $x$ 被分配到各个专家的权重。这里将与第 $i$ 个专家有关的各个输入对应的权重加和后获得其对于 batch 输入 $X$ 的重要性度量。这可以反映出各个专家相较于其他专家，在整体输入被分配处理的过程中所起到的相对作用。
  • 所以为了尽可能均衡各个专家的重要性，使大家都能更好的“表现”，各个专家的重要性应该尽量均衡。于是使用重要性的平方变异系数（the squared coefficient of variation of the importance distribution over experts）作为重要性损失：$L_{imp}(X)=(\frac{\text{std}(\text{Imp}(X))}{\text{mean}(\text{Imp}(X))}{)}^2$。

论文Scaling Vision with Sparse Mixture of Experts的表 4

• 负载损失（Load Loss）：重要性损失旨在保证所有专家平均而言具有相似的路由权重。但是不幸的是，不难想到这些看上去有着总体趋于平衡的权重的路由配置，仍然有一小部分专家获得了所有分配（可见上表，虽然输入 1~4 对专家的权重之和均为 2，但是却在最终额选择中，仅仅只会选择到专家 1 和 3，而 2 则无法得到合适的学习）。
  • 为此这里引入了关于专家负载的定义：$\text{Load}(X)=\{{\sum }_{x\in X}{p}_i(x){\}}_{i=1}^N$。
  • $p_i(x):=Pr(G(x{)}_i>=threshol{d}_k(G(x)))$，表示专家 $i$ 在输入 batch 数据时，对各个样本而言被选中（门控路由大于阈值，即位于前 k 个最大权重的专家中）的概率和。
  • 这个概率看上去不太好搞定，但是作者们这里引入了一个正态分布的噪声，使得一切都可以计算了，大致如下式，最后是一个正态分布变量的概率的计算：
    $$p_i(x):=Pr(G(x{)}_i>=threshol{d}_k(G(x)))=Pr(W_g(x{)}_i+ϵ>=threshol{d}_k(W_g(x)+ϵ))=Pr(ϵ>=threshol{d}_k(W_g(x)+ϵ)-W_g(x{)}_i)$$
  • 负载损失则表示为负载分布的平方变异系数：$L_{Load}(X)=(\frac{\text{std}(\text{Load}(X))}{\text{mean}(\text{Load}(X))}{)}^2$。

所以 MoE 层损失为：$L_{aux}=\lambda (\frac{1}{2}{L}_{imp}+\frac{1}{2}{L}_{load})$。这里的超参数 $\lambda$ 用来控制辅助损失在鼓励跨专家路由的平衡，也保证不会压制（overwhelm）原始的模型损失。实际与之前的工作设置一样，都设为 0.01。按照之前的工作，这个参数对于性能的影响不太明显。

除了多专家层本身的设定，考虑到在原始的 MLP-Mixer 中，基于 patch 的 token 处理方式导致空间 token 数量小于通道数量的 1/3。这对于 MOEs，也就是空间层面上的 MoE 层而言，会导致路由部分与专家部分计算成本的不均衡。所以作者们引入了一个重表征层（re-present layer)来重新调整 MOEs 的输入和输出的空间和通道尺寸。其中主要是通过专门的线性层进行处理，伪代码如下：

实际中设置 $S_1=2S,C_1=C/2$。

这里包含两层，一个用于输出，一个用于输入。二者搭配，用于平衡二者中间包裹的 MOEs 的运算（降低 MOEs 运算时的通道数量并增加空间 patch 数量。

实验结果

We find that scaling MLP models in parameters and training them from scratch with limited training data will lead to an overfitting problem. Such finding is consistent with previous work on MLP models (Tolstikhin et al. 2021) and attention based models (Chen, Xie, and He 2021; Dosovitskiy et al. 2020; Xue et al. 2021).

In order to better obtain model capacity, we adopt MoCo v3 algorithm as our default self-supervised training algorithm (He et al. 2019; Chen et al. 2020b; Chen, Xie, and He 2021), and fine-tune models on downstream image classification tasks.

所有的模型都是使用 MoCo V3 自监督训练得来的

论文的消融实验主要讨论了以下四点：

• 专家数量的影响

这里是分别固定 MoEs 和 MoEc 来做实验的，可以看到，MoEs 的增加可以带来性能的提升。但是 MoEc 却会导致下降，作者们认为是造成了过拟合（关于增加针对通道特征的专家数量会导致过拟合的现象在作者们之前的工作Go Wider Instead of Deeper中也有体现）。

• 路由选择的专家的数量 K

这里针对不同的位置分别尝试了不同的 K 值，这里都是基于 B 结构进行的实验。可以看到，对于通道专家需要同时应用更多，而空间单个即可。

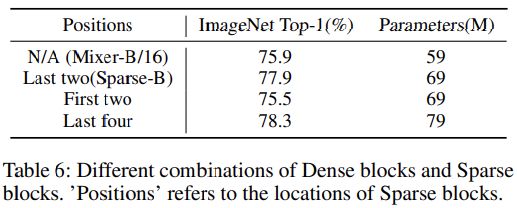
• Sparse Blocks 的位置，即 MoE 结构的位置

对于结构 B，原本 Sparse Blocks 被放置在最后两个阶段，这里进行了对比，可以看到，这样的结构放置到模型最后可以起到更好的效果。

• 重表征层的作用

可以看到，使用重表征层后虽然速度提升了，但是性能却没有下降，反而提升了。这是个有趣的现象。但是作者没有给出合理的解释和分析。仅仅是提了下其对于平衡路由和专家的计算成本的作用。那这样的结构直接用于 MLP-Mixer 中是否也会有提升？

参考链接

• Sparse-MLP: A Fully-MLP Architecture with Conditional Computation: https://arxiv.org/pdf/2109.02008.pdf
• OUTRAGEOUSLY LARGE NEURAL NETWORKS: THE SPARSELY-GATED MIXTURE-OF-EXPERTS LAYER: https://arxiv.org/pdf/1701.06538.pdf
• Go Wider Instead of Deeper: https://arxiv.org/pdf/2107.11817.pdf
• Scaling Vision with Sparse Mixture of Experts: https://arxiv.org/pdf/2106.05974.pdf