【优化选址】基于模拟退火结合粒子群算法求解分布式电源定容选址问题matlab源码

1 算法介绍

1.1 模拟退火算法

1.2 粒子群算法

粒子群算法同遗传算法相似，也是根据生物界中的种群行为而发明的一种算法。也是解决优化问题常用的一种算法。其原理简单，实现起来也不复杂，并且经过自己编程实践发现其速度要优于遗传算法。

粒子群算法源于鸟群觅食行为，假设有一群鸟，在随机搜索食物，在搜索区域内只有一块儿食物，一开始时所有的鸟儿都不知道食物所在的方位，但它们能够知道自己离食物有多远，以及它们能够记住在自己飞过的路程当中距离食物最近的位置，同时它们也能够知道鸟群中所有鸟儿经过的路程当中，离食物最近的位置。那每一只鸟儿将如何去寻找食物呢？简单来说，每一只鸟儿在当前位置的基础上，如何做出决策，下一步向哪里飞呢？实际，每只鸟儿将综合自身的经验，以及群体的经验来在做出下一步飞向哪里的决策，即每只鸟儿将根据自己所经过的路程中离食物最近的位置以及鸟群中所有鸟儿经过的路程当中离食物最近的位置来做出决策，决定下一步自己向哪里飞。这便是粒子群算法的基本原理

在粒子群算法中，粒子的位置对应于原问题的解。粒子的适应值就是将粒子的位置（对应于原问题的解）带入到目标函数中所得到的目标函数值。粒子的速度决定粒子下一步向哪里飞以及飞多远。

接下来先给在粒子群算法中最重要的两个公式：

在给出公式之前，先设定一些符号，

：代表优化问题在D维空间上的一个解，对应于粒子群中第i个粒子的位置

：代表第i个粒子所经历的所有路程上最优的位置，即其在飞翔过程中离目标函数最优解最近的位置

：代表所有粒子经历过的路程上的最优位置（可以认为是所有个体最优位置当中的最优位置）

：代表粒子i的飞翔速度

好了，接下来给出两个粒子群算法中的核心公式

公式一：

公式二：

在上面两个公式中，代表粒子编号；代表维度编号；为惯性因子，其取值范围为非负；为加速常数，其取值范围为非负常数；为0到1范围内的随机数；为约束因子，用来控制速度的权重。

需要说明的是，为了限制某个粒子的飞翔范围过大，我们为粒子的每一个维度设置一个最大飞翔速度，即如果粒子i在d维上的飞翔速度大于，则将这一维上的飞翔速度设置为，如果小于则将其设置为。的取值一般为对应维度所代表的决策变量取值范围的百分之十到百分之二十。例如设决策变量的取值范围为，则。

接下来对上文中的一些参数加以解释说明：

1.粒子数：粒子数的选取一般在20个到40个之间，但是需要具体问题具体对待，如果对于复杂问题，则需要设置更多的粒子，粒子数量越多，其搜索范围就越大。

2.惯性因子：用来控制继承多少粒子当前的速度的，越大则对于当前速度的继承程度越小，越小则对于当前速度的继承程度越大。有些同学可能会产生疑问，是不是说反了。其实不是，从公式中可以明确看出，其值越大，则速度的改变幅度就越大，则对于粒子的当前速度继承越小；反之，速度的改变幅度越小，则对于粒子当前速度继承越大。因此如果的值越大，则解的搜索范围越大，可以提高算法的全局搜索能力，但也损失了局部搜索能力，有可能错失最优解；反之如果的值越小，则解的搜索范围也就越小，算法的全局搜索能力也就越小，容易陷入局部最优。如果是变量，则其值应该随着迭代次数的增加而减小（类似于梯度下降当中的学习率）。如果为定值，则建议在0.6到0.75之间进行选取。

3.加速常数：通过公式一可以看出，加速常数控制着飞翔速度的计算是更加看重自身经验还是群体经验。公式一中的第二项就是自身经验的体现，加速常数可以看做是用来调整自身经验在计算粒子飞翔速度上的权重。同理是用来控制群体经验在计算粒子飞翔速度过程中的权重的。如果为0，则自身经验对于速度的计算不起作用，如果为0，则群体经验对于粒子飞翔速度的计算不起作用。的取值在学术界分歧很大主要有如下几种情况：

学者	和
Clerc
Carlisle
Trelea
Eberhart

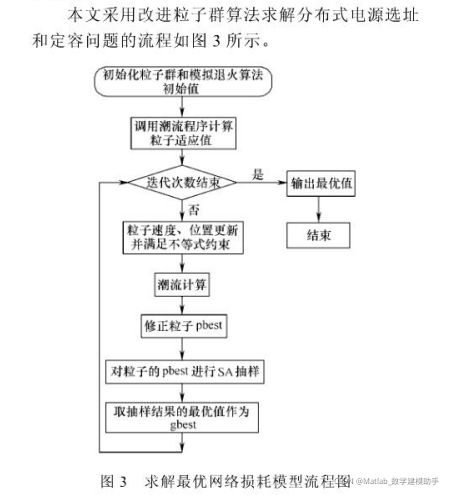
以下为粒子群算法的具体流程：

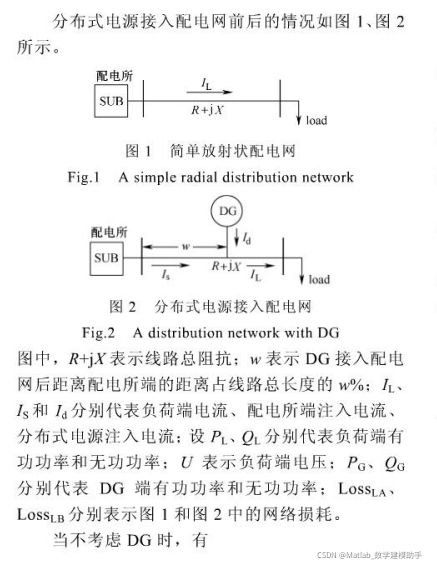
1.3 含有分布式电源的配电网结构

 

 

 

 

2 部分代码

%% 模拟退火粒子群算法分布式电源定容选址优化规划
tic                                                             %测试时间
format short ;
clc;
clear all;
%% 算法初始参数设置
pop=90;                                                         %种群粒子数目
gen=200;                                                         %最大迭代次数M
M=4;                                                            %目标函数个数
V=68;                                                           %控制变量个数
Xmax=10;                                                        %控制变量约束最大值
Xmin=0;                                                         %控制变量约束最小值
g_best=zeros(gen,V);                                            %全局最优存放位置
pop_num=40;                                                     %保存的最优前沿
lamda=0.5;                                                      %退火常数
%% 初始化种群个体
[pop_x,pop_v]=initial(pop,V,M);
%% 模拟退火粒子群算法
for t=1:gen                                                     %进入主要循环,gen迭代次数
                clear Gbest_value
                clear R
              %%  1.寻找全局最优
                [pbest,pbest_value,k]=gbest_fitness(pop_x,V,M,pop); 
                g_best(t,:)=pbest;
                g_best_value(t,:)=pbest_value;
              %% 1.对各目标函数值进行排序
                for j = 1 : M
                [Gbest_value(:,j),R(:,j)]=sort(g_best_value(:,j));
                end
               %% 2.根据个体排序计算其适应度
               for i = 1 : t
                  for j = 1 : M
                      if R(i,j)>1
                            ex(i,j)=(pop-R(i,j))^2;
                      else 
                            ex(i,j)=k*pop;  
                      end
                  end
               end
               ex=sum(ex');
             %% 3.得到适应度最好的全局最优解
               [Fit,index]=sort(ex');
               %[y_val,index]=min(g_best_value);
               clear Fit;
               gbest=g_best(index,:);
        %% 2.速度更新
               change_v=update_v(t,gen,pop_v,pop_x(:,1:68),g_best,V,pop,pbest);
               pop_v=change_v;
        %% 2.更新位置
               change_x=pop_x(:,1:V)+change_v(:,1:V);
        %% 控制变量约束

            for i = 1 : pop
                for j = 1 : V
            if change_x(i,j)>Xmax
                   change_x(i,j)=unidrnd(10);
            else if change_x(i,j) 
  
 
  
3 仿真结果
 
  
 
  
 
  
4 参考文献
 
  
[1]王艳敏. 基于可靠性的供应链设施选址问题的优化模型[J]. 科学技术与工程, 2012, 12(011):2517-2520.
 
  
5 代码下载