Python数据分析案例22——财经新闻可信度分析(线性回归，主成分回归，随机森林回归)

 本次案例还是适合人文社科领域，金融或者新闻专业。本科生做线性回归和主成分回归就够了，研究生还可以加随机森林回归，其方法足够人文社科领域的硕士毕业论文了。

---

案例背景

有八个自变量，['微博平台可信度','专业性','可信赖性','转发量','微博内容质量','时效性','验证程度','人际信任']   ，一个因变量： 投资信息可信度。

研究这八个自变量对因变量的影响。

---

数据读取

导入包

import numpy as np
import pandas as pd
import matplotlib.pyplot as plt 
import seaborn as sns
from sklearn.preprocessing import StandardScaler
import statsmodels.formula.api as smf
plt.rcParams ['font.sans-serif'] ='SimHei'               #显示中文
plt.rcParams ['axes.unicode_minus']=False               #显示负号
sns.set_style("darkgrid",{"font.sans-serif":['KaiTi', 'Arial']})

读取，我数据格式这里是spss 的sav格式，但是python也能读取。

# 读取数据清洗后的数据
spss = pd.read_spss('数据2.sav')
#spss

选取需要的变量，展示前五行

data=spss[['微博平台可信','专业性','可信赖性','转发量','微博内容质量','时效性','验证程度','人际信任','投资信息可信度']]
data.head()

取出列名称

columns1=data.columns

描述性统计，算一下均值方差分位数等等

data.describe()  #描述性统计

我这数据量并不多.... 

取出X和y

X=data.iloc[:,:-1]
y=data.iloc[:,-1]

 

---

画图展示

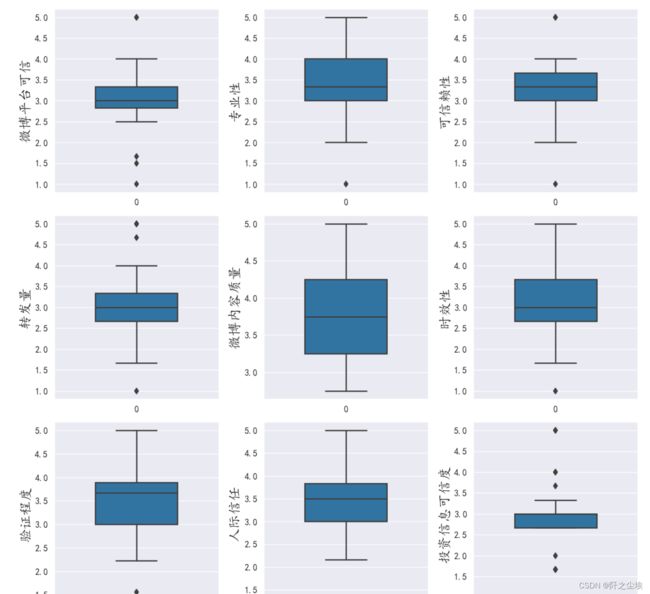
对八个自变量和一个因变量画箱线图 

column = data.columns.tolist() # 列表头
fig = plt.figure(figsize=(10,10), dpi=128)  # 指定绘图对象宽度和高度
for i in range(9):
    plt.subplot(3,3, i + 1)  # 2行3列子图
    sns.boxplot(data=data[column[i]], orient="v",width=0.5)  # 箱式图
    plt.ylabel(column[i], fontsize=16)
plt.tight_layout()
plt.show()

 

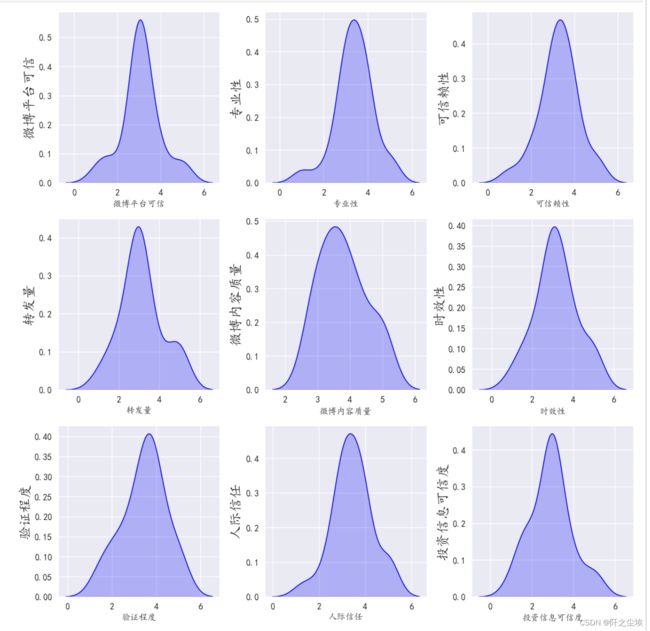
画核密度图

column = data.columns.tolist() # 列表头
fig = plt.figure(figsize=(10,10), dpi=128)  # 指定绘图对象宽度和高度
for i in range(9):
    plt.subplot(3,3, i + 1)  # 2行3列子图
    sns.kdeplot(data=data[column[i]],color='blue',shade= True)  
    plt.ylabel(column[i], fontsize=16)
plt.tight_layout()
plt.show()

 变量两两之间的散点图

sns.pairplot(data[column],diag_kind='kde')
#plt.savefig('散点图.jpg',dpi=256)

 变量之间的相关系数热力图

#画皮尔逊相关系数热力图
corr = plt.subplots(figsize = (14,14))
corr= sns.heatmap(data[column].corr(),annot=True,square=True)

 可以看到很多x之间的相关系数都挺高的，线性回归模型应该存在严重的多重共线性。

---

线性回归分析

导入包

import statsmodels.formula.api as smf

打印回归方程

all_columns = "+".join(data.columns[:-1])
print('x是：'+all_columns)
formula = '投资信息可信度~' + all_columns
print('回归方程为：'+formula)

拟合模型 

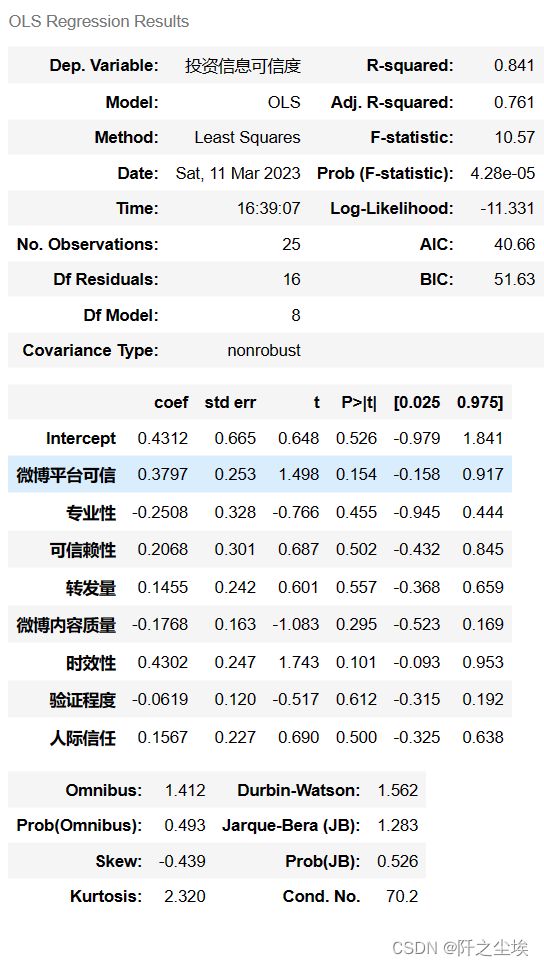
results = smf.ols(formula, data=data).fit()
results.summary()

 

 可以看到拟合优度还挺高，84%。再看每个变量的p值，0.05的显著性水平下，几乎都不显著.....

应该是多重共线性导致的。

还可以这样查看回归结果：

print(results.summary().tables[1])

系数p值什么的和上面一样。

对数回归 

在计量经济学里面有一种常用的手段就是将数据去对数，这样可以减小异方差等影响。我们来试试，取了对数再回归：

data_log=pd.DataFrame(columns=columns1)
for i in columns1:
    data_log[i]=data[i].apply(np.log)

拟合

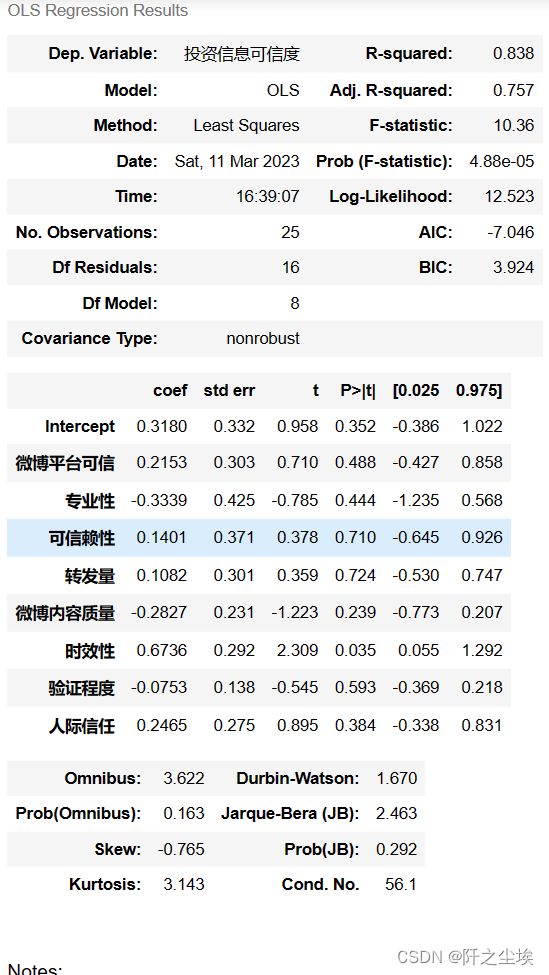
results_log = smf.ols(formula, data=data_log).fit()
results_log.summary()

 也好不到哪去....只有时效性的p值小于0.05，是显著的，别的都不显著。

接下来使用主成分回归

---

主成分回归

主成分回归会压缩你的变量，弄出几个新的变量，这样变量之间的多重共线性就能处理掉了。

新的变量就是老变量的线性组合，但是不好解释，失去了经济或者新闻上的实际意义。

导包

from sklearn.decomposition import PCA
from sklearn.model_selection import cross_val_score
from sklearn.linear_model import LinearRegression
from sklearn.model_selection import LeaveOneOut
from mpl_toolkits import mplot3d

想找一下几个主成分回归，要用几个主成分会好一些：

model = PCA()
model.fit(X)
#每个主成分能解释的方差
model.explained_variance_
#每个主成分能解释的方差的百分比
model.explained_variance_ratio_
#可视化
plt.plot(model.explained_variance_ratio_.cumsum(), 'o-')
plt.xlabel('Principal Component')
plt.ylabel('Cumulative Proportion of Variance Explained')
plt.axhline(0.9, color='k', linestyle='--', linewidth=1)
plt.title('Cumulative PVE')

可以看到当主成分个数为4时就能解释原始数据的90%以上了（坐标轴上是3是因为从0 开始的..）

 下面采用四个主成分进行回归分析：

将X转化为4个主成分矩阵，查看数据形状。

model = PCA(n_components = 4)
model.fit(X)
X_train_pca = model.transform(X)
X_train_pca.shape

 

25是我的样本量，4是主成分个数。（25个确实少了....） 

 变成数据框：（主成分得分矩阵）

columns = ['PC' + str(i) for i in range(1, 5)]
X_train_pca_df = pd.DataFrame(X_train_pca, columns=columns)
X_train_pca_df.head()

上面只展示了前5行。

还可以计算主成分核载矩阵，显示了原始变量和主成分之间的关系。

pca_loadings= pd.DataFrame(model.components_.T, columns=columns,index=columns1[:-1])
pca_loadings

 

 打印主成分回归方程

X_train_pca_df['财经信息可信度']=y
all_columns = "+".join(X_train_pca_df.columns[:-1])
print('x是：'+all_columns)
formula = '财经信息可信度~' + all_columns
print('回归方程为：'+formula)

拟合模型

results = smf.ols(formula, data=X_train_pca_df).fit()
results.summary()

 

 只有第一个和第四个主成分是显著的。

打印查看：

print(results.summary().tables[1])

 主成分回归效果也一般。

这种传统的统计学模型——参数模型，线性模型，限制和假定太多了，不好用。

一遇见多重共线性，异方差等问题就G了

 下面采用非参数的回归方法——随机森林，可以避免多重共线性的影响，得到变量的重要特征排序。

---

 

随机森林回归

像随机森林，支持向量机，梯度提升这种机器学习模型放在人文社科领域都是降维打击。人文社科领域用的还是老一套的传统统计学模型，效果都不太好。

随机森林回归在统计、计算机等学科里面都是很简单的模型了，但若在人文社科学科，这种模型写在论文里面肯定算高级的了。

先将数据标准化

# 数据标准化
from sklearn.preprocessing import StandardScaler
scaler = StandardScaler()
scaler.fit(data)
data = scaler.transform(data)
data[:5]

 取出X和y

airline_scale = data
airline_scale.shape

X=airline_scale[:,:-1]
y=airline_scale[:,-1]
X.shape,y.shape

 拟合模型：

from sklearn.ensemble import RandomForestRegressor
model = RandomForestRegressor(n_estimators=5000, max_features=int(X.shape[1] / 3), random_state=0)
model.fit(X,y)
model.score(X,y)

上面这段代码生成了一个含有5000棵决策树的随机森林模型，拟合，评价。

拟合优度高达95%！！ 

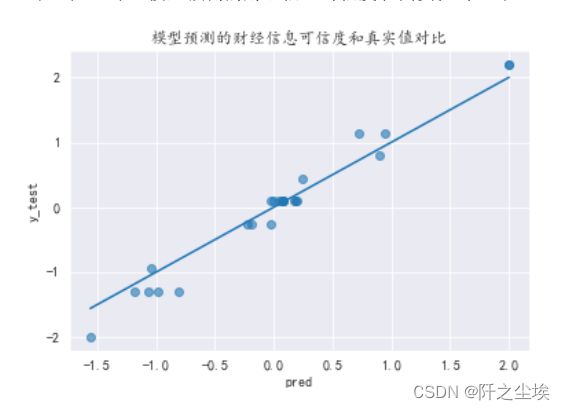
查看真实值和拟合值对比的图：

pred = model.predict(X)
plt.scatter(pred, y, alpha=0.6)
w = np.linspace(min(pred), max(pred), 100)
plt.plot(w, w)
plt.xlabel('pred')
plt.ylabel('y_test')
plt.title('模型预测的财经信息可信度和真实值对比')

 

 很接近。

计算变量的重要性：

model.feature_importances_
sorted_index = model.feature_importances_.argsort()

plt.barh(range(X.shape[1]), model.feature_importances_[sorted_index])
plt.yticks(np.arange(X.shape[1]), columns1[:-1][sorted_index],fontsize=14)
plt.xlabel('Feature Importance',fontsize=14)
plt.ylabel('Feature')
plt.title('特征变量的重要性排序图',fontsize=24)
plt.tight_layout()

可以看到，对于 投资信息可信度这样因变量，信息的时效性，转发量，平台可信度是最重要的，其次就是人际信任，可信赖性等等变量。

上面是每个变量对于y的重要性，

下面画出每个变量分别是怎么影响y的，偏依赖图：

X2=pd.DataFrame(X,columns=columns1[:-1])
from sklearn.inspection import PartialDependenceDisplay
#plt.figure(figsize=(12,12),dpi=100)
PartialDependenceDisplay.from_estimator(model, X2,['时效性','转发量','微博平台可信'])
#画出偏依赖图

我们可以很清楚得看到，时效性，转发量，微博平台可信度，三个变量的取值变化是怎么影响y的变化的，明显不是一个线性的关系，虽然大致的方向是正相关，但是影响的程度是一个非线性的关系，先慢后快再慢。

---

总结 

本次用了三种方法做了一个财经新闻领域的回归问题，每个方法都有优缺点吧，但是效果肯定还是机器学习的模型好。有的同学肯定在想机器学习模型怎么没有p值什么的，怎么看显不显著？

其实机器学习的方法没有参数估计和假设检验的，没有p值什么的，所以做不了统计推断，这也是它的一个缺点。传统的线性回归，主成分回归，虽然可以统计推断，但是效果很差。

看每个人的需求做什么样的模型了，但是在人文社科的论文写一歌机器学习的模型还是算得上创新吧。