堆排序、快速排序、归并排序算法详解
目录
堆排序
堆的概念
实现堆排序
堆排序的时间复杂度：
快速排序
概念
第一种：挖坑法
第二种：左右指针法
第三种：快慢指针
分治递归实现整体有序
非递归算法实现整体有序（了解）
归并排序
堆排序
堆的概念
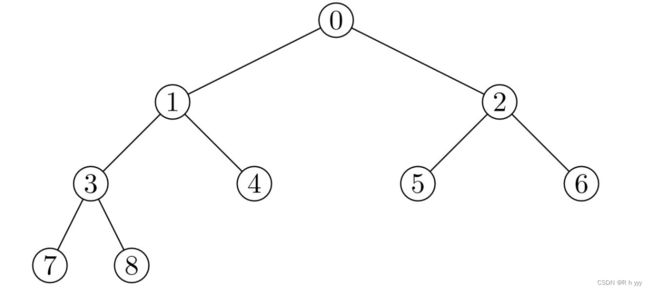
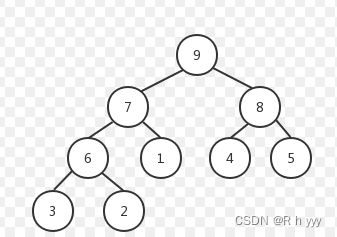
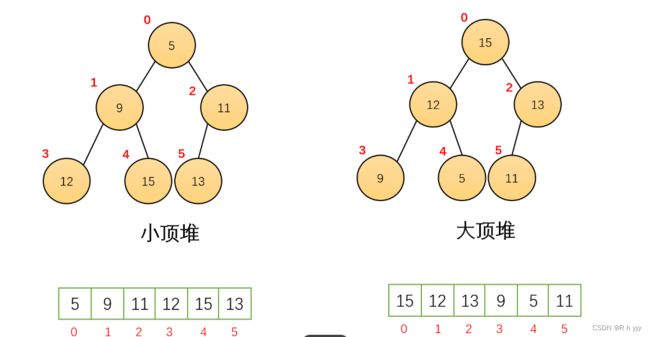
学会使用堆排序首先了解堆的概念，堆是一个由数组储存的完全二叉树，它的逻辑结构是一颗二叉树，物理结构是一个数组。且任意子树的root的值是其左孩子和右孩子的值的最大值或最小值。堆分为大堆小堆，大堆：堆顶数据最大，小堆：堆顶数据最小。
小堆如下所例：
大堆如下：
由于堆是由数组顺序储存所以我们可轻松索引到某个节点。
堆中 父亲和儿子的下标关系为：
leftchild == parent*2 + 1 ; rightchild == parent*2 + 2 == leftchild + 1 ;
parent == ( child - 1 ) / 2 ;
实现堆排序
第一步是建堆：
自底向上的方式建一个大堆（排升序）或建一个小堆（排降序），从最后一个非叶子节点（最后一个父亲节点）开始调整。
以建大堆为例：
实现原理：向下调整算法，在一任意一颗二叉树中若parent的值比child小，则将两个child中大的数值与parent互换，直到该二叉树中所有子树都满足大堆即可
//交换两个节点的值
void swap(int *p1, int*p2)
{
int tmp = *p1;
*p1 = *p2;
*p2 = tmp;
}
//向下调整算法 实现大堆
void ADjustDown(int *arr, int n, int root)
{
int parent = root;
int child = root * 2 + 1;
while (child < n)
{
if (child+1< n && (arr[child] < arr[child + 1])) //（child+1）注意越界、选出两个child中较大的值
{
child += 1;
}
if (arr[child] > arr[parent])
{
swap(&arr[child], &arr[parent]);
parent = child;
child = parent * 2 + 1;
}
else
{
break;
}
}
}
//实现堆排序
void HeapSort(int *arr, int n)
{
for (int i = (n - 1 - 1) / 2; i >= 0;--i) //自底向上 从最后一个parent节点开始调整，依次往上
{
ADjustDown(arr, n, i);
}//循环走完 建堆完成
//实现排序
int end = n - 1;
while (end > 0)
{
swap(&arr[end], &arr[0]); //将堆顶的数（该数组中最大的数）放到数组的组后一个位置
ADjustDown(arr, end, 0); //继续向下调整，实现大堆
end--;
}
//循环走完，排序完成
}堆排序的时间复杂度：
建堆的时间复杂度O(n),排序选数的时间复杂度为O（logN），所有最终时间复杂度为N*logN。是一个非常高效的排序算法。
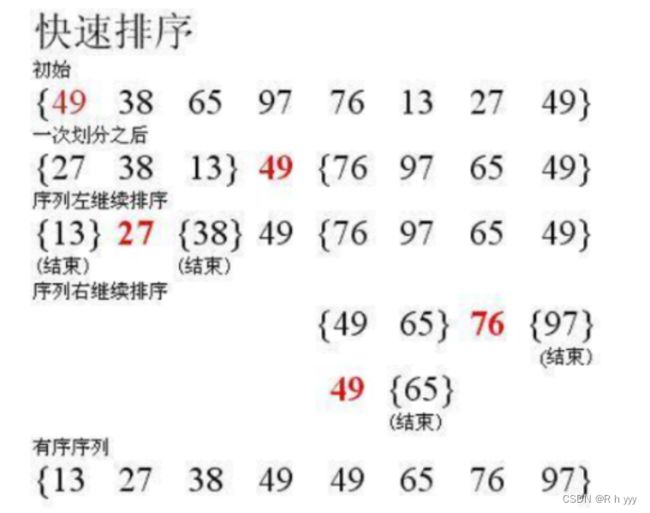
快速排序
概念
快速排序是 Hoare 于 1962 年提出的一种二叉树结构的交换排序方法，其基本思想为：任取待排序
元素序列中的某元素作为基准值，按照该排序码将待排序集合分割成两子序列，左子序列中所有
元素均小于基准值，右子序列中所有元素均大于基准值，然后最左右子序列重复该过程，直到所
有元素都排列在相应位置上为止。
（单趟排序）将区间按照基准值划分为左右两半部分的常见方式有三种：
第一种：挖坑法
先从该数列中选出一个基准值（key），并设key值的位置为坑（pivot）
end先向左走，若找到比key小的值就往（坑）pivot里放，该数挪走了又出现一个新的坑，begin又向右走找到比key大的值就向坑里放，又会出现一个新的坑。循环下去，最终begin<=end时，将key值放到最后一个坑中去，最后实现key左边的都比key小，右边的都比key大，完成单趟排序。
//单趟排序 挖坑法
int PartSort1(int *arr,int left,int right)
{
int begin = left;
int end = right;
int index = GetMidindex(arr, left, right);
swap(&arr[begin], &arr[index]);
int key = arr[begin];
int pivot = begin;
//循环内实现左边小 右边大
while (begin < end)
{
while (begin < end && arr[end] >= key)
{
--end;
}
arr[pivot] = arr[end];
pivot = end;
while (begin < end && arr[begin] <= key)
{
++begin;
}
arr[pivot] = arr[begin];
pivot = begin;
}
pivot = begin;
arr[pivot] = key;
return pivot;
}第二种：左右指针法
思想和上述方法类似，但是不需要设pivot挖坑，采用交换的方式实现左边小右边大。
先从该数列中选出一个基准值的下标（keyi），end先向左走，找比keyi位置的值小的，在begin向右走找到比keyi位置大的值，然后交换begin和end的值，循环下去，begin=end最后将keyi和begin互换，达到同样的效果。
//左右指针法 细节缺陷较多
int PartSort2(int *arr, int left ,int right)
{
int begin = left;
int end = right;
int index = GetMidindex(arr, left, right);
swap(&arr[left], &arr[index]);
int keyi = begin;
while (begin < end)
{
//end找小 while (begin=arr[keyi])
{
--end;
}
//begin找大
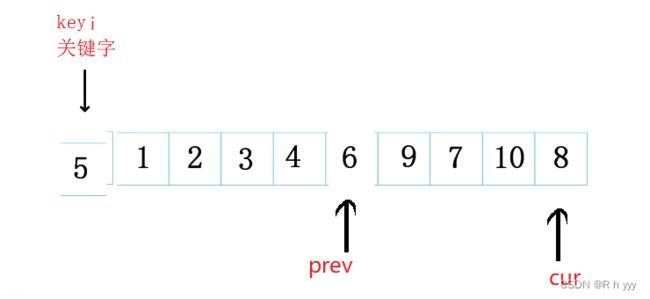
while (begin 第三种：快慢指针
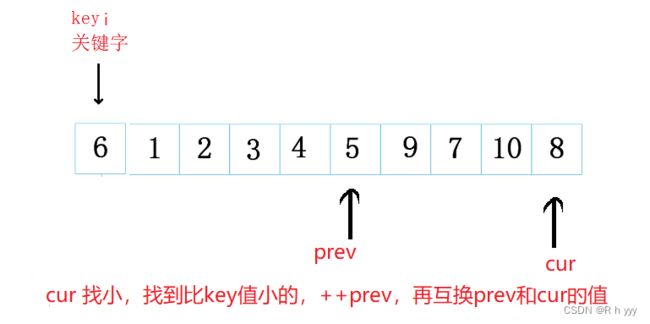最后cur=n-1时，再将prev和keyi互换，完成单趟排序
//单趟排序 快慢指针法方便好用！
int PartSort3(int*arr, int left, int right)
{
int prev = left;
int cur = left + 1;
int index = GetMidindex(arr, left, right);
swap(&arr[left], &arr[index]);
int keyi = left;
while (cur <= right)
{
//升序cur找比arr[keyi]小交换，降序cur找大交换
if (arr[cur] < arr[keyi])
{
++prev;
swap(&arr[prev], &arr[cur]); //通过prev使大的值往后扔
}
++cur;
}
swap(&arr[prev], &arr[keyi]);
return prev;
}分治递归实现整体有序
最后实现整体排序，使用分治递归的思想，当左子区间有序，右子区间有序则该数组有序。将左右子区间继续分割，最终当区间中只有一个值时则该子区间有序。
//递归实现
void QuickSort(int*arr, int left,int right)
{
if (left >= right) //区间只有一个值时
return;
int indexkey = PartSort3(arr, left, right);
//以下递归 为分治算法 满足key左区间有序 右区间有序，则该数组有序
QuickSort(arr, left, indexkey - 1);
QuickSort(arr, indexkey + 1, right);
}非递归算法实现整体有序（了解）
通过数据结构中的栈模拟操作系统中栈帧
//非递归 实现快速排序
void QuickSortNonR(int*arr, int n)
{
Stack st;
StackInit(&st);
StackPush(&st,n-1); //将数组的左右区间 压入栈中
StackPush(&st, 0);
while (!StackEmpty(&st))
{
int left=StackTop(&st);
StackPop(&st);
int right=StackTop(&st);
StackPop(&st);
int indexkey = PartSort2(arr, left, right);
//如果被分子区间元素个数大于2 则继续入栈 出栈 操作
//[left,indexkey-1] [indexkey+1,right]
if (indexkey + 1 < right)
{
StackPush(&st, right);
StackPush(&st, indexkey+1);
}
if (left < indexkey - 1)
{
StackPush(&st,indexkey-1);
StackPush(&st, left);
}
}
StackDestory(&st);
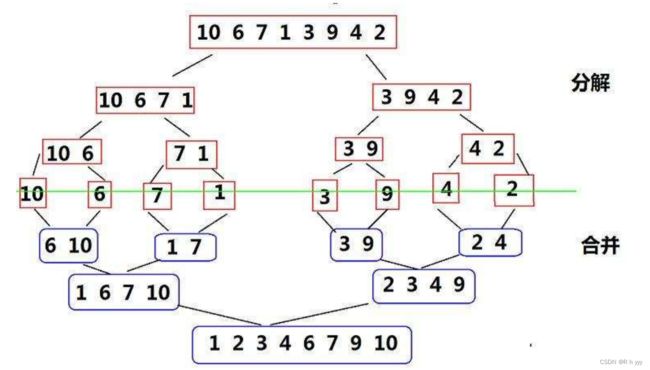
}归并排序
基本思想：
归并排序（ MERGE-SORT ）是建立在归并操作上的一种有效的排序算法 , 该算法是采用分治法
（ Divide and Conquer ）的一个非常典型的应用。将已有序的子序列合并，得到完全有序的序
列；即先使每个子序列有序，再使子序列段间有序。若将两个有序表合并成一个有序表，称为二
路归并。 归并排序核心步骤：
代码实现
//归并排序
void _MergeSort(int*arr, int left, int right, int*tmp)
{
if (left >= right)
{
return;//该子区间只有一个数时
}
//分治 对半分解数组
int mid = (left + right) >> 1;
_MergeSort(arr, left, mid, tmp);
_MergeSort(arr, mid + 1, right, tmp);
//按升序归并
int index = left;
int begin1 = left, end1 = mid;
int begin2 = mid + 1, end2 = right;
while (begin1 <= end1 && begin2 <= end2)
{
if (arr[begin1] < arr[begin2]) //选大的向临时数组中拷贝
{
tmp[index++] = arr[begin1++];
}
else
{
tmp[index++] = arr[begin2++];
}
}
while (begin1 <= end1)//当右区间归完，左区间还没归完时
{
tmp[index++] = arr[begin1++];
}
while (begin2 <= end2)//当左区间归完，右区间还没归完时
{
tmp[index++] = arr[begin2++];
}
//将临时数组的数据拷贝到原数组
for (int i = 0; i <= right; i++)
{
arr[i] = tmp[i];
}
}
void MergeSort(int*arr, int n)
{
int*tmp = (int*)malloc(sizeof(int)*n); //创建一个临时数组用来存放排好序的数
_MergeSort(arr,0, n-1, tmp);
free(tmp);
} 归并排序的特性总结：
1. 归并的缺点在于需要 O(N) 的空间复杂度，归并排序的思考更多的是解决在磁盘中的外排序问
题。
2. 时间复杂度： O(N*logN)
3. 空间复杂度： O(N)
4. 稳定性：稳定