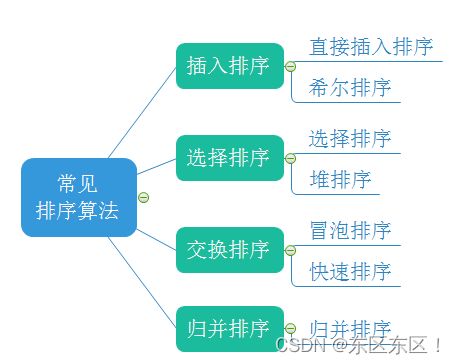
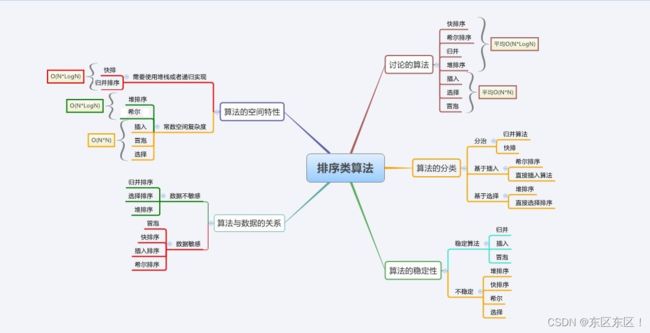
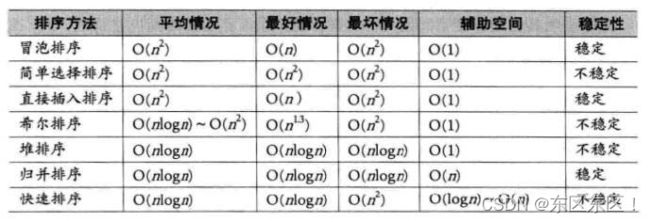
【数据结构】排序(3)归并排序及所有排序总结
今天学习排序最后一节,归并排序,这也是数据结构的最后一节学习内容,完了之后就会进入C++的学习,数据结构说难也不难,给我感觉就是,在上课学习的时候内容思想基本上能听懂,但是过一段时间就会忘记,所以还是要勤于复习。
目录
总结
一、归并排序
1.思路
2. 分析时间空间复杂度及稳定性
3.循环的归并排序
4.归并排序实际中的应用场景
二、非比较排序(简单了解)
1. 计数排序(鸽巢原理)
总结放在前面吧,经常需要复习
总结
一、归并排序
基本思想:建立在归并操作上的一种有效排序算法,来源于分治法。
将以有序的子序列合并,得到完全有序的序列 即先使每个子序列有 序,再使子序列段间有序。若将两个有序表合并成一个有序表,称为二路归并
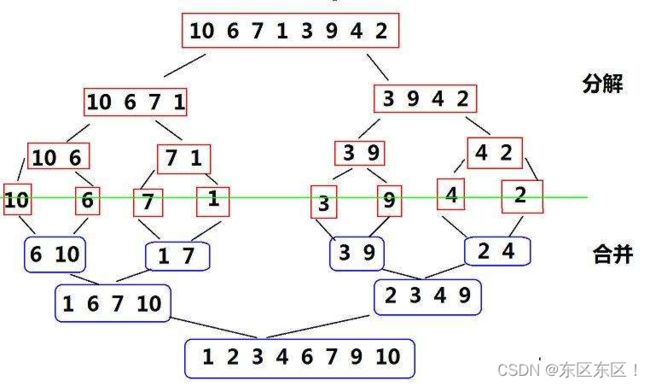
1.思路
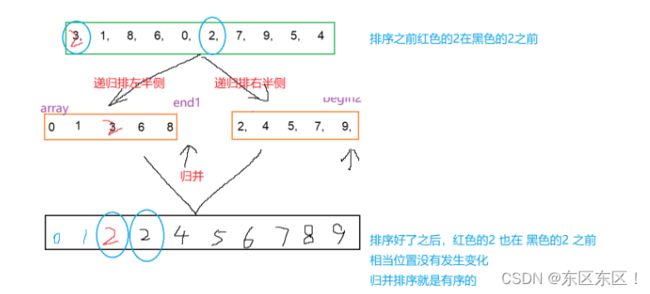
1.将区间中的元素划分为左右均等的两部分 [left, mid) 和 [ mid , right)
int mid = left + ((right - left)>> 1);坐半侧: [left, mid) 有半侧:[ mid , right)
2.递归将左半侧右半侧排好
3.将左半侧 和右半侧 两个有序的序列归并为一个
void MergeSort(int array[], int size)
{
int* temp = (int*)malloc(sizeof(int)*size);
if (NULL == temp)
{
assert(0);
return;
}
_MergeSort(array, 0, size, temp);
free(temp);
}利用递归进行排序,最后进行合并
void _MergeSort(int array[], int left, int right, int* temp)
{
if (right - left <= 1)
return;
// 先将区间均分成两部分
int mid = left + ((right - left) >> 1);
// 递归排左半侧[left, mid)
_MergeSort(array, left, mid, temp);
// 递归排右半侧[mid, right)
_MergeSort(array, mid, right, temp);
// 将有序的左半侧[left, mid) 和 有序的右半侧[mid, right) 合并成一个
MergeData(array, left, mid, right, temp);
memcpy(array + left, temp + left, (right - left)*sizeof(int));
}将两个有序的区间归并成一个
void MergeData(int array[], int left, int mid, int right, int* temp)
{
// 左半侧
int begin1 = left;
int end1 = mid;
// 右半侧
int begin2 = mid;
int end2 = right;
int index = left;
// 将两个区间中的元素从前往后依次比较,将较小的元素往temp中搬移
while (begin1 < end1 && begin2 < end2)
{
if (array[begin1] <= array[begin2])
temp[index++] = array[begin1++];
else
temp[index++] = array[begin2++];
}
// 将另外一个区间中剩余的元素搬移到temp中
while (begin1 < end1)
{
temp[index++] = array[begin1++];
}
while (begin2 < end2)
{
temp[index++] = array[begin2++];
}
}2. 分析时间空间复杂度及稳定性
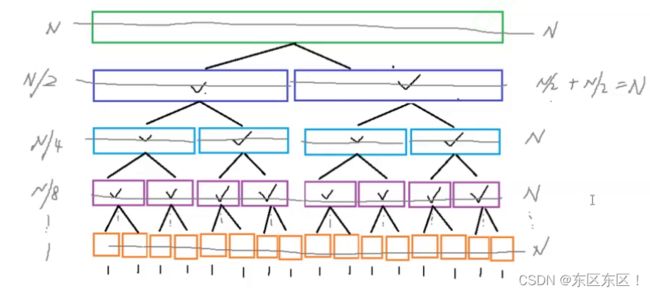
归并排序图划分好之后,一定是二叉平衡树的结构
因为每次都是将区间均分, 平衡二叉树就是 logN -->层数
每一层要处理N个数据
时间复杂度: O(NlogN)
空间复杂度:在整个排序过程中需要借助N个元素的辅助空间
整个递归过程的空间复杂度:O(N + logN)有多个阶项目取最高阶项。
空间复杂度:O(N)
稳定性:稳定
应用场景:归并的缺点在于需要O(N)的空间复杂度,归并排序的思考更多的是解决在磁盘中的外排序问题
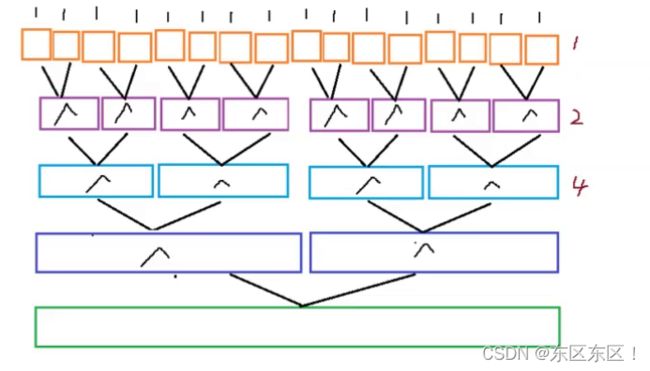
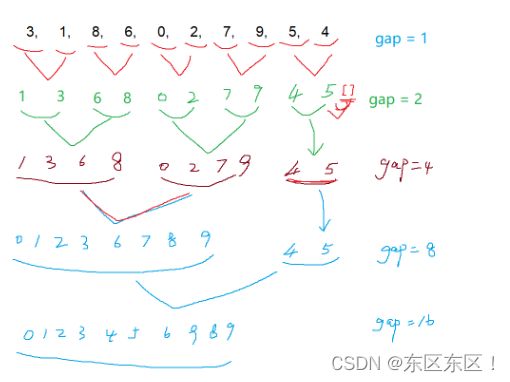
3.循环的归并排序
整体思路就是将上面归并排序的合并,利用设置gap,控制gap来进行循环合并,直到实现排序
void MergeSortNor(int array[], int size)
{
int* temp = (int*)malloc(sizeof(int)*size);
if (NULL == temp)
{
assert(0);
return;
}
int gap = 1;
while (gap < size)
{
for (int i = 0; i < size; i += 2*gap)
{
// 每个区间中有gap个元素
// [left, mid) 和 [mid, right)
int left = i;
int mid = left + gap;
int right = mid + gap;
// 注意加完gap之后,mid和right可能会越界
if (mid > size)
mid = size;
if (right > size)
right = size;
// [left, mid) 和 [mid, right)进行归并
MergeData(array, left, mid, right, temp);
}
memcpy(array, temp, sizeof(int)*size);
gap <<= 1; //左移一位,就是*2
}
free(temp);
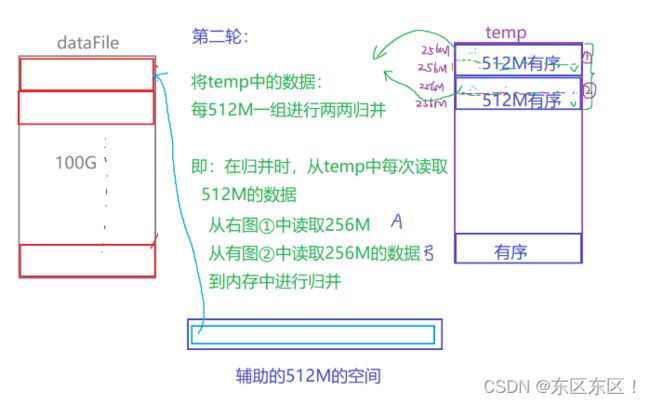
}4.归并排序实际中的应用场景
归并是外部排序,应用场景是数据量非常大无法一次加载到内存中去
二、非比较排序(简单了解)
1. 计数排序(鸽巢原理)
场景:数据密集集中在某个范围之内
1.统计每个元素出现的次数---统计好了次数需要保存起来的
需要知道数据的范围,一般会告诉范围
时间复杂度:O(N) N表示元素的个数
空间复杂度: O(M) M就是区间中元素的个数
稳定性:稳定的
应用场景:数据密集集中在某个范围内
1.比如数据集中在90-99之间,那么就不需要统计数据的范围,否则要先统计范围
2.计算用来保存计数空间的大小: range = maxvalue - minvalue + 1;
3.统计每个元素出现的次数:用每个元素—最小值 = 他的下标
例如:在下面这个数组中,90---》即数组0号位置,91--》为数组1号位置
4.按照计数数组的下标来进行回收
计数数组每个位置存储的数字是多少,则表明对应的数字出现了多少次
void CountSort(int array[], int size)
{
// 1. 假设没有告诉区间中数据的范围,如果告诉了第一步就不需要
// 统计数据的范围
// 比如:数据密集集中在某个范围内---此时就需要统计范围
// 数据秘密集中在90~99之间,就不需要统计范围
int minValue = array[0];
int maxValue = array[0];
for (int i = 0; i < size; ++i)
{
if (array[i] < minValue)
minValue = array[i];
if (array[i] > maxValue)
maxValue = array[i];
}
// 2. 计算需要多少个保存计数的空间
int range = maxValue - minValue + 1;
int* countArray = (int*)calloc(range, sizeof(int));
// 3. 统计每个元素出现的次数
for (int i = 0; i < size; ++i)
{
countArray[array[i] - minValue]++;
}
// 4. 按照统计的结果对数据进行回收
int index = 0;
for (int i = 0; i < range; ++i)
{
while (countArray[i] > 0)
{
array[index] = i + minValue;
countArray[i]--;
index++;
}
}
free(countArray);
}
2.其他