数据结构与算法--线性表（1）顺序表的实现

顺序表的基本定义

顺序表：线性表的顺序表示指的是用一组地址连续的存储单元依次存储线性表的数据元素，这种也称作线性表的顺序存储结构或顺序映像。通常称这种存储结构的线性表为顺序表，其特点是，逻辑上相邻的数据元素，其物理次序也是相邻的。

线性表中第i+1个数据元素的存储位置LOC(ai+1)和第i 个元素满足下列关系

顺序表的存储结构

只要确定了存储线性表的起始位置，线性表中任一数据元素都可随机存取，所以线性表的顺序存储结构是一种随机存取的存储结构，由于数组类型也有随机存取的特性，因此通常用数组来描述数据结构中的顺序存储结构。

#define MAXSIZE 100
typedef int ElemType;
typedef struct _Sqlist{
	ElemType* elem;	//存储空间基地址，即数组首地址
	int length;		//数组长度
}Sqlist;			//重命名顺序表的结构类型名

顺序表的基本操作

顺序表的初始化

初始化：顺序表的初始化就是构造一个空的顺序表

Status InitList(Sqlist& L){
	//构造一个空的顺序表L
	L.elem = new ElemType[MAXSIZE];	//为顺序表L动态分配一个大小为MAXSIZE的数组空间
	if (!L.elem) return OVERFLOW;	//若分配失败则退出
	L.length = 0;					//设置当前表长度为0
	return OK;
}

动态分配线性表的存储区域可以更有效地利用系统资源，当不需要该线性表时，可以使用销毁操作及时释放占用的存储空间。

顺序表的取值

Status GetElem(Sqlist L, int i, ElemType& e) {//通过引用"&"可以对实参地址进行操作，从而实现全局赋值
	if (i<1 || i>L.length) return ERROR;	//判断i是否在数组的空间范围内,若不合理返回ERROR
	e = L.elem[i - 1];			//elem[i-1]单元存储第i个数据元素
	return OK;
}

算法分析：取值算法的时间复杂度为O(1)。

顺序表的查找

//顺序表的按值查找
int LocateElem(Sqlist L, ElemType e) {
	//
	for (int i = 0; i < L.length; i++)
		if (L.elem[i] == e) return i + 1; //数组下标加1,返回表中位置
	return 0;
}

算法分析：在查找一个数据元素是，其时间主要耗费在数据比较上，而比较次数又取决于被查元素在线性表中的位置。
平均查找长度(ASL)
在查找时，为确定元素在顺序表中的位置，需和给定值进行比较的数据元素的个数的期望值称为查找算法在查找成功时的平均查找长度(Average Serach Length)

在此算法中，每个数据元素查找的概率相等，因此pi=1/n.

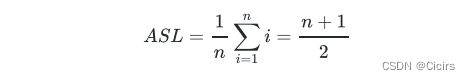
因此，顺序表按值查找算法的平均复杂度为O(n)

顺序表的插入

//顺序表的插入
Status ListInsert(Sqlist& L, int i, ElemType e) {
	//在顺序表L中第i个位置插入新的元素e
	if ((i < 1) || (i > L.length + 1)) return ERROR;	//i值不在表的区间，不合法
	if (L.length == MAXSIZE)	return ERROR;	//数组存储空间已满
	for (int j=L.length-1;j>=i-1;i--)  
		L.elem[j + 1] = L.elem[j];		//将第n至第i（包括插入位置）的元素依次向后移一位		
	L.elem[i - 1] = e;					//将新元素e放入第i个位置
	++L.length;							//表长加1
	return OK;
}

算法分析：在顺序表的插入算法中，其时间主要耗费在移动元素上，而移动元素的个数取决于插入元素的位置，因此可以通过计算插入一个元素时所需移动元素次数的期望值Eins（加权平均值）进行分析

为了使模型具有普遍性，假定在线性表的任意位置插入元素都是等概率的（即权重相等），即pi=1/(n+1)，则式子简化为：

因此，顺序表插入算法平均时间复杂度为O(n)。

顺序表的删除

//顺序表的删除
Status ListDelete(Sqlist& L, int i) {
	//在顺序表L中删除第i个元素
	if ((i < 1) || i > (L.length)) return ERROR; //	i值不在表内，不合法
	for (int j = i; j <= L.length - 1;j++)
		L.elem[j-1]=L.elem[j];			//被删除元素之后的元素前移
	--L.length;							//表长减一
	return OK;
}

算法分析：如上，其时间主要耗费在移动元素上，移动元素的个数取决于删除元素的位置，因此通过计算在长度为n的线性表中删除一个元素时所需移动元素的期望值Edel分析平均时间复杂度。

同样，为使模型具有普遍性，假定在线性表的任意位置删除元素都是等概率的，即pi=1/n，因此顺序表的删除算法的平均时间复杂度为O(n)。

销毁、清空、检查为空

//销毁、清空、检查为空
Status ClearSql(Sqlist& L) {
	//清空顺序表
	L.length = 0;
	return OK;
}
Status SqlDestroy(Sqlist* L) {
	//销毁顺序表
	if (!L->elem) return ERROR;
	else {
		free(L->elem);	//释放数组首地址
		return OK;
	}
}
Status SqlIsEmpty(Sqlist& L) {
	//检查为空
	if (0 == L.length)
		return TRUE;
	else 
		return FALSE;
}

顺序表的头文件

#ifndef _SQUENCELIST_H_
#define _SQUENCELIST_H_

#define TRUE 1
#define FALSE 0
#define OK 1
#define ERROR 0
#define INFEASIBLE -1


#define MAXSIZE 100
typedef int Status;

typedef int ElemType;
typedef struct _Sqlist{
	ElemType* elem;	//存储空间基地址，即数组首地址
	int length;		//数组长度
}Sqlist;			//重命名顺序表的结构类型名

//顺序表初始化
Status InitList(Sqlist& L);
//顺序表取值
Status GetElem(Sqlist L, int i, ElemType& e);
//顺序表的查找
int LocateElem(Sqlist L, ElemType e);
//顺序表的插入
Status ListInsert(Sqlist& L, int i, ElemType e);
//顺序表的删除
Status ListDelete(Sqlist& L, int i);
//销毁、清空、检查为空
Status ClearSql(Sqlist& L);
Status SqlDestroy(Sqlist* L);
Status SqlIsEmpty(Sqlist& L);
	
#endif

顺序表函数文件

#include "SequenceList.h" 
#include <iostream>
using namespace std;


//顺序表初始化
Status InitList(Sqlist& L){
	//构造一个空的顺序表L
	L.elem = new ElemType[MAXSIZE];	//为顺序表L动态分配一个大小为MAXSIZE的数组空间
	if (!L.elem) return OVERFLOW;	//若分配失败则退出
	L.length = 0;					//设置当前表长度为0
	return OK;
}

//顺序表取值
Status GetElem(Sqlist L, int i, ElemType& e) {//通过引用"&"可以对实参地址进行操作，从而实现全局赋值
	if (i<1 || i>L.length) return ERROR;	//判断i是否在数组的空间范围内,若不合理返回ERROR
	e = L.elem[i - 1];			//elem[i-1]单元存储第i个数据元素
	return OK;
}

//顺序表的按值查找
int LocateElem(Sqlist L, ElemType e) {
	//
	for (int i = 0; i < L.length; i++)
		if (L.elem[i] == e) return i + 1; //数组下标加1
	return 0;	//代表查询失败
}

//顺序表的插入
Status ListInsert(Sqlist& L, int i, ElemType e) {
	//在顺序表L中第i个位置插入新的元素e
	if ((i < 1) || (i > L.length + 1)) return ERROR;	//i值不在表的区间，不合法
	if (L.length == MAXSIZE)	return ERROR;	//数组存储空间已满
	for (int j=L.length-1;j>=i-1;i--)  
		L.elem[j + 1] = L.elem[j];		//将第n至第i（包括插入位置）的元素依次向后移一位		
	L.elem[i - 1] = e;					//将新元素e放入第i个位置
	++L.length;							//表长加1
	return OK;
}

//顺序表的删除
Status ListDelete(Sqlist& L, int i) {
	//在顺序表L中删除第i个元素
	if ((i < 1) || i > (L.length)) return ERROR; //	i值不在表内，不合法
	for (int j = i; j <= L.length - 1;j++)
		L.elem[j-1]=L.elem[j];			//被删除元素之后的元素前移
	--L.length;							//表长减一
	return OK;
}

//销毁、清空、检查为空
Status ClearSql(Sqlist& L) {
	//清空顺序表
	L.length = 0;
	return OK;
}
Status SqlDestroy(Sqlist* L) {
	//销毁顺序表
	if (!L->elem) return ERROR;
	else {
		free(L->elem);	//释放数组首地址
		return OK;
	}
}
Status SqlIsEmpty(Sqlist& L) {
	//检查为空
	if (0 == L.length)
		return TRUE;
	else 
		return FALSE;
}