预训练语言模型(GPT,BERT)
文章目录
- GPT 模型
-
- 预训练语言模型
- 模型和学习
- BERT 模型
-
- 去噪自编码器
- 模型和学习
- 模型特点
- References
在自然语言处理中事先使用大规模语料学习基于 Transformer 等的语言模型,之后用于各种任务的学习和预测,称这种模型为预训练语言模型。代表性的模型有 BERT (bidirectional encoder representations from Transformers)和 GPT (generative pre-training)。BERT 的模型是 Transformer 的编码器。首先在预训练中使用大规模语料通过掩码语言模型化的方法估计模型的参数,之后在微调中使用具体任务的标注数据对参数进行进一步调节。前者的过程是无监督学习,后者的过程是监督学习。GPT 的模型是 Transformer 的解码器,预训练通过一般的语言模型化方式进行。
GPT 模型
预训练语言模型
预训练语言模型的基本想法如下:基于神经网络,如 Transformer 的编码器或解码器,实现语言模型,以计算语言的生成概率。首先使用大规模的语料通过无监督学习的方式学习模型的参数,称为预训练,得到的模型可以有效地表示自然语言的特征;之后将模型用于一个具体任务,使用少量的标注数据通过监督学习的方式进一步学习模型的参数,称为微调,任务称为下游任务(downstream task)。预训练使用通用的语料统一进行,微调使用各个下游任务的标注数据分别进行。微调的模型有时在预训练模型的基础上增加新的参数。
下表比较了 GPT 和 BERT 的主要特点,其主要区别在于模型的架构和预训练方式。
| GPT | BERT | |
|---|---|---|
| 语言模型类型 | 单向语言模型 | 双向语言模型 |
| 模型架构 | Transformer 解码器 | Transformer 编码器 |
| 预训练方式 | 语言模型化 | 掩码语言模型化 |
| 预训练原理 | 序列概率估计 | 去噪自编码器 |
| 下游任务 | 语言理解、语言生成 | 语言理解 |
GPT 是单向语言模型,从一个方向对单词序列建模,方向为从左到右或者从右到左。假设有单词序列 x = x 1 , x 2 , ⋯ , x n \bm{x}=x_1,x_2,\cdots,x_n x=x1,x2,⋯,xn,在单词序列的各个位置上,单向语言模型具有以下单词生成的条件概率
P ( x i ∣ x 1 , x 2 , ⋯ , x i − 1 ) , i = 1 , 2 , ⋯ , n P(x_i|x_1,x_2,\cdots,x_{i-1}),\quad i=1,2,\cdots,n P(xi∣x1,x2,⋯,xi−1),i=1,2,⋯,n 每一个位置的单词依赖于之前位置的单词。可以使用单向语言模型计算单词序列 x = x 1 , x 2 , ⋯ , x n \bm{x}=x_1,x_2,\cdots,x_n x=x1,x2,⋯,xn 的生成概率。
BERT 是双向语言模型,从两个方向同时对单词序列建模。在单词序列的各个位置上,双向语言模型具有以下单词生成的条件概率
P ( x i ∣ x 1 , x 2 , ⋯ , x i − 1 , x i + 1 , ⋯ , x n ) , i = 1 , 2 , ⋯ , n P(x_i|x_1,x_2,\cdots,x_{i-1},x_{i+1},\cdots,x_n),\quad i=1,2,\cdots,n P(xi∣x1,x2,⋯,xi−1,xi+1,⋯,xn),i=1,2,⋯,n 每一个位置的单词依赖于之前位置和之后位置的单词。
GPT 的预训练通过语言模型化(language modeling)的方式进行,基于序列概率估计。对给定的单词序列 x = x 1 , x 2 , ⋯ , x n \bm{x}=x_1,x_2,\cdots,x_n x=x1,x2,⋯,xn,计算以下负对数似然函数或交叉熵,并通过其最小化估计模型的参数:
− log P ( x ) = − ∑ i = 1 n log P θ ( x i ∣ x 1 , x 2 , ⋯ , x i − 1 ) -\log P(\bm{x})=-\sum_{i=1}^n \log P_{\bm{\theta}} (x_i|x_1,x_2,\cdots,x_{i-1}) −logP(x)=−i=1∑nlogPθ(xi∣x1,x2,⋯,xi−1)
BERT 的预训练主要通过掩码语言模型化的方式进行,可以认为基于去噪自编码器。假设单词序列 x = x 1 , x 2 , ⋯ , x n \bm{x}=x_1,x_2,\cdots,x_n x=x1,x2,⋯,xn 中有若干个单词被随机掩码,也就是被改写为特殊字符
− log P ( x ˉ ∣ x ~ ) ≈ − ∑ i = 1 n δ i log P θ ( x i ∣ x ~ ) -\log P(\bar{\bm{x}}|\tilde{\bm{x}}) \approx -\sum_{i=1}^n \delta_i \log P_{\bm{\theta}} (x_i|\tilde{\bm{x}}) −logP(xˉ∣x~)≈−i=1∑nδilogPθ(xi∣x~) 其中, δ i \delta_i δi 取值为 1 或 0,表示是否对位置 i i i 的单词进行掩码处理。
BERT 只能用于语言理解,语言理解是对自然语言进行分析的处理,如文本分类、文本匹配、文本序列标注。
模型和学习
模型
GPT 模型有以下结构。输入是单词序列 x 1 , x 2 , ⋯ , x n x_1,x_2,\cdots,x_n x1,x2,⋯,xn,可以是一个句子或一段文章。首先经过输入层,产生初始的单词表示向量的序列,记作矩阵 H ( 0 ) \bm{H}^{(0)} H(0):
H ( 0 ) = X + E \bm{H}^{(0)} = \bm{X} + \bm{E} H(0)=X+E 其中, X \bm{X} X 表示单词的词嵌入的序列 X = ( x 1 , x 2 , ⋯ , x n ) \bm{X}=(\bm{x}_1,\bm{x}_2,\cdots,\bm{x}_n) X=(x1,x2,⋯,xn),矩阵 E \bm{E} E 表示单词的位置嵌入的序列 E = ( e 1 , e 2 , ⋯ , e n ) \bm{E}=(\bm{e}_1,\bm{e}_2,\cdots,\bm{e}_n) E=(e1,e2,⋯,en)。 X , E , H ( 0 ) \bm{X}, \bm{E}, \bm{H}^{(0)} X,E,H(0) 是 d × n d\times n d×n 矩阵,设词嵌入和位置嵌入向量的维度是 d d d。
之后经过 L L L 个解码层,得到单词表示向量的序列,记作矩阵 H ( L ) \bm{H}^{(L)} H(L):
H ( L ) = transformer_decoder ( H ( 0 ) ) \bm{H}^{(L)} = \text{transformer\_decoder}(\bm{H}^{(0)}) H(L)=transformer_decoder(H(0)) 具体地, H ( L ) = ( h 1 ( L ) , h 2 ( L ) , ⋯ , h n ( L ) ) \bm{H}^{(L)} = \left(\bm{h}_1^{(L)},\bm{h}_2^{(L)},\cdots,\bm{h}_n^{(L)}\right) H(L)=(h1(L),h2(L),⋯,hn(L))
其中, h i ( L ) \bm{h}_i^{(L)} hi(L) 是第 i i i 个位置的单词表示向量。GPT 模型中,在每一层,每一个位置的表示向量是该位置的单词基于之前位置的上下文表示。
GPT 模型的输出是在单词序列各个位置上的条件概率,第 i i i 个位置的单词的条件概率 p i p_i pi 定义为
P θ ( x i ∣ x 1 , x 2 , ⋯ , x i − 1 ) = softmax ( W x ⊤ h i ( L ) ) P_{\bm{\theta}} (x_i|x_1,x_2,\cdots,x_{i-1})=\text{softmax}(\bm{W}_x^\top \bm{h}_i^{(L)}) Pθ(xi∣x1,x2,⋯,xi−1)=softmax(Wx⊤hi(L)) 其中 W x \bm{W}_x Wx 表示所有单词的权重矩阵。
下图显示的是 GPT 模型的架构。GPT 利用 Transformer 解码器对语言的内容进行层次化的组合式的表示。
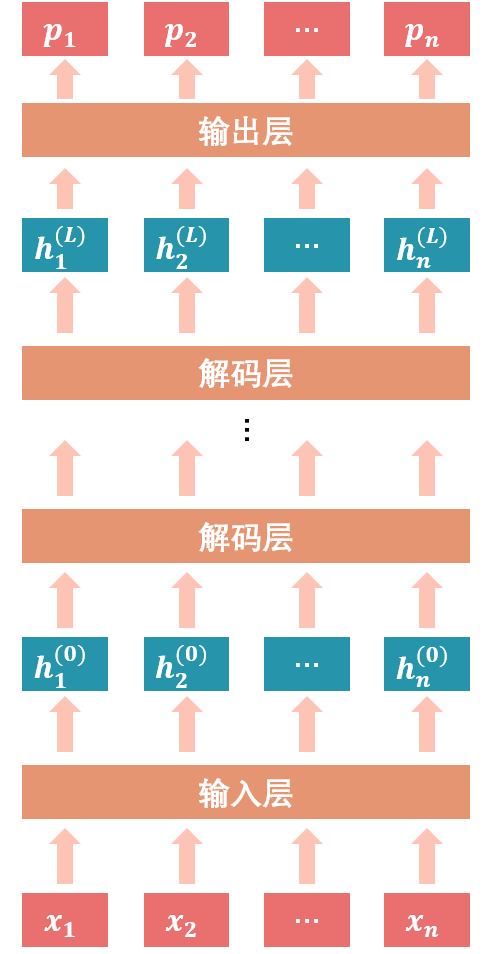
GPT 中解码层的多头自注意力都是单向的,也就是各个位置的单词只针对之前所有位置的单词进行自注意力计算。
预训练
预训练时,估计模型的参数,使模型对单词序列数据有准确的预测。预训练估计得到的参数作为下游任务模型的初始值。整个预训练通过 Transformer 解码器的学习进行。
微调
微调时,进一步调节参数,使模型对下游任务有准确的预测。假设下游任务是文本分类,输入单词序列 x ′ = x 1 , x 2 , ⋯ , x m \bm{x}' = x_1,x_2,\cdots,x_m x′=x1,x2,⋯,xm,输出类别是 y y y,计算条件概率
P θ , ϕ = ( y ∣ x 1 , x 2 , ⋯ , x m ) = softmax ( W y ⊤ h m ( L ) ) P_{\bm{\theta,\phi}} = (y|x_1,x_2,\cdots,x_m) = \text{softmax}(\bm{W}_y^\top \bm{h}_m^{(L)}) Pθ,ϕ=(y∣x1,x2,⋯,xm)=softmax(Wy⊤hm(L)) ϕ \phi ϕ 表示分类的参数。
损失函数包括两部分
L F T = L C L S + λ ⋅ L L M L_{FT}=L_{CLS} + \lambda \cdot L_{LM} LFT=LCLS+λ⋅LLM 一个是分类的损失函数 L C L S = − log P θ , ϕ ( y ∣ x ′ ) L_{CLS} = -\log P_{\bm{\theta,\phi}} (y|\bm{x}') LCLS=−logPθ,ϕ(y∣x′)
另一个是语言模型化的损失函数
L L M = − ∑ j = 1 m log P θ ( x j ∣ x 1 , x 2 , ⋯ , x j − 1 ) L_{LM} = -\sum_{j=1}^m \log P_{\bm{\theta}} (x_j|x_1,x_2,\cdots,x_{j-1}) LLM=−j=1∑mlogPθ(xj∣x1,x2,⋯,xj−1)
如果下游任务是生成,针对输入单词序列,进一步调节模型的参数,使得模型对之有准确的预测。损失函数只有语言模型化的部分。
GPT 是单向语言模型,用于语言理解时没有优势。因为语言理解中,输入是一个句子或一段文章,从两个方向同时对语言建模更加合理。BERT 可以解决这个问题。
BERT 模型
去噪自编码器
自编码器是用于数据表示的无监督学习的一种神经网络。自编码器由编码器和解码器网络组成。学习时,编码器将输入向量 x \bm{x} x 转换为中间表示向量 z \bm{z} z,解码器再将中间表示向量转换为输出向量 y \bm{y} y。假设 x \bm{x} x 和 y \bm{y} y 的维度相同,而 z \bm{z} z 的维度远低于 x \bm{x} x 和 y \bm{y} y 的维度。学习的目标是尽量使输出向量和输入向量保持一致,则认为学到的中间表示 z \bm{z} z 就是数据 x \bm{x} x 的表示。
自编码器学习实际进行的是对数据的压缩,得到的中间表示能有效地刻画数据的特征。因为通过解压可以得到原始数据的近似,说明中间表示保留了数据中的主要信息。
去噪自编码器是自编码器的扩展,学习时在输入中加入随机噪声,以学到稳健的自编码器。
学习时,首先根据条件概率分布 P ( x ~ ∣ x ) P(\bm{\tilde{x}}|\bm{x}) P(x~∣x) 对输入向量 x \bm{x} x 进行随机变换,得到有噪声的输入向量 x ~ \bm{\tilde{x}} x~。最基本的情况下,编码器、解码器、目标函数分别是
z = F ( x ) = a ( W E x ~ + b E ) \bm{z} = F(\bm{x}) = a(\bm{W}_E \bm{\tilde{x}}+\bm{b}_E) z=F(x)=a(WEx~+bE) y = G ( z ) = a ( W D z + b D ) \bm{y} = G(\bm{z}) = a(\bm{W}_D \bm{z}+\bm{b}_D) y=G(z)=a(WDz+bD) L = 1 N ∑ i = 1 N L ( x i , y i ) = 1 N ∑ i = 1 N L ( x i , G ( F ( x ~ i ) ) ) L=\frac{1}{N}\sum_{i=1}^N L(x_i,y_i)=\frac{1}{N}\sum_{i=1}^N L(x_i,G(F(\tilde{x}_i))) L=N1i=1∑NL(xi,yi)=N1i=1∑NL(xi,G(F(x~i)))
模型和学习
模型
BERT 模型有以下结构。输入是两个合并的单词序列
< cls > , x 1 , x 2 , ⋯ , x m − 1 , < sep > , x m + 1 , x m + 2 , ⋯ , x m + n − 1 , < sep > <\text{cls}>,x_1,x_2,\cdots,x_{m-1},<\text{sep}>,x_{m+1},x_{m+2},\cdots,x_{m+n-1},<\text{sep}> <cls>,x1,x2,⋯,xm−1,<sep>,xm+1,xm+2,⋯,xm+n−1,<sep> 其中, x 1 , x 2 , ⋯ , x m x_1,x_2,\cdots,x_m x1,x2,⋯,xm 是第一个单词序列, x m + 1 , x m + 2 , ⋯ , x m + n − 1 x_{m+1},x_{m+2},\cdots,x_{m+n-1} xm+1,xm+2,⋯,xm+n−1 是第二个单词序列,
H ( 0 ) = X + S + E \bm{H}^{(0)} = \bm{X} + \bm{S} + \bm{E} H(0)=X+S+E 这里,矩阵 S \bm{S} S 是区别前后单词序列的标记序列 S = ( a , a , ⋯ a , b , b , ⋯ b ) \bm{S}=(\bm{a},\bm{a},\cdots\bm{a},\bm{b},\bm{b},\cdots\bm{b}) S=(a,a,⋯a,b,b,⋯b),含有 m + 1 m+1 m+1 个向量 a \bm{a} a 和 n n n 个向量 b \bm{b} b。
使用拼接的单词序列作为输入是让 BERT 不仅能用于以一个文本为输入的任务,如文本分类,也能用于以两个文本为输入的任务,如文本匹配。
之后经过 L L L 个编码层,得到单词表示向量的序列,记作矩阵 H ( L ) \bm{H}^{(L)} H(L):
H ( L ) = transformer_encoder ( H ( 0 ) ) \bm{H}^{(L)} = \text{transformer\_encoder}(\bm{H}^{(0)}) H(L)=transformer_encoder(H(0)) 具体地, H ( L ) = ( h 1 ( L ) , h 2 ( L ) , ⋯ , h m + n ( L ) ) \bm{H}^{(L)} = \left(\bm{h}_1^{(L)},\bm{h}_2^{(L)},\cdots,\bm{h}_{m+n}^{(L)}\right) H(L)=(h1(L),h2(L),⋯,hm+n(L))
其中, h i ( L ) \bm{h}_i^{(L)} hi(L) 是第 i i i 个位置的单词表示向量。BERT 模型中,在每一层,每一个位置的表示向量是该位置的单词基于之前位置和之后位置的上下文的表示。
BERT 模型的输出是在合并的单词序列的各个位置上的条件概率,第 i i i 个位置的单词(包括特殊字符)的条件概率 p i p_i pi 定义为
P θ ( x i ∣ x 1 , x 2 , ⋯ , x i − 1 , x i + 1 , ⋯ , x m + n ) = softmax ( W x ⊤ h i ( L ) ) P_{\bm{\theta}} (x_i|x_1,x_2,\cdots,x_{i-1}, x_{i+1},\cdots,x_{m+n})=\text{softmax}(\bm{W}_x^\top \bm{h}_i^{(L)}) Pθ(xi∣x1,x2,⋯,xi−1,xi+1,⋯,xm+n)=softmax(Wx⊤hi(L)) 其中 W x \bm{W}_x Wx 表示所有单词的权重矩阵。
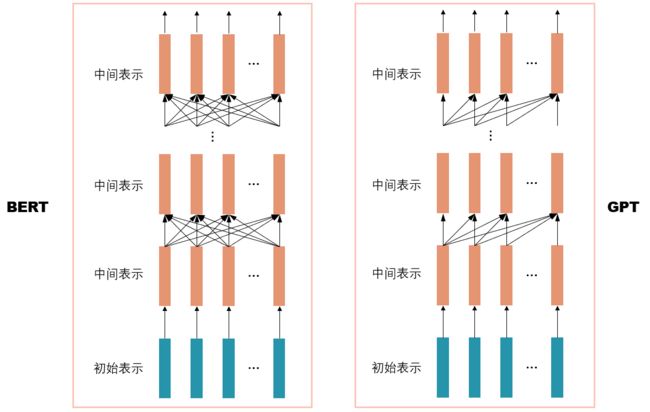
BERT 中编码层的多头自注意力都是双向的,也就是各个位置的单词针对其他位置的单词都进行自注意力计算,这一点与 GPT 不同。下图比较了 GPT 和 BERT 中表示之间关系的差异。BERT 每一层每一个位置的表示都是由下一层所有位置的表示组合而成,而 GPT 中每一层每一个位置的表示都是由下一层之前所有位置的表示组合而成。
预训练
预训练数据的每个样本由两个单词序列 A 和 B 合并组成,中间由特殊字符
BERT 模型的预训练由两部分组成,掩码语言模型化和下句预测。掩码语言模型化的目标是复原输入单词序列中被掩码的单词,可以看作是去噪自编码器学习,对被掩码(噪声)的单词独立地进行复原。下句预测的目标是判断输入单词序列是否来自同一篇文章。
模型特点
BERT 通过其多层多头注意力机制能够有效地表示语言的词汇、语法、语义信息。通过自注意力,每一层的每一个位置的单词表示与其他位置的单词表示组合成新的表示,传递到上一层的同一位置。自注意力是多头的,每个头代表一个侧面,因此每一个位置的单词表示由多个不同侧面的表示组合而成。单词表示的内容可以通过自注意力的权重推测。
BERT 的各层有不同的特点。底层主要表示词汇信息,中层主要表示语法信息,上层主要表示语义信息。
对 BERT 和 GPT 的直观解释是:机器基于大量的语料,做了大量的词语填空(BERT)或词语接龙(GPT)练习,捕捉到了由单词组成句子、再由句子组成文章的各种规律,并且把它们表示并记忆在模型之中。也就是说,BERT 通过无监督学习获取了大量的词汇、语法、语义知识。当用于一个下游任务时,只需要很少的标注数据就可以学习到完成该任务所需的知识。
References
[1] 《机器学习方法》,李航,清华大学出版社。