数据结构---遍历还原二叉树

还原二叉树的原理

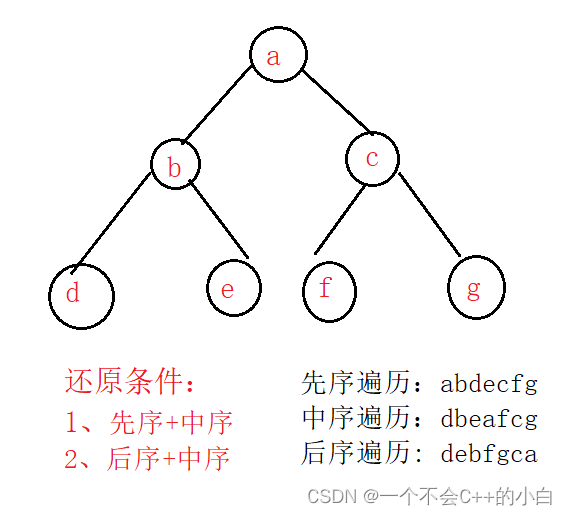
通过遍历的结果来还原二叉树，但要两种遍历结果才能还原一个二叉树，比如：
先序遍历+中序遍历 还原二叉树
后序遍历+中序遍历 还原二叉树
只有这两个模式才能还原，而先序和后序是不可以还原的。

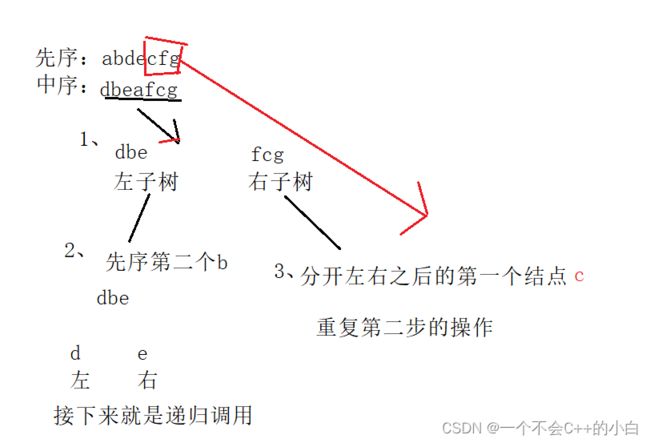
原理：

直接看代码：

//pre和in是两个数组，是用来存放你要输入的先序遍历和中序遍历的结果
//pre[100]= "abdecfg"
//in[100] = "debafcg"
//len是结点个数，也就是数组长度
struct BinTree_node *pre_in_CreateBinTree(char *pre, char *in, int len)
{
	struct BinTree_node *tree;
	if(len == 0)
		return NULL;

	char ch = pre[0];//得到先序遍历的第一个结点
	int index = 0;

	while(in[index] != ch)
		index++;//记录先序遍历的第一个结点在in中寻找，找到下标
	
	tree = (struct BinTree_node *)malloc(sizeof(struct BinTree_node));//开辟结点内存空间
	tree->elem = ch;//数据赋值为先序遍历中的第一个
	tree->ltree = pre_in_CreateBinTree(pre+1, in, index);//递归创建左子树
	tree->rtree = pre_in_CreateBinTree(pre+index+1, in+index+1, len-index-1);//递归创建右子树
//括号里面的参数是缩小范围，只是左子树和右子树的区域
	return tree;
}

中序和后序：

struct BinTree_node *in_post_CreateBinTree(char *in, char *post, int len)
{
	struct BinTree_node *tree;

	if(len == 0)
		return NULL;

	char ch = post[len-1];//后序遍历的最后一个
	int index = 0;
	while(in[index] != ch)
		index++;//在中序中寻找

	tree = (struct BinTree_node *)malloc(sizeof(struct BinTree_node));
	tree->elem = ch;//初始化数据域
	tree->ltree = in_post_CreateBinTree(in, post, index);//创建左子树
	tree->rtree = in_post_CreateBinTree(in+index+1, post+index, len-index-1);//创建右子树

	return tree;
}

总代码

#include 
#include 

struct BinTree_node
{
	unsigned char elem;
	struct BinTree_node *ltree, *rtree;
};

void pre_order(struct BinTree_node *tree);//先序遍历
void in_order(struct BinTree_node *tree);//中序遍历
void pos_order(struct BinTree_node *tree);//后序遍历

struct BinTree_node *create_bintree(void);//创建二叉树，前面讲过
struct BinTree_node *pre_in_CreateBinTree(char *pre, char *in, int len);
struct BinTree_node *in_post_CreateBinTree(char *in, char *post, int len);

int main(void)
{
	struct BinTree_node *mytree;

	char pre[100], in[100], post[100];
	int choose, n;

	printf("1.选择先序和中序:\n");
	printf("2. 选择中序和后序:\n");
	scanf("%d", &choose);

	switch(choose)
	{
		case 1:
			printf("输入结点个数:");
			scanf("%d", &n);
			getchar();
			printf("输入先序遍历的结果:");
			gets(pre);
			printf("输入中序遍历的结果:");
			gets(in);

			mytree = pre_in_CreateBinTree(pre, in, n);
			printf("后序遍历的结果:");
			pos_order(mytree);
			printf("\n");
			break;
		case 2:
			printf("输入结点个数:");
			scanf("%d", &n);
			getchar();
			printf("输入中序遍历的结果:");
			gets(in);
			printf("输入后序遍历的结果:");
			gets(post);

			mytree = in_post_CreateBinTree(in, post, n);
			printf("后序遍历的结果");
			pre_order(mytree);
			printf("\n");
			break;
	}

	return 0;
}

struct BinTree_node *create_bintree(void)
{
	unsigned char flag;
	struct BinTree_node *tree;

	tree = (struct BinTree_node *)malloc(sizeof(struct BinTree_node));
	printf("Please input the node elem:\n");
	while((tree->elem = getchar()) == '\n');
	printf("Do you want to insert l_tree for %c, (Y/N)?\n", tree->elem);
	while((flag = getchar()) == '\n');

	if(flag == 'Y')
		tree->ltree = create_bintree();
	else
		tree->ltree = NULL;

	printf("Do you want to insert r_tree for %c, (Y/N)?\n", tree->elem);
	while((flag = getchar()) == '\n');

	if(flag == 'Y')
		tree->rtree = create_bintree();
	else
		tree->rtree = NULL;

	return tree;
}

void pre_order(struct BinTree_node *tree)
{
	if(tree)
	{
		printf("%c", tree->elem);
		pre_order(tree->ltree);
		pre_order(tree->rtree);
	}
}

void in_order(struct BinTree_node *tree)
{
	if(tree)
	{
		in_order(tree->ltree);
		printf("%c", tree->elem);
		in_order(tree->rtree);
	}
}

void pos_order(struct BinTree_node *tree)
{
	if(tree)
	{
		pos_order(tree->ltree);
		pos_order(tree->rtree);
		printf("%c", tree->elem);
	}
}

struct BinTree_node *pre_in_CreateBinTree(char *pre, char *in, int len)
{
	struct BinTree_node *tree;

	if(len == 0)
		return NULL;

	char ch = pre[0];
	int index = 0;

	while(in[index] != ch)
		index++;
	
	tree = (struct BinTree_node *)malloc(sizeof(struct BinTree_node));
	tree->elem = ch;
	tree->ltree = pre_in_CreateBinTree(pre+1, in, index);
	tree->rtree = pre_in_CreateBinTree(pre+index+1, in+index+1, len-index-1);

	return tree;
}

struct BinTree_node *in_post_CreateBinTree(char *in, char *post, int len)
{
	struct BinTree_node *tree;

	if(len == 0)
		return NULL;

	char ch = post[len-1];
	int index = 0;
	while(in[index] != ch)
		index++;

	tree = (struct BinTree_node *)malloc(sizeof(struct BinTree_node));
	tree->elem = ch;
	tree->ltree = in_post_CreateBinTree(in, post, index);
	tree->rtree = in_post_CreateBinTree(in+index+1, post+index, len-index-1);

	return tree;
}