优先队列——二项队列（binominal queue）

【0】README

0.1） 本文文字描述部分转自 数据结构与算法分析， 旨在理解 优先队列——二项队列（binominal queue） 的基础知识；
0.2） 本文核心的剖析思路均为原创（insert，merge和deleteMin的操作步骤图片示例）， 源代码均为原创；
0.3） for original source code, please visit https://github.com/pacosonTang/dataStructure-algorithmAnalysis/tree/master/chapter6/p152_binominal_queue

---

【1】二项队列相关

1.0）Attention： 二项队列中不允许有高度相同的二项树存在该队列中；
1.1）problem+solution：

• 1.1.1）problem：虽然左式堆和斜堆每次操作花费O（logN）时间， 这有效地支持了合并， 插入和deleteMin， 但还是有改进的余地，因为我们知道， 二叉堆以每次操作花费常数平均时间支持插入。
• 1.1.2）solution： 二项队列支持所有这三种操作（merge + insert + deleteMin）， 每次操作的最坏情形运行时间为O（logN）， 而插入操作平均花费常数时间； （干货——优先队列的三种基本操作——merge + insert + deleteMin）

1.2）相关定义

• 1.2.1） 二项队列定义： 二项队列不同于我们看到的所有优先队列的实现之处在于， 一个二项队列不是一颗堆序的树， 而是堆序树的集合，称为森林；（干货——二项队列的定义和构成，二项队列是二项树的集合，而二项树是一颗堆序树）
• 1.2.2）二项树定义： 堆序树中的每一颗都是有约束的形式。 （干货——二项树的定义）
• 1.2.3）二项树的构成：每一个高度上至多存在一颗二项树， 高度为0的二项树是一颗单节点树； 高度为k 的二项树Bk 通过将一颗二项树 Bk-1 附接到另一颗二项树Bk-1 的根上而构成；（干货——二项树的构成）
  

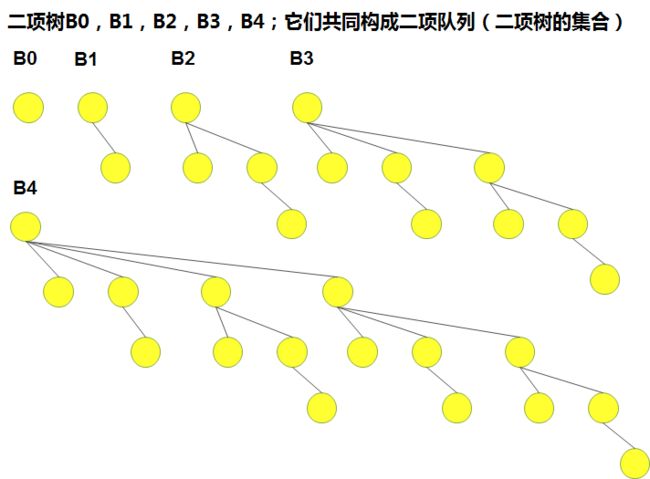
对上图的分析（Analysis）：

• A1）二项树的性质：

  • A1.1）从图中看到， 二项树Bk 由一个带有儿子B0， B1， …, Bk-1的根组成；
  • A1.2）高度为k 的二项树恰好有2^k 个节点；
  • A1.3） 而在深度d 的节点数是 二项系数 。

• A2）如果我们把堆序添加到二项树上， 并允许任意高度上最多有一颗二项树，那么我们能够用二项树的集合唯一地表示任意大小的优先队列；

---

【2】二项队列操作（merge + insert + deleteMin）

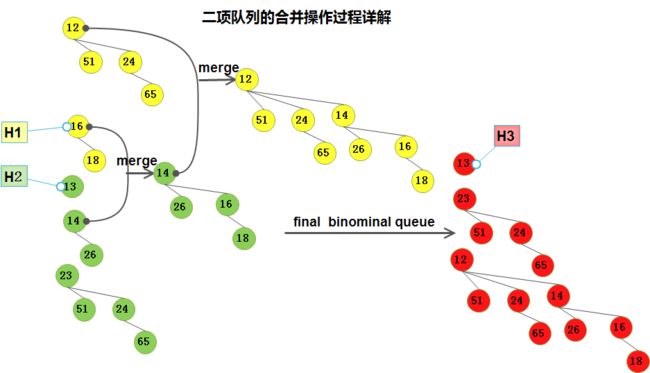
2.1）合并操作（merge） （干货——合并操作的第一步就是查看是否有高度相同的二项树，如果有的话将它们merge）

• step1） H1 没有高度为0的二项树而H2有，所以将H2中高度为0的二项树直接作为H3的一部分；（直接的意思==中间不需要merge）；
• step2） H1 和 H2 中都有高度为1的二项树，将它们进行merge， 得到高度为2的二项树（根为12）；
• step3）现在存在三颗高度为2的二项树（根分别为12， 14， 23），将其中两个进行merge（如merge根为12 和 根为14 的二项树），得到高度为3的二项树；
• step4）所以，最后，我们得到二项队列， 其集合包括：高度为０的二项树（根为13）， 高度为1的二项树（根为23），高度为3的二项树（高度为12）；

Attention）

• A1）显然，merge操作是按照高度升序依次进行的；
• A2）最后得到的二项队列不存在高度相同的二项树，即使存在，也要将高度相同的二项树进行merge；
• A3）二项队里中的二项树的高度不必囊括所有的升序实数，即不必一定是0， 1， 2， 3，4 等等； 也可以是0， 1， 3 等；
• A4）单节点树的高度为0； （干货——树高度从零起跳）
  

2.2）插入操作（insert） （干货——insert操作是merge操作的特例，而merge操作的第一步就是查看是否有高度相同的二项树，如果有的话将它们merge）

• 2.2.1）插入操作实际上： 就是特殊情形的合并， 我们只需要创建一颗单节点树并执行一次merge；
• 2.2.2）更准确地说： 如果元素将要插入的那个优先队列中不存在的最小的二项树是Bi， 那么运行时间与 i + 1 成正比；
  

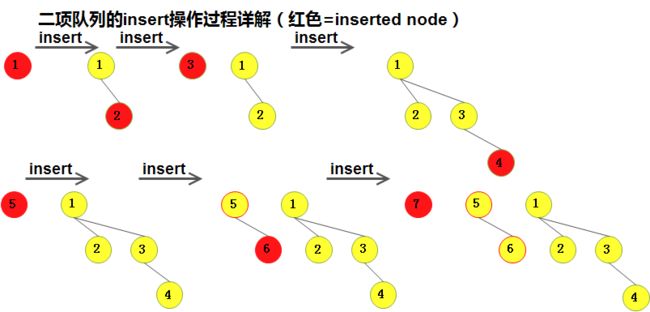
对上图的分析（Analysis）：

• A1） 4 插入之后，与B0（根为3）进行merge， 得到一颗高度为1的树B1’（根为3）；
• A2）将B1’ 与 B1（根为1） 进行merge 得到高度为2 的树B2’（根为1）， 它是新的优先队列；
• A3）在插入7之后的下一次插入又是一个坏情形， 因为需要三次merge操作；

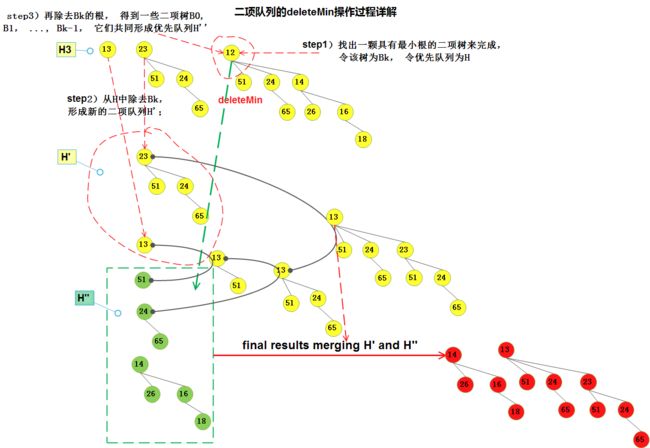
2.3）删除最小值操作（deleteMin）

• step1）找出一颗具有最小根的二项树来完成， 令该树为Bk， 令原始序列为H；
• step2）从H中除去Bk， 形成新的二项队列H’；
• step3）再除去Bk的根， 得到一些二项树B0, B1， …, Bk-1， 它们共同形成优先队列H”；
• step4） 合并H’ 和 H” ， 操作结束；
  

---

【3】 source code and printing results

3.1）source code at a glance
Attention）二项队列的实现源代码用到了 儿子兄弟表示法；

#include "binominal_queue.h" 

#define MINIMAL 10000

int minimal(BinominalQueue bq)
{
    int capacity;
    int i;
    int minimal;
    int miniIndex;  

    minimal = MINIMAL;
    capacity = bq->capacity;
    for(i=0; iif(bq->trees[i] && bq->trees[i]->value < minimal)
        {
            minimal = bq->trees[i]->value;
            miniIndex = i;
        }
    }

    return miniIndex;
}

// initialize the BinominalQueue with given capacity.
BinominalQueue init(int capacity)
{
    BinominalQueue queue;           
    BinominalTree* trees; 
    int i;

    queue = (BinominalQueue)malloc(sizeof(struct BinominalQueue));
    if(!queue)
    {
        Error("failed init, for out of space !");
        return queue;
    }   
    queue->capacity = capacity;

    trees = (BinominalTree*)malloc(capacity * sizeof(BinominalTree));
    if(!trees)
    {
        Error("failed init, for out of space !");
        return NULL;
    }   
    queue->trees = trees;

    for(i=0; iqueue->trees[i] = NULL;
    }

    return queue;
}  

// attention: the root must be the left child of the binominal tree.
int getHeight(BinominalTree root)
{
    int height;     
    if(root == NULL)
    {       
        return 0;       
    }

    height = 1; 
    while(root->nextSibling)
    {
        height++;
        root = root->nextSibling;
    }

    return height;
}


// merge BinominalQueue bq2 into bq1.
void outerMerge(BinominalQueue bq1, BinominalQueue bq2)
{
    int height;
    int i;

    for(i=0; icapacity; i++)
    {
        height = -1;
        if(bq2->trees[i])
        {
            height = getHeight(bq2->trees[i]->leftChild);   
            // attention for the line above
            // height = height(bq2->trees[i]->leftChild); not height = height(bq2->trees[i]);
            merge(bq2->trees[i], height, bq1);
        }                   
    }       
}

// merge tree h1 and h2 = bq->trees[height], 
// who represents the new tree and old one respectively.
BinominalTree merge(BinominalTree h1, int height, BinominalQueue bq)
{           
    if(h1 == NULL)
    {
        return h1;
    }

    if(bq->trees[height] == NULL) // if the queue don't has the B0 tree.
    {       
        bq->trees[height] = h1;
        return bq->trees[height];
    }
    else // otherwise, compare the new tree's height with that of old one.
    {        
        if(h1->value > bq->trees[height]->value) // the new should be treated as the parent of the old.
        {       
            innerMerge(bq->trees[height], height, h1, bq);
        }
        else // the old should be treated as the parent of the new.
        {
            innerMerge(h1, height, bq->trees[height], bq);
        }
    }  

    return h1;
} 

BinominalTree lastChild(BinominalTree root)
{               
    while(root->nextSibling)
    {       
        root = root->nextSibling;
    }

    return root; 
}

// merge tree h1 and h2 = bq->trees[height], 
// who represents the new tree and old one respectively.
BinominalTree innerMerge(BinominalTree h1, int height, BinominalTree h2, BinominalQueue bq)
{
    if(h1->leftChild == NULL)
    {
        h1->leftChild = h2;
    }
    else
    {
        lastChild(h1->leftChild)->nextSibling = h2;
        // attention for the line above
        // lastChild(h1->leftChild)->nextSibling = h2 not lastChild(h1)->nextSibling = h2
    }
    height++;
    bq->trees[height-1] = NULL;
    merge(h1, height, bq);  

    return h1;
} 

// insert an element with value into the priority queue.
void insert(ElementType value, BinominalQueue bq)
{
    TreeNode node;

    node = (TreeNode)malloc(sizeof(struct TreeNode));
    if(!node)
    {
        Error("failed inserting, for out of space !");
        return ;
    }
    node->leftChild= NULL;
    node->nextSibling = NULL;   
    node->value = value;    

    merge(node, 0, bq);         
}

// analog print node values in the binominal tree, which involves preorder traversal. 
void printPreorderChildSibling(int depth, BinominalTree root)
{           
    int i;

    if(root) {      
        for(i = 0; i < depth; i++)
            printf("    ");
        printf("%d\n", root->value);            
        printPreorderChildSibling(depth + 1, root->leftChild);                                  
        printPreorderChildSibling(depth, root->nextSibling);
    } 
    else
    {
        for(i = 0; i < depth; i++)
            printf("    ");
        printf("NULL\n");
    }
}

// print Binominal Queue bq
void printBinominalQueue(BinominalQueue bq)
{
    int i;

    for(i=0; icapacity; i++)
    {
        printf("bq[%d] = \n", i);
        printPreorderChildSibling(1, bq->trees[i]);
    }   
}

void deleteMin(BinominalQueue bq)
{
    int i;  
    BinominalTree minitree; 
    BinominalTree sibling;

    i = minimal(bq);
    minitree = bq->trees[i]->leftChild; //minitree->value=51
    free(bq->trees[i]);
    bq->trees[i] = NULL;            

    while(minitree)
    {
        sibling = minitree->nextSibling;
        minitree->nextSibling = NULL;
        merge(minitree, getHeight(minitree->leftChild), bq);        
        minitree = sibling;
    }       
}

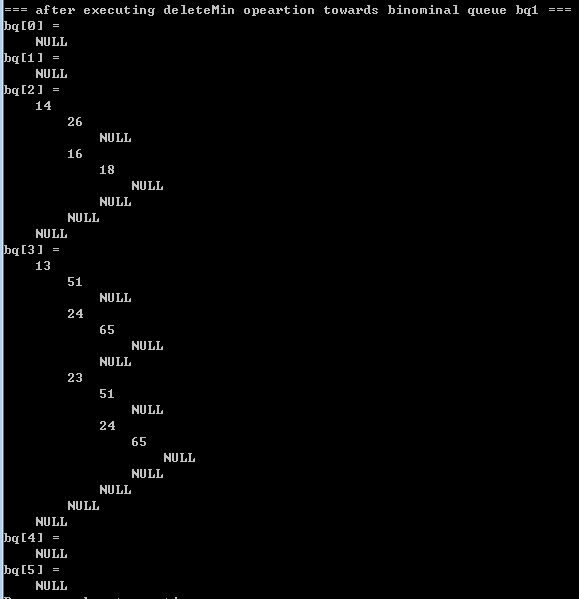
3.2） printing results
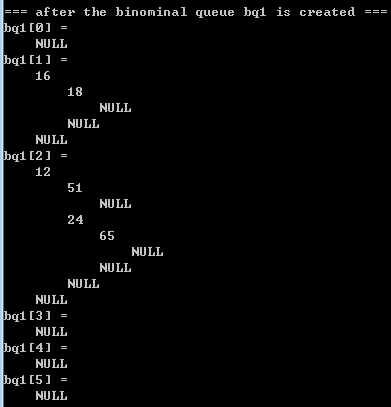
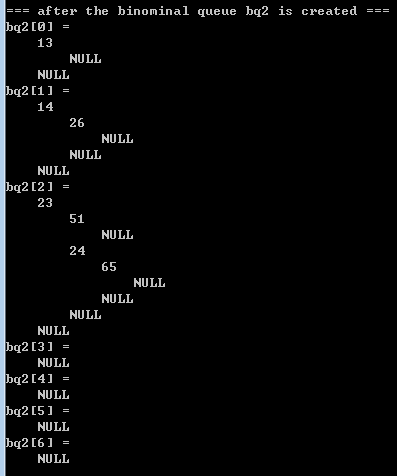
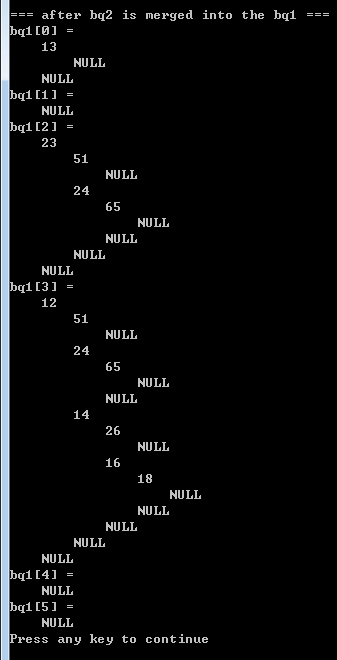
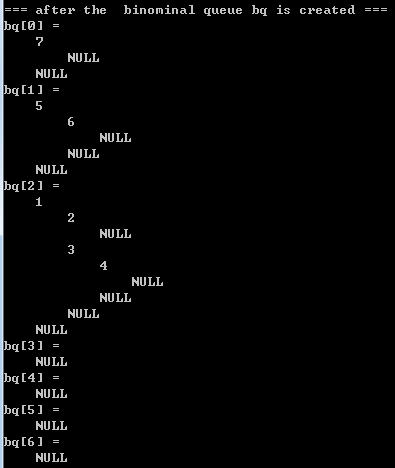