队列实现栈 \ 栈实现队列 \ 循环队列

 本文是写在上一篇文章的基础之上的，如果你还不清楚栈和队列如何实现，请先移步上一篇文章。

目录

一、用两个队列实现栈

1、题目描述

2、解题思路

3、代码实现

1）结构定义及初始化

 2）插入

3)删除

4）取栈顶元素

5）判空与销毁

二、用两个栈实现队列

1、题目描述

2、解题思路

3、代码实现

1）结构定义及初始化

2）插入 

3) 开头元素

4）删除 

5）判空 

6) 销毁 

三、循环队列

1、题目描述

2、解题思路 

1）用链表实现

2）用数组实现

3、代码实现

1)结构构造及初始化

2）判满和判空

3）插入

4) 删除

5)取头

6）取尾

7）销毁

---

一、用两个队列实现栈

1、题目描述

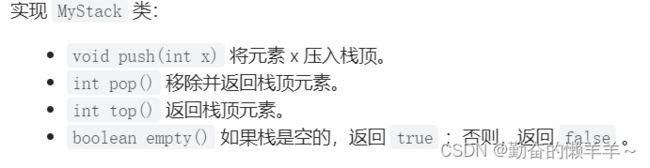
请你仅使用两个队列实现一个后入先出（LIFO）的栈，并支持普通栈的全部四种操作（push、top、pop 和 empty）。

typedef struct {

} MyStack;


MyStack* myStackCreate() {

}

void myStackPush(MyStack* obj, int x) {

}

int myStackPop(MyStack* obj) {

}

int myStackTop(MyStack* obj) {

}

bool myStackEmpty(MyStack* obj) {

}

void myStackFree(MyStack* obj) {

}

2、解题思路

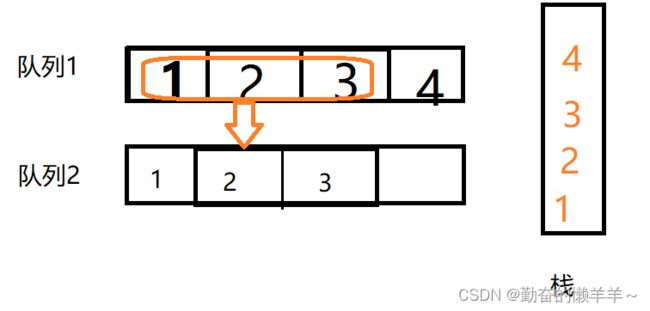
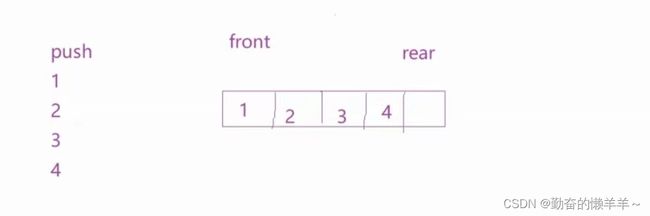
如图，如果我们想删除栈顶元素4，在两个对列中如何实现呢？

显然，我们可以让队列1中的前3个元素都移到队列2中，这时，4就可以出来了

此时，如果我们想再插入数据，则应往队列2插入，即非空的队列

如果想再删除，就再重复上述步骤，把要删除的数据前的数据导入空队列即可。 

3、代码实现

1）结构定义及初始化

typedef struct {
    Queue q1;
    Queue q2;
} MyStack;

为什么下面要malloc而不是直接MyStack obj；

因为MyStack obj；obj是局部变量，出作用域就直接销毁了

MyStack* myStackCreate() {
    MyStack* obj = (MyStack*) malloc( sizeof (MyStack) );
    if(obj==NULL)
    {
        perror("malloc failed");
        return NULL;
    }
    QueueInit(&obj->q1);//初始化两个队列
    QueueInit(&obj->q2);
    return obj;
}

 2）插入

往不是空的队列插入。

void myStackPush(MyStack* obj, int x) {
    if(!QueueEmpty(&obj->q1))
    {
        QueuePush(&obj->q1,x);
    }
    else
    {
        QueuePush(&obj->q2,x);
    }
}

3)删除

将不是空的队列的元素一个个导入空队列（除最后一个），并删除。

int myStackPop(MyStack* obj) {
    Queue* pEmpty = &obj->q1;
    Queue* pNoEmpty = &obj->q2;
    if(!QueueEmpty(&obj->q1))
    {
        pEmpty=&obj->q2;
        pNoEmpty=&obj->q1;
    }

    while(QueueSize(pNoEmpty)>1)
    {
        QueuePush(pEmpty,QueueFront(pNoEmpty));
        QueuePop(pNoEmpty);
    }
    int top=QueueFront(pNoEmpty);
    QueuePop(pNoEmpty);
    return top;
}

4）取栈顶元素

int myStackTop(MyStack* obj) {
    if(!QueueEmpty(&obj->q1))
    {
        return QueueBack(&obj->q1);
    }
    else
    {
        return QueueBack(&obj->q2);
    }
}

5）判空与销毁

bool myStackEmpty(MyStack* obj) {
    return QueueEmpty(&obj->q1) && QueueEmpty(&obj->q2);
}

void myStackFree(MyStack* obj) {
    QueueDestroy(&obj->q1);
    QueueDestroy(&obj->q2);
    free(obj);
}

二、用两个栈实现队列

1、题目描述

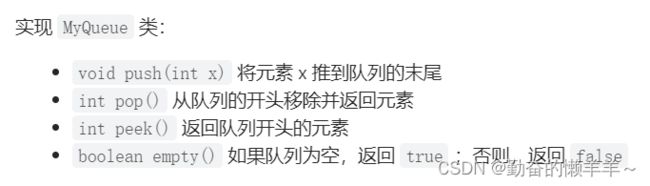
请你仅使用两个栈实现先入先出队列。队列应当支持一般队列支持的所有操作（push、pop、peek、empty）

typedef struct {

} MyQueue;


MyQueue* myQueueCreate() {

}

void myQueuePush(MyQueue* obj, int x) {

}

int myQueuePop(MyQueue* obj) {

}

int myQueuePeek(MyQueue* obj) {

}

bool myQueueEmpty(MyQueue* obj) {

}

void myQueueFree(MyQueue* obj) {

}

2、解题思路

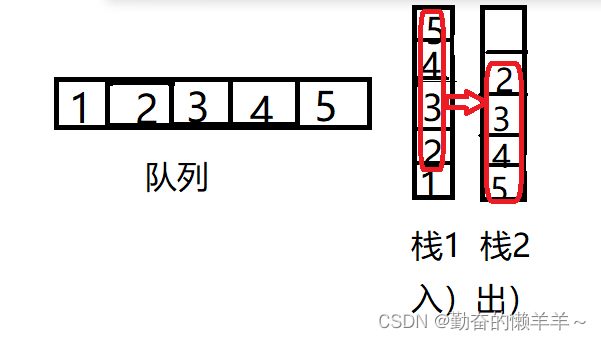
栈1负责数据的插入，栈2负责数据的删除。

如图，要想删除数据1，就应该让栈1中1上面的数据都到栈2去，再把栈1中的数据1删除。

此时，如果我们想继续删除数据2，就可以在栈2中直接删除。

如果我们想插入数据，就在栈1插入即可，需要注意的是，只有当栈2为空时，才可把栈1数据导入，否则将会让顺序打乱。

3、代码实现

1）结构定义及初始化

typedef struct {
    ST pushst;
    ST popst;
} MyQueue;

MyQueue* myQueueCreate() {
    MyQueue*pst=(MyQueue*)malloc(sizeof(MyQueue));
    if(pst==NULL)
    {
        perror("malloc failed");
        return NULL;
    }
    STInit(&pst->pushst);
    STInit(&pst->popst);
    return pst;
}

2）插入 

void myQueuePush(MyQueue* obj, int x) {
    STPush(&obj->pushst,x);   
}

3) 开头元素

int myQueuePeek(MyQueue* obj) {
    if(STEmpty(&obj->popst))
    {
        while(!STEmpty(&obj->pushst))
        {
            STPush(&obj->popst,STTop(&obj->pushst));
            STPop(&obj->pushst);
        }
    }
    int front=STTop(&obj->popst);
    return front;
}

---

4）删除 

int myQueuePop(MyQueue* obj) {
    int top=myQueuePeek(obj);
    STPop(&obj->popst);
    return top;
}

5）判空 

bool myQueueEmpty(MyQueue* obj) {
    return STEmpty(&obj->pushst) && STEmpty(&obj->popst);
}

6) 销毁 

void myQueueFree(MyQueue* obj) {
    STDestroy(&obj->popst);
    STDestroy(&obj->pushst);
    free(obj);
}

三、循环队列

1、题目描述

设计你的循环队列实现。 循环队列是一种线性数据结构，其操作表现基于 FIFO（先进先出）原则并且队尾被连接在队首之后以形成一个循环。它也被称为“环形缓冲器”。

循环队列的一个好处是我们可以利用这个队列之前用过的空间。在一个普通队列里，一旦一个队列满了，我们就不能插入下一个元素，即使在队列前面仍有空间。但是使用循环队列，我们能使用这些空间去存储新的值。

typedef struct {

} MyCircularQueue;


MyCircularQueue* myCircularQueueCreate(int k) {

}

bool myCircularQueueEnQueue(MyCircularQueue* obj, int value) {

}

bool myCircularQueueDeQueue(MyCircularQueue* obj) {

}

int myCircularQueueFront(MyCircularQueue* obj) {

}

int myCircularQueueRear(MyCircularQueue* obj) {

}

bool myCircularQueueIsEmpty(MyCircularQueue* obj) {

}

bool myCircularQueueIsFull(MyCircularQueue* obj) {

}

void myCircularQueueFree(MyCircularQueue* obj) {

}

2、解题思路 

1）用链表实现

多开一个结点，当front==rear时，为空。

当front==rear->next时，为满。

 但是，用链表取尾其实不好取。

2）用数组实现

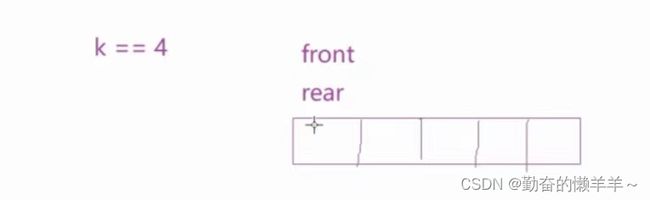
用数组实现也跟用链表类似，要多开一个空间。（k==4时，就要开5个空间。）

当front=rear时，为空。 

当rear到k+1时，要模一下k+1。 

 当rear+1=front时，为满。

3、代码实现

1)结构构造及初始化

typedef struct {
    int* a;
    int front;
    int rear;
    int k;
} MyCircularQueue;

MyCircularQueue* myCircularQueueCreate(int k) {
    MyCircularQueue* obj = (MyCircularQueue*)malloc(sizeof(MyCircularQueue));
    obj->front = obj->rear=0;
    obj->a = (int* )malloc(sizeof(int)*k);
    obj->k = k;
    return obj;
}

2）判满和判空

需要注意的是，当rear在k+1的位置时，它的下一个位置就超出数组范围了，所以应该让rear+1模k+1

bool myCircularQueueIsEmpty(MyCircularQueue* obj) {
    return obj->rear==obj->front;
}


bool myCircularQueueIsFull(MyCircularQueue* obj) {
    return (obj->rear+1)%(obj->k+1)==obj->front;
}

3）插入

插入前应该先判断数组有没有满

同时，rear也应该模k+1

bool myCircularQueueEnQueue(MyCircularQueue* obj, int value) {
    if(myCircularQueueIsFull(obj))
        return false;
    obj->a[obj->rear++]=value;
    obj->rear%=(obj->k+1);


    return true;
}

4) 删除

bool myCircularQueueDeQueue(MyCircularQueue* obj) {
    if(myCircularQueueIsEmpty(obj))
        return false;


    obj->front++;
    obj->front%=(obj->k+1);


    return true;
}

5)取头

int myCircularQueueFront(MyCircularQueue* obj) {
    if(myCircularQueueIsEmpty(obj))
        return -1;
    return obj->a[obj->front];

}

6）取尾

需要注意的是，当rear为0时，rear减1就变成-1了，会越界，所以应该：

(obj->rear-1+obj->k+1) % (obj->k+1)

int myCircularQueueRear(MyCircularQueue* obj) {
    if(myCircularQueueIsEmpty(obj))
        return -1;
    return obj->a[(obj->rear-1+obj->k+1) % (obj->k+1)];
}

7）销毁

void myCircularQueueFree(MyCircularQueue* obj) {
    free(obj->a);
    free(obj);
}