数据结构 - 堆与堆排序

一、介绍

所谓排序，就是指按照一定的算法将一些同类型、无序的数据转换成有序的数据，例如将【1,4，3】转换成【1，3，4】。实现这种要求的算法数不胜数，今天介绍的是其中一个：堆排序。

所谓堆排序，就是通过使用一种叫堆的数据结构实现上述的排序算法，堆排序是选择排序的一种。

二、选择排序

选择排序是对一系列基本思想相同的排序算法的统称，选择排序包含了简单选择排序、堆排序。

思想：对于一组具有n个元素的集合L，需要对其进行n趟遍历，每一趟遍历（如第i趟）都在当前位置后面的n-i+1个元素中选择一个关键字最小的元素，作为有序集合的第i个元素，直到第n-1趟遍历完成，原序列中只剩下一个元素为止，就不用再选了，因为它肯定是有序集合中最大的元素。

三、堆的定义

定义：对于一个具有n个元素的集合L，如果满足以下条件其中一个，那么该集合就称为堆：

1. 第i个元素>=第i+1个元素，且第i个元素>=第i+2个元素。
2. 第i个元素<=第i+1个元素，且第i个元素<=第i+2个元素。

如果满足第1个条件，则该堆可称为大根堆。相反，如果满足第二个条件，则称为小根堆。

因为该定义是根据元素在序列的位置判定的，那么我们可以很直观的想到通过数组来保存这个序列。但因为数组中元素的位置是从0开始的，那么上述定义就无法满足，因此我们需要对其进行修改。

定义：对于一个具有n个元素的数组L，如果满足以下条件其中一个，那么该数组就称为堆：

1. L[i] >= L[2i+1]，且L[i] >= L[2i+2]。
2. L[i] <= L[2i+1]，且L[i] <= L[2i+2]。

如果满足第1个条件，则该堆可称为大根堆。相反，如果满足第二个条件，则称为小根堆。

从修改后的定义来看，堆的物理结构可以用数组表示，而逻辑结构其实就是一颗完全二叉树。

那么我们可以根据其逻辑结构重新定义：

定义：对于一棵完全二叉树，如果满足以下条件其中一个，那么该完全二叉树就称为堆：

1. 某个节点的关键字 > 该节点的左孩子节点的关键字，且该节点的关键字 > 该节点的右孩子节点的关键字
2. 某个节点的关键字 < 该节点的左孩子节点的关键字，且该节点的关键字 < 该节点的右孩子节点的关键字

如果满足第1个条件，则该堆可称为大根堆。相反，如果满足第二个条件，则称为小根堆。

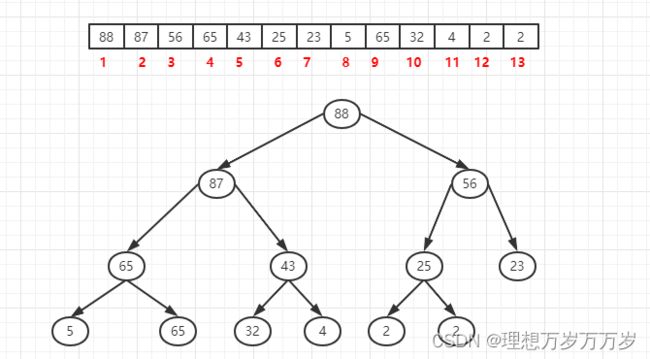
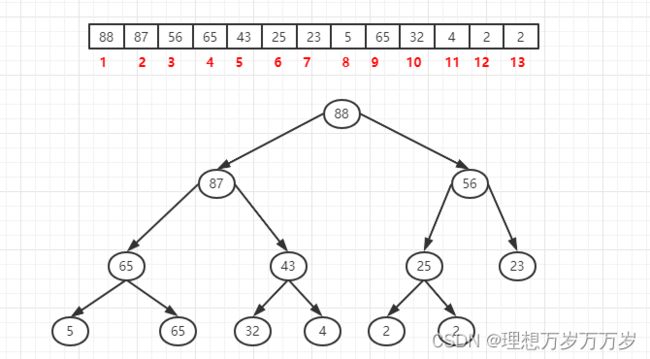
通过图示更清晰直观的理解堆的定义，以大根堆为例

从以上描述以及图片示例，很显然显然，根可以保证根元素为集合中最大值或最小值，但整体来看根不是一个有序集合

四、堆排序思想

将一组具有n个元素的序列L初始化为堆，输出堆顶元素，此时获取的一定是该数组中关键字最大的元素，将原数组中最后一个元素移动至堆顶，此时堆结构被破坏，需要将被破坏的堆结构再一次堆化。再次输出堆顶元素，以此类推，直到堆结构中的所有元素都被输出。不难发现，输出的元素构成一个有序序列。

堆排序中需要解决两个问题：

• 如何将无序的序列初始化为堆
• 堆顶元素输出后，如何将剩余的元素重新堆化

五、将序列堆化

将一个元素序列进行堆化是堆排序的关键。

以大根堆为例，对于一个具有n个结点的完全二叉树，最后一个节点是第 $\lfloor n/2\rfloor$个节点的孩子节点(完全二叉树的概念)，对第 $\lfloor n/2\rfloor$ 个节点为根的子树进行调整，如果根节点的关键字小于 左右孩子节点关键字的较大者，则与关键字较大的节点进行交换，使该子树成为大顶堆。依次向前面的第$\lfloor n/2\rfloor -1$ 个节点至第1个节点重复上述操作，但是其中可能会使已经满足大顶堆的孙子子树被破坏，于是继续采用上述方法重新构造孙子子树的堆，直到根节点。

如下图所示，将具有13个元素的序列进行堆化。

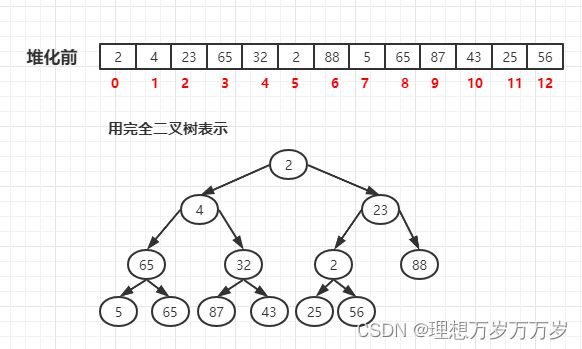
1. 该序列最初结构如下

   

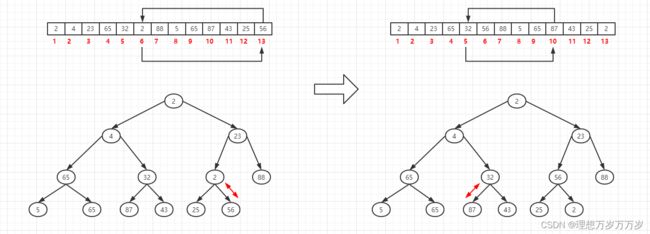
2. 第$\lfloor 13/2\rfloor =6$个元素为根的子树中，因为2<56，所以将第6个元素与第13个元素位置互换。第5个元素为根的子树中，因为32<87，所以将第5个元素与第10个元素位置互换

   

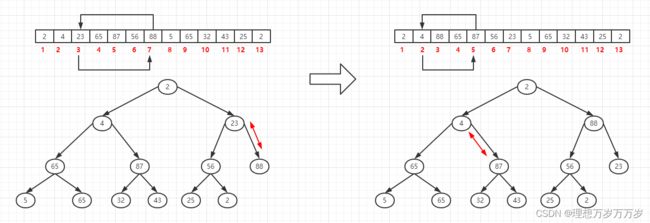
3. 第4个元素为根的子树中，根节点关键字最大，因此该子树本身就是一个大顶堆，无需任何操作。第3个元素为根的子树中，因为23<88，所以将第3个元素与第7个元素位置互换。第2个元素为根的子树中，因为4<87，所以将第2个元素与第5个元素位置互换。

   

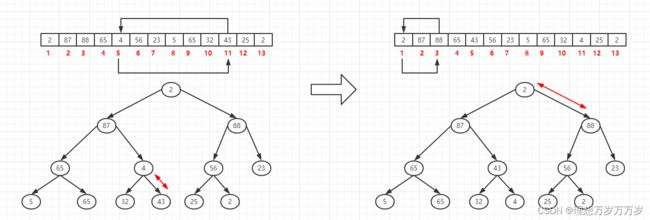
4. 当第2个元素与第5个元素互换位置后，以第5个元素为根的子树的堆结构被破坏，因此需要重新调整以第5个元素为根的子树，第5个元素为根的子树中，因为4<43，所以将第5个元素与第11个元素位置互换，至此，以第2个元素为根的整个子树即满足大顶堆。再来看第1个元素，因为2<88，所以将第1个元素与第3个元素位置互换。

   

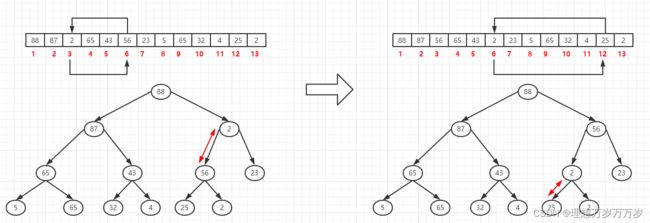
5. 将第1个元素与第3个元素位置互换后，以第3个元素为根的子树的堆结构被破坏，需要重新调整，因为2<56，所以将第3个元素与第6个元素位置互换。互换完成后，以第6个元素为根的子树的堆结构又被破坏，需要重新调整，因为2<25，所以将第6个元素与第12个元素位置互换。

   

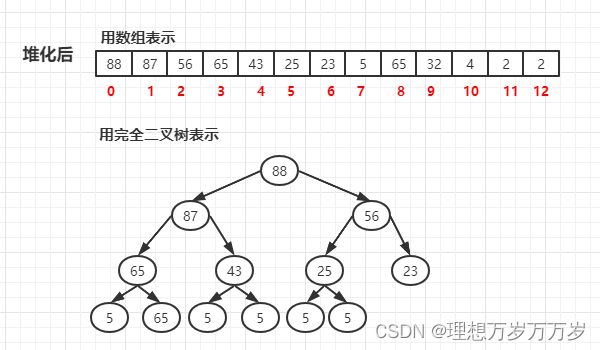
6. 最后得到的结果如下图所示

   

堆化的Java代码实现如下：

public static void heapify(int[] array) {
    // 最大下标
    int maxIndex = array.length - 1;

    // i向上遍历
    for (int rootIndex=(maxIndex-1)/2; rootIndex>=0; rootIndex--) {
        // j向下遍历
        for (int j=rootIndex*2+1; j<=maxIndex; j=j*2+1) {
            int x = array[rootIndex];
            if (j + 1 <= maxIndex && array[j] < array[j+1]) {
                // 如果右节点<根节点，则j++，将j移动至左节点
                // 也就是说，将j移动至较大的子节点
                j++;
            }
            if (array[j] <= x) {
                // 符合大顶堆
                break;
            } else {
                // 不符合，则进行交换
                array[rootIndex] = array[j];
                array[j] = x;
                rootIndex = j;
            }
        }
    }
}

输入：

堆化：

由此可见，堆结构中的元素序列是无序的，但该序列的第一个元素始终都是最大值

六、排序

利用堆结构对排序进行排序的算法逻辑大致如下：

将堆化后的序列中的堆顶元素与第n个元素位置互换，此时序列的最后一个元素为最大值。剩余的n-1个元素不符合堆结构，因此将剩下的n-1个元素重新堆化，堆顶元素为该n-1个元素中的最大值，将堆顶元素与第n-1个元素位置互换，此时序列的最后两个元素为该序列的最大值，且这最后两个元素为递增序列。以此类推，直到该序列中只剩下一个元素，即为最小值，直接作为序列的第一个元素即可。

回过头来看，这个算法逻辑与选择排序的基本思想完全相同。

下面来看一下算法实现：

public static void sort(int[] array) {
    // 先将该序列进行堆化处理
    heapify(array);

    // 堆顶元素与最后一个元素位置互换，并对剩余元素堆化处理
    for (int i = 0; i < array.length; i++) {

        // 位置互换，第0个元素与第array.length-1个元素互换，第1个元素与第array.length-2个元素互换
        int x = array[array.length-1 - i];
        array[array.length-1 - i] = array[0];
        array[0] = x;

        //将剩余元素堆化
        heapify(array, array.length-2 - i);
    }
}

大家应该很容易注意到，有两个堆化方法heapify，因为在前面我们已经写好了对一个完整的序列进行堆化的方法，但它只能对完整的序列进行堆化，无法堆化其子序列(即剩余元素)，因此我对heapify(int[] array)方法进行重载为heapify(int[] array, int index)

/**
 * 堆化
 * @param array 序列
 * @param index 对index元素前的元素进行堆化
 */
public static void heapify(int[] array, int index) {
    // i向上遍历
    for (int rootIndex = (index -1)/2; rootIndex>=0; rootIndex--) {
        // j向下遍历
        for (int j = rootIndex*2+1; j<= index; j=j*2+1) {
            int x = array[rootIndex];
            if (j + 1 <= index && array[j] < array[j+1]) {
                // 如果右节点<根节点，则j++，将j移动至左节点
                // 也就是说，将j移动至较大的子节点
                j++;
            }
            if (array[j] <= x) {
                // 符合大顶堆
                break;
            } else {
                // 不符合，则进行交换
                array[rootIndex] = array[j];
                array[j] = x;
                rootIndex = j;
            }
        }
    }
}

因为heapify(int[] array)和heapify(int[] array, int index)这两个重载方法逻辑完全一致，因此对heapify(int[] array)再稍作修改，使其调用heapify(int[] array, int index)方法，增加代码的复用性。

public static void heapify(int[] array) {
    // 最大下标
    int maxIndex = array.length - 1;

    heapify(array, maxIndex);
}

下面我们对其进行测试：

七、向堆中插入元素

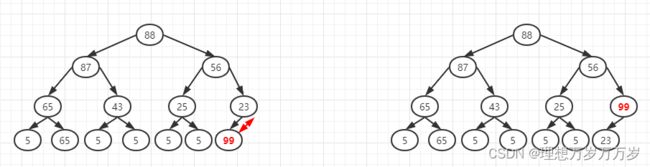
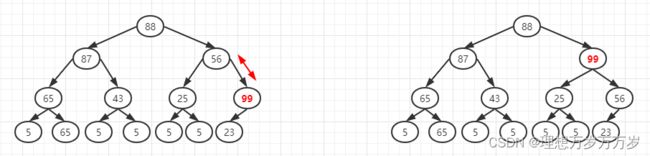
堆结构支持插入操作，将要插入的元素放在序列的末尾，或者说将该元素放在堆的末尾，然后对该元素按照前面堆化的方法进行向上调整，直到满足堆结构。

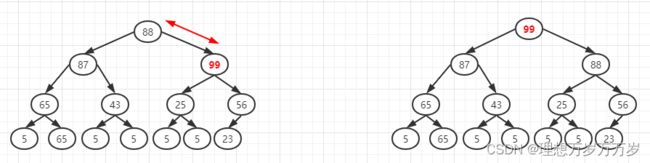
在下图中的大顶堆中插入元素90

1. 将元素90放在大顶堆的尾部，因为99>23，所以将新节点99与其父节点交换位置

   

2. 因为99>56，所以将该节点与其父节点交换位置

   

3. 继续向上调整

   

最后就得到一个插入节点后的大顶堆。

八、性能分析

空间效率

在堆化的过程中需要元素交换时，我们借助一个临时变量完成，在排序中输出堆顶元素时借助一个临时变量进行元素交换，总之我们是借助了常数个临时变量进行元素替换，因此空间复杂度为O(1)。

时间效率

堆化的时间复杂度为O(n),之后有n-1次向下调整操作，每次调整的时间复杂度为O(h)，因此在最好、平均、最坏的情况下，堆排序的时间复杂度为$O(nlo{g}_{2}n)$。

稳定性

所谓稳定性，指的就是在排序前后，序列中相同元素的相对位置是否发生变化，如果有变化，则不是稳定的，否则是稳定的。

堆排序不是一个稳定的排序算法，因为在调整时，有可能把后面相同的元素调整到前面。例如，对于序列{1, 2, 2}，最终排序的结构有可能是{1, 2, 2}，

九、应用

• 在Java集合中，堆应用于优先级队列PriorityQueue，该类通过使用比较器对集合中的元素进行关键字段比较，最终得到一个按照优先级实现的堆结构。
• 在1亿个数中选出前100个最大值，首先将该1亿个数中的前100个调整为小顶堆，再从第101个元素开始遍历剩余的数，如果比堆顶元素大，则替换堆顶元素再堆化，若小于堆顶元素则舍弃，待数据读取完毕，堆中的100个数即为所求。

在我们的人生中，成功只是一时的，失败才是主旋律，这个世上只有一种真正的英雄主义，那就是认清生活的真相，并且仍然热爱它，