基于机器学习算法对电动汽车能耗估计

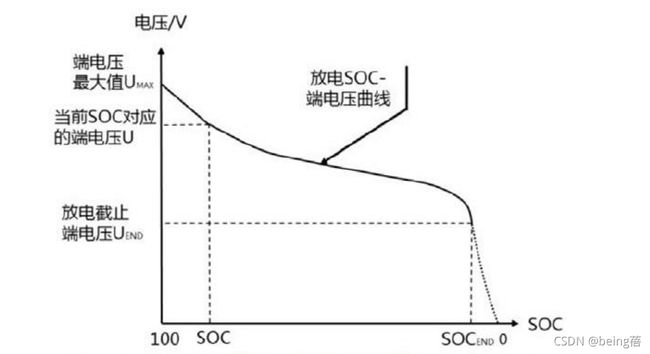
1.车辆剩余续驶里程的定义

  定义：电动汽车行驶过程中，从电池当前状态当完全放电状态，车辆能够行驶的距离。车辆剩余续驶里程主要由剩余可用能量和汽车未来能耗两个因素决定。在前面的研究中，我们可用利用安培积分法、速度对时间积分、KNN回归预测等方法准确预测出SOC，结合电压就可以估算出电池可用能量。车辆自身质量、结构及其零件的性能、电机效率、电池内阻消耗、胎压、造型这些因素都会对车辆的行驶阻力造成影响，继而影响车辆的行驶能耗。另外不同的驾驶员对车辆内部的需求不同，其中空调的使用对电动汽车的能耗有着较为明显的影响。
  我们很难根据现有的数据预测出汽车的能耗，因此采用基于过去一段时间的平均能耗估计未来行驶的平均能耗的方法来计算电动汽车的平均能耗。

2.电动汽车平均能耗的计算方法

2.1电池可用能量的定义

  利用SOC与放电电压曲线围成的面积来表示电池的可用能量。

2.2SOC与电压的线性表达式

  从前面的研究可以知道，在车辆行驶状态下总电压和SOC之间相关性能够达到0.96以上，建立线性模型，求解出权重w和偏执b。

with open(csv_name) as csvfile:
    csv_data = pd.read_csv(csvfile)  # header=1默然不读取表头
    csv_data.dropna(inplace=True)  # 删除SOC为缺失值的行
    csv_data.reset_index(drop=True, inplace=True)
ls = []
for i in range(csv_data.shape[0]):
    # 防止出现噪点
    if csv_data['充电状态'][i] == 3 and csv_data['累计里程'][i] != None and csv_data['总电压'][i] >= 500:
        ls.append(i)

# 划分数据集
x_train, x_test, y_train, y_test = train_test_split(csv_data.iloc[ls, 6:7], csv_data.iloc[ls, 9:10],
                                                    train_size=0.95, random_state=6)

lineModel = LinearRegression()
lineModel.fit(x_test, y_test)
a1 = lineModel.coef_[0][0]
b = lineModel.intercept_[0]
print("SoC=%.4f*S%.4f" % (a1, b))
print("得分", lineModel.score(x_train, y_train))
plt.scatter(x_train, y_train)
plt.plot(x_train, lineModel.predict(x_train), c='red')
plt.xlabel('U')
plt.ylabel('SOC')
plt.show()

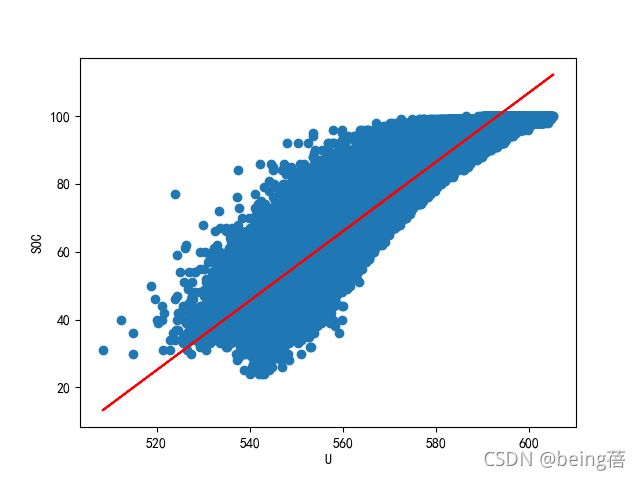
  计算得出w=1.0233、b=-507.0399，测试集评分为0.8913，因此只需要根据电动汽车两种状态下的总电压就可以估算出电池的SOC，进而求出电池所消耗的能量。

2.3电动汽车平均功耗定义

  根据公式P=E/S就能够定义出电动汽车的平均功耗。

ls = []
ls_son = []
for i in range(csv_data.shape[0]):
    if csv_data['充电状态'][i] == 3 and csv_data['累计里程'][i] != None:
        ls_son.append(i)
    elif csv_data['充电状态'][i] == 1:
        if len(ls_son) > 100:
            ls.append(ls_son)
        ls_son = []

res_ls = []
w = 1.0233
b = -507.0399
for index in ls:
    data = csv_data.iloc[index, :]
    # 积分法
    # ans = trapz(data['总电压'].tolist(), data['SOC'].tolist(), dx=0.001) / (
    #             data['累计里程'].tolist()[-1] - data['累计里程'].tolist()[0])
    # 求解围成的面积
    s = (data['总电压'].tolist()[-1] - data['总电压'].tolist()[0]) * ((w * data['总电压'].tolist()[-1] - b)
                                                                - (w * data['总电压'].tolist()[0] - b)) / 2

    res_ls.append(abs(s))

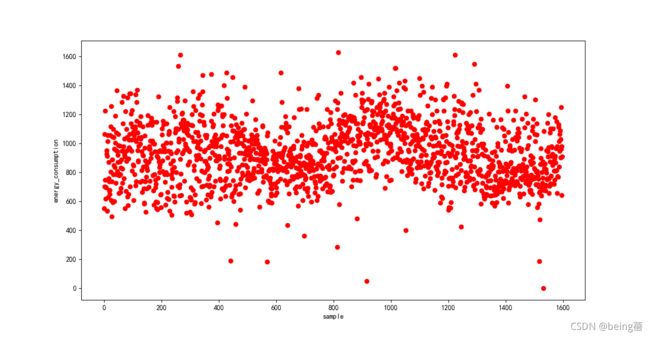
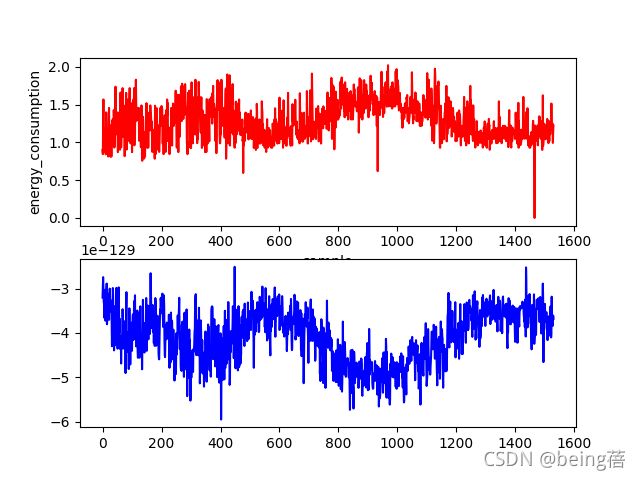
plt.scatter(range(len(res_ls)), res_ls, c='r')
plt.xlabel('sample')
plt.ylabel('energy_consumption')
plt.show()

  采用积分法结果如下所示

3.方法改进

3.1续驶里程估计

  直接利用SOC代表电池的可用能量，根据公式s=(soc1-soc2)/p就可用计算出电动汽车的续驶里程。

csv_name = 'C:\\Users\\刘志军\Desktop\\科研\\2021数字汽车大赛创新组赛题数据Part2\\vin2=LVCB4L4D0HM002829\\part-00367-741da358-7624-4bb4-806b-835c106c6b2d.c000.csv'
with open(csv_name) as csvfile:
    csv_data = pd.read_csv(csvfile)  # header=1默然不读取表头
    csv_data.dropna(inplace=True, subset=['SOC', '总电压'])  # 删除SOC为缺失值的行
    csv_data.reset_index(drop=True, inplace=True)
ls = []
ls_son = []
for i in range(csv_data.shape[0]):
    if csv_data['充电状态'][i] == 3 and csv_data['累计里程'][i] != None:
        if np.isnan(csv_data['累计里程'][i]):
            continue
        ls_son.append(i)
    elif csv_data['充电状态'][i] == 1:
        if len(ls_son) > 300:
            ls.append(ls_son)
        ls_son = []
res_ls = []
for index in ls:
    data = csv_data.iloc[index, :]
    ans =(data['SOC'].tolist()[0]-data['SOC'].tolist()[-1])/(data['累计里程'].tolist()[-1] - data['累计里程'].tolist()[0])
    res_ls.append(abs(ans))
print(np.mean(res_ls))
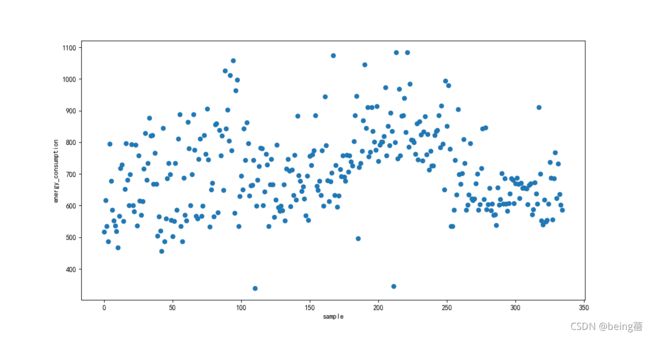
plt.plot(range(len(res_ls)), res_ls, c='r')
plt.xlabel('sample')
plt.ylabel('energy_consumption')
plt.show()

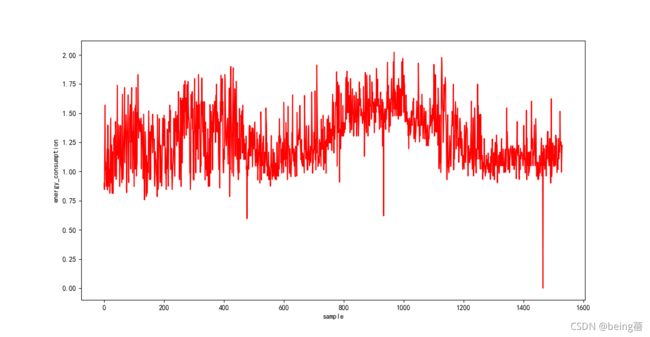
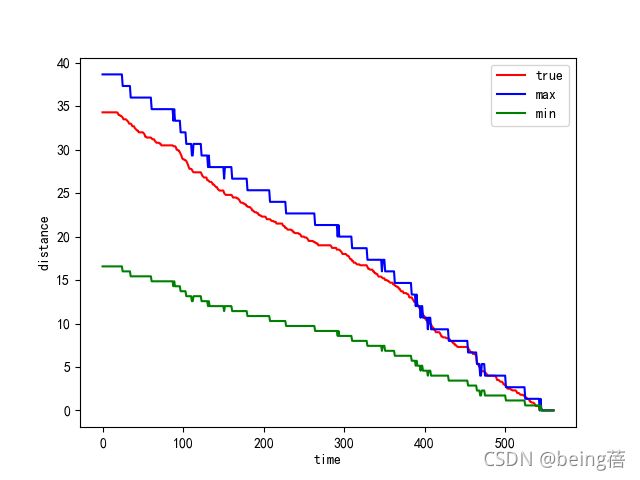
  可以很容易看出，电动汽车的一个平均功耗在0.75到1.75之间，将平均功耗代入计算公式中，可以估计续驶里程的范围。

csv_name = 'C:\\Users\\刘志军\Desktop\\科研\\2021数字汽车大赛创新组赛题数据Part2\\vin2=LVCB4L4D0HM002829\\part-00367-741da358-7624-4bb4-806b-835c106c6b2d.c000.csv'
with open(csv_name) as csvfile:
    csv_data = pd.read_csv(csvfile)  # header=1默然不读取表头
    csv_data.dropna(inplace=True, subset=['SOC', '总电压'])  # 删除SOC为缺失值的行
    csv_data.reset_index(drop=True, inplace=True)

ls = []
ls_son = []
for i in range(csv_data.shape[0]):
    if csv_data['充电状态'][i] == 3 and csv_data['累计里程'][i] != None:
        if np.isnan(csv_data['累计里程'][i]):
            continue
        ls_son.append(i)
    elif csv_data['充电状态'][i] == 1:
        if len(ls_son) > 300:
            ls.append(ls_son)
        ls_son = []
for index in ls[0:1]:
    data = csv_data.iloc[index, :]
    data.reset_index(drop=True, inplace=True)
    data['累计里程'] = abs(data['累计里程'] - data['累计里程'].tolist()[-1])
    s1 = []
    s2 = []
    for i in range(len(index)):
        s1.append(float(data['SOC'].tolist()[i] - data['SOC'].tolist()[-1]) / 0.75)
        s2.append(float(data['SOC'].tolist()[i] - data['SOC'].tolist()[-1]) / 1.75)
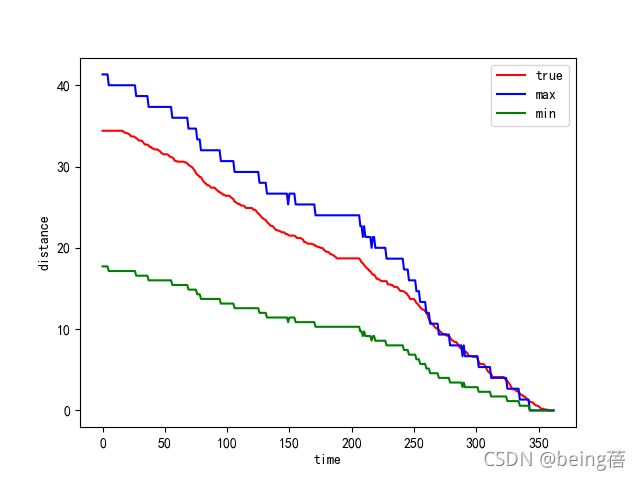
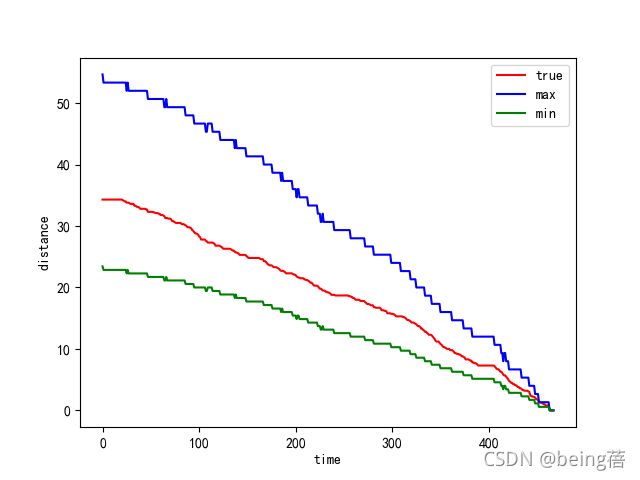
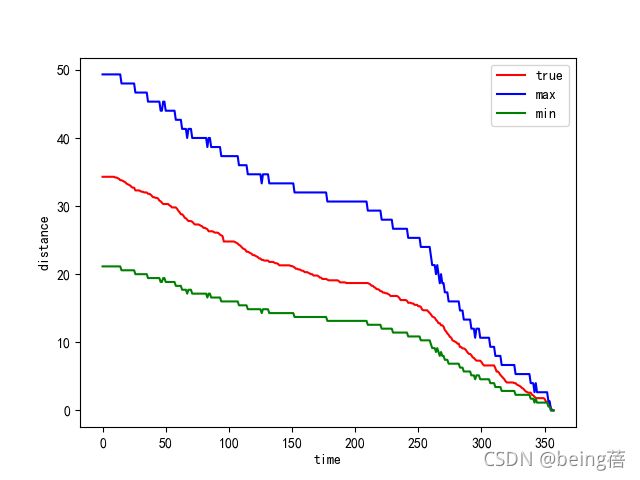
    plt.plot(range(data.shape[0]), data['累计里程'], c='r', label='true')
    plt.plot(range(data.shape[0]), s1, c='b', label='max')
    plt.plot(range(data.shape[0]), s2, c='g', label='min')
    plt.xlabel('time')
    plt.ylabel('distance')
    plt.legend()
    plt.show()

3.2续驶里程和总电压的关系

with open(csv_name) as csvfile:
    csv_data = pd.read_csv(csvfile)  # header=1默然不读取表头
    csv_data.dropna(inplace=True, subset=['SOC', '总电压'])  # 删除SOC为缺失值的行
    csv_data.reset_index(drop=True, inplace=True)

ls = []
ls_son = []
for i in range(csv_data.shape[0]):
    if csv_data['充电状态'][i] == 3 and csv_data['累计里程'][i] != None:
        if np.isnan(csv_data['累计里程'][i]):
            continue
        ls_son.append(i)
    elif csv_data['充电状态'][i] == 1:
        if len(ls_son) > 300:
            ls.append(ls_son)
        ls_son = []
corr_list= []
for index in ls:
    data = csv_data.iloc[index, :]
    data.reset_index(drop=True, inplace=True)
    data['累计里程'] = abs(data['累计里程'] - data['累计里程'].tolist()[-1])

    correlation = data['累计里程'].corr(data['总电压'])
    corr_list.append(correlation)

plt.plot(range(len(corr_list)), corr_list)
plt.xlabel('sample')
plt.ylabel('correlation')
plt.title('u&mileage correlation')
plt.show()

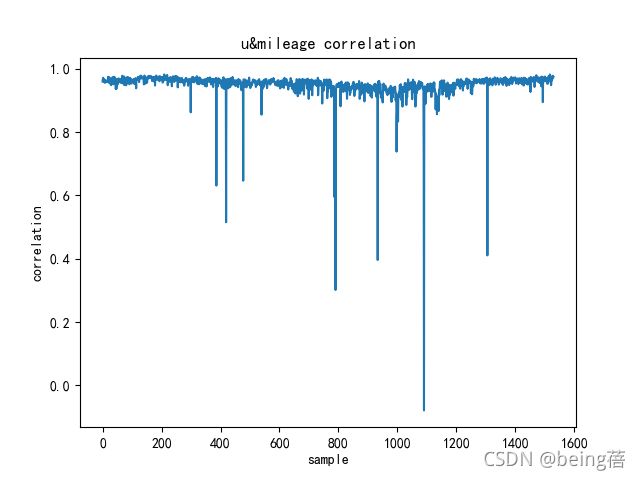
  很明显，基本上每一个周期中总电流和续驶里程之间相关性很高，则假设他们之间存在某种关系。

3.3基于KNN算法对续驶里程进行回归预测

  根据前面得到的最大估计里程、最小估计里程、总电压对电动汽车真实的续航里程进行估计

data=pd.read_csv('../data/mile.csv', header=1)
x = data.iloc[:, 0:3]
y = data.iloc[:, 3:]
# 划分数据集
x_train, x_test, y_train, y_test = train_test_split(x, y, train_size=0.8, random_state=6)
# 标准化处理
x_stand = StandardScaler()
x_train = x_stand.fit_transform(x_train)
x_test = x_stand.transform(x_test)
# 超参数
params = {
    'n_neighbors': [k for k in range(3, 18)],
    'weights': ['uniform', 'distance'],
    'p': [ps for ps in range(2, 8)]
}
kr = KNeighborsRegressor()
# 网格搜索--获取最优参数以及最好的比分
grid_knn = GridSearchCV(estimator=kr, param_grid=params, cv=10)
grid_knn.fit(x_train, y_train)
print('最优参数:', grid_knn.best_params_)
print('最优算法:', grid_knn.best_estimator_)
print('最优评分:', grid_knn.best_score_)
print('测试集评分:', grid_knn.score(x_test, y_test))

  网格搜索后找到最佳参数k=17，对模型进行训练。

kr = KNeighborsRegressor(n_neighbors=17)
kr.fit(x_train, y_train)
y_pre = kr.predict(x_test)
mse = np.sqrt(mean_squared_error(y_test, y_pre))
print('均方误差:', mse)
print('测试集评分:', r2_score(y_test, y_pre))
x_index = [i for i in range(x_test.shape[0])]
print(x_index)
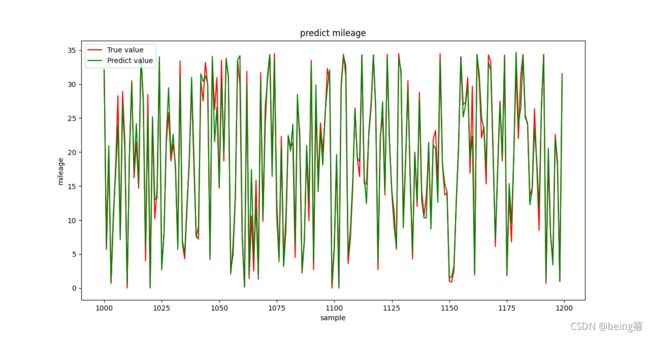
plt.figure()
plt.title('predict mileage')
plt.plot(x_index[1000:1200], y_test[1000:1200], c='r', label="True value")
plt.plot(x_index[1000:1200], y_pre[1000:1200], c='g', label="Predict value")
plt.xlabel('sample')
plt.ylabel('mileage')
plt.legend(loc="best")
plt.show()

  训练后得到均方误差为2.44，R2为0.945，截取部分测试集绘图发现，真实值和预测值基本吻合，整个模型的效果还是比较可以。

4.扩展

  对平均能耗进行滤波处理后，发现其类似一条平滑的曲线，是否可以依据时间进行分类分析？