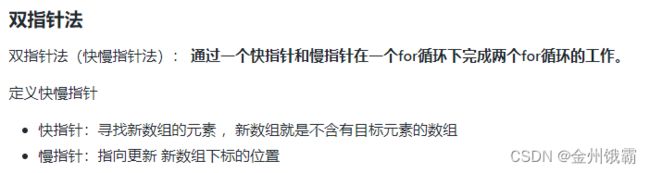
力扣刷题(代码回忆录)——数组部分
数组
- 数组过于简单,但你该了解这些!
- 数组:二分查找
- 数组:移除元素
- 数组:序数组的平方
- 数组:长度最小的子数组
- 数组:螺旋矩阵II
- 数组:总结篇
704. 二分查找
给定一个 n 个元素有序的(升序)整型数组 nums 和一个目标值 target ,写一个函数搜索 nums 中的 target,如果目标值存在返回下标,否则返回 -1。
示例 1:
输入: nums = [-1,0,3,5,9,12], target = 9
输出: 4
解释: 9 出现在 nums 中并且下标为 4示例 2:
输入: nums = [-1,0,3,5,9,12], target = 2
输出: -1
解释: 2 不存在 nums 中因此返回 -1提示:
- 你可以假设
nums中的所有元素是不重复的。 n将在[1, 10000]之间。nums的每个元素都将在[-9999, 9999]之间。
算法思路: 二分查找模板
class Solution {
public:
int search(vector& nums, int target) {
int left = 0;
int right = nums.size() - 1; // 定义target在左闭右闭的区间里,[left, right]
while (left <= right) { // 当left==right,区间[left, right]依然有效,所以用 <=
int middle = left + ((right - left) / 2);// 防止溢出 等同于(left + right)/2
if (nums[middle] > target) {
right = middle - 1; // target 在左区间,所以[left, middle - 1]
} else if (nums[middle] < target) {
left = middle + 1; // target 在右区间,所以[middle + 1, right]
} else { // nums[middle] == target
return middle; // 数组中找到目标值,直接返回下标
}
}
// 未找到目标值
return -1;
}
}; 实现代码:
class Solution:
def search(self, nums: List[int], target: int) -> int:
left, right = 0, len(nums)-1
while(left <= right):
mid = int((left + right) / 2)
if(nums[mid] == target):
return mid
elif(nums[mid] > target):
right = mid - 1
else:
left = mid + 1
return -1类似的二分查找的题目:
类似题目1:35. 搜索插入位置
给定一个排序数组和一个目标值,在数组中找到目标值,并返回其索引。如果目标值不存在于数组中,返回它将会被按顺序插入的位置。
请必须使用时间复杂度为 O(log n) 的算法。
示例 1:
输入: nums = [1,3,5,6], target = 5
输出: 2示例 2:
输入: nums = [1,3,5,6], target = 2
输出: 1示例 3:
输入: nums = [1,3,5,6], target = 7
输出: 4提示:
1 <= nums.length <= 104-104 <= nums[i] <= 104nums为 无重复元素 的 升序 排列数组-104 <= target <= 104
实现代码:
注意:左指针left指向最小大于target的值(也叫target右侧最靠近的值),右指针right会指向最大小于target的值(也叫target左侧最靠近的值)。
class Solution:
def searchInsert(self, nums: List[int], target: int) -> int:
left, right = 0, len(nums)-1
while(left <= right):
mid = int((left + right) / 2)
if(nums[mid] == target):
return mid
elif(nums[mid] > target):
right = mid - 1#右指针会指向最大小于target的值
else:
left = mid + 1#左指针指向最小大于target的值
return left 类似题目2 :34. 在排序数组中查找元素的第一个和最后一个位置(题目很新)
给你一个按照非递减顺序排列的整数数组 nums,和一个目标值 target。请你找出给定目标值在数组中的开始位置和结束位置。
如果数组中不存在目标值 target,返回 [-1, -1]。
你必须设计并实现时间复杂度为 O(log n) 的算法解决此问题。
示例 1:
输入:nums = [5,7,7,8,8,10], target = 8
输出:[3,4]示例 2:
输入:nums = [5,7,7,8,8,10], target = 6
输出:[-1,-1]示例 3:
输入:nums = [], target = 0
输出:[-1,-1]提示:
0 <= nums.length <= 105-109 <= nums[i] <= 109nums是一个非递减数组-109 <= target <= 109
算法分析:
寻找target在数组里的左右边界,有如下三种情况:
- 情况一:target 在数组范围的右边或者左边,例如数组{3, 4, 5},target为2或者数组{3, 4, 5},target为6,此时应该返回{-1, -1}
- 情况二:target 在数组范围中,且数组中不存在target,例如数组{3,6,7},target为5,此时应该返回{-1, -1}
- 情况三:target 在数组范围中,且数组中存在target,例如数组{3,6,7},target为6,此时应该返回{1, 1}
这三种情况都考虑到,说明就想的很清楚了。
接下来,在去寻找左边界,和右边界了。
采用二分法来去寻找左右边界,为了让代码清晰,我分别写两个二分来寻找左边界和右边界。
实现代码:
class Solution:
def searchRange(self, nums: List[int], target: int) -> List[int]:
if(len(nums) == 0):
return [-1, -1]
def findLeftBound(nums, target):#找到左边界
left, right = 0, len(nums)-1
while(left <= right):
mid = int(left+(right-left)/2)
if(nums[mid] == target):
# 为了找到左边界,在遇到target值的时候还要继续往左边找
right = mid -1
elif(nums[mid] > target):
right = mid - 1#右指针会指向最大小于target的值
else:
left = mid + 1#左指针指向最小大于target的值
if(left >= len(nums) or nums[left] != target):
return -1
else:
return left
def findRightBound(nums, target):#找到右边界
left, right = 0, len(nums)-1
while(left <= right):
mid = int(left+(right-left)/2)
if(nums[mid] == target):
# 为了找到右边界,在遇到target值的时候还要继续往左边找
left = mid + 1
elif(nums[mid] > target):
right = mid - 1#右指针会指向最大小于target的值
else:
left = mid + 1#左指针指向最小大于target的值
if(right < 0 or nums[right] != target):
return -1
else:
return right
leftBound = findLeftBound(nums, target)
rightBoud = findRightBound(nums, target)
return[leftBound, rightBoud]
类似题目3:69. x 的平方根
给你一个非负整数 x ,计算并返回 x 的 算术平方根 。
由于返回类型是整数,结果只保留 整数部分 ,小数部分将被 舍去 。
注意:不允许使用任何内置指数函数和算符,例如 pow(x, 0.5) 或者 x ** 0.5 。
示例 1:
输入:x = 4
输出:2示例 2:
输入:x = 8
输出:2
解释:8 的算术平方根是 2.82842..., 由于返回类型是整数,小数部分将被舍去。提示:
0 <= x <= 231 - 1
算法思想:
由于 x 平方根的整数部分 ans 是满足 k ^ 2 ≤ x 的最大 k 值,因此我们可以对 k 进行二分查找,从而得到答案。
二分查找的下界为 0,上界可以粗略地设定为 x。在二分查找的每一步中,我们只需要比较中间元素 mid 的平方与 x 的大小关系,并通过比较的结果调整上下界的范围。
实现代码:
class Solution:
def mySqrt(self, x: int) -> int:
left, right = 0, x
while(left <= right):
mid = (left + right) // 2 #//表示向下取整
if(mid **2 == x):
return mid
elif(mid **2 < x):
left = mid + 1#左指针指向最小大于target的值
else:
right = mid - 1#右指针会指向最大小于target的值
return right类似题目4:367. 有效的完全平方数
给定一个 正整数 num ,编写一个函数,如果 num 是一个完全平方数,则返回 true ,否则返回 false 。
进阶:不要 使用任何内置的库函数,如 sqrt 。
示例 1:
输入:num = 16
输出:true示例 2:
输入:num = 14
输出:false提示:
1 <= num <= 2^31 - 1
实现代码:(算法思路跟这个题目69. x 的平方根一样):
class Solution:
def isPerfectSquare(self, num: int) -> bool:
left, right = 1, num
while(left <= right):
mid = (left + right) // 2
if(mid **2 == num):
return True
elif(mid **2 < num):
left = mid + 1
else:
right = mid - 1
return False127. 移除元素-双指针法(快慢指针法)
给你一个数组 nums 和一个值 val,你需要 原地 移除所有数值等于 val 的元素,并返回移除后数组的新长度。
不要使用额外的数组空间,你必须仅使用 O(1) 额外空间并 原地 修改输入数组。
元素的顺序可以改变。你不需要考虑数组中超出新长度后面的元素。
算法思想:
实现代码:
class Solution:
def removeElement(self, nums: List[int], val: int) -> int:
#双指针左移覆盖法
left = 0#左指针left 指向下一个将要赋值的位置
for right in range(len(nums)):#右指针 right指向当前将要处理的元素
if(nums[right] != val):
nums[left] = nums[right]
left += 1
return left类似题目1 26. 删除有序数组中的重复项 - 双指针之快慢指针
给你一个 升序排列 的数组 nums ,请你 原地 删除重复出现的元素,使每个元素 只出现一次 ,返回删除后数组的新长度。元素的 相对顺序 应该保持 一致 。
由于在某些语言中不能改变数组的长度,所以必须将结果放在数组nums的第一部分。更规范地说,如果在删除重复项之后有 k 个元素,那么 nums 的前 k 个元素应该保存最终结果。
将最终结果插入 nums 的前 k 个位置后返回 k 。
不要使用额外的空间,你必须在 原地 修改输入数组 并在使用 O(1) 额外空间的条件下完成。
解题思路:
题意:删除有序数组重复项,把去重后的数字放在输入数组的前面 n 个位置,返回 n.
看到题目标题的第一反应,当然是用 set !set 就是为了实现去重的。但是题目要求我们进行原地操作,并且时间复杂度是 O(1),因此就不能开辟另外的空间。
双指针:
题目需要我们把去重后的结果保存到原本的数组中,所以想到必须有一个指针指向当前需要把结果放在哪个位置。还要一个指针指向当前应该放到哪个元素。
- 慢指针作为基准,快指针用于寻找与慢指针不同的元素。
- 如果快指针和慢指针指向的元素不等,则把快指针指向的元素放到慢指针的下一个位置。
- 慢指针右移,把新的元素作为基准。
实现代码:
class Solution:
def removeDuplicates(self, nums: List[int]) -> int:
left = 0#慢指针
for right in range(1, len(nums)):#right表示快指针
if(nums[left] != nums[right]):
#如果快指针和慢指针指向的元素不等,则把快指针指向的元素放到慢指针的下一个位置。
left += 1
nums[left] = nums[right]
return left+1类似题目2 283. 移动零
给定一个数组 nums,编写一个函数将所有 0 移动到数组的末尾,同时保持非零元素的相对顺序。
请注意 ,必须在不复制数组的情况下原地对数组进行操作。
实现代码:(算法思想同 类似题目1 26. 删除有序数组中的重复项 )
class Solution:
def moveZeroes(self, nums: List[int]) -> None:
"""
Do not return anything, modify nums in-place instead.
"""
left = 0
for right in range(len(nums)):
if(nums[right] != 0):
nums[left] = nums[right]
left += 1
for i in range(left, len(nums)):
nums[i] = 0类似题目3:977. 有序数组的平方
给你一个按 非递减顺序 排序的整数数组 nums,返回 每个数字的平方 组成的新数组,要求也按 非递减顺序 排序。
示例 1:
输入:nums = [-4,-1,0,3,10]
输出:[0,1,9,16,100]
解释:平方后,数组变为 [16,1,0,9,100]
排序后,数组变为 [0,1,9,16,100]示例 2:
输入:nums = [-7,-3,2,3,11]
输出:[4,9,9,49,121]提示:
1 <= nums.length <= 104-104 <= nums[i] <= 104nums已按 非递减顺序 排序
算法分析:
同样地,我们可以使用两个指针分别指向位置 000 和 n−1n-1n−1,每次比较两个指针对应的数,选择较大的那个逆序放入答案并移动指针。
实现代码:
class Solution:
def sortedSquares(self, nums: List[int]) -> List[int]:
# for i in range(len(nums)):
# nums[i] = nums[i]**2
# nums = sorted(nums)
# return nums
res = [0 for _ in range(len(nums))]
left, right, pos = 0, len(nums)-1, len(nums)-1
#从最后开始放较大的那个数字
#因为left或者right开始的时候一定是指向那个平方最大的那个数
while(left <= right):
if((nums[left] **2) > (nums[right] **2)):
res[pos] = nums[left] **2
left += 1
else:
res[pos] = nums[right] **2
right -= 1
pos -= 1
return res类似题目4:844. 比较含退格的字符串
给定 s 和 t 两个字符串,当它们分别被输入到空白的文本编辑器后,如果两者相等,返回 true 。# 代表退格字符。
注意:如果对空文本输入退格字符,文本继续为空。
示例 1:
输入:s = "ab#c", t = "ad#c"
输出:true
解释:s 和 t 都会变成 "ac"。示例 2:
输入:s = "ab##", t = "c#d#"
输出:true
解释:s 和 t 都会变成 ""。示例 3:
输入:s = "a#c", t = "b"
输出:false
解释:s 会变成 "c",但 t 仍然是 "b"。提示:
1 <= s.length, t.length <= 200s和t只含有小写字母以及字符'#'
算法分析:
采用类似栈的思想,当字符串s或者t的第i个字符不为空时,就把第i个字符入栈,当第i个字符为#时,就把栈顶元素弹出(前提时栈不为空时才可以进行此操作),最后再把栈里的元素转化为字符串再比较两者是否相等。
实现代码:
class Solution:
def backspaceCompare(self, s: str, t: str) -> bool:
listS = []
for i in range(len(s)):
if(s[i] != '#'):
listS.append(s[i])
else:
if(len(listS) != 0):#当列表不为空时,才能弹出元素
listS.pop()
s = ''.join(listS)#列表类型转化为字符串类型
listT = []
for i in range(len(t)):
if(t[i] != '#'):
listT.append(t[i])
else:
if(len(listT) != 0):#当列表不为空时,才能弹出元素
listT.pop()
t = ''.join(listT)#列表类型转化为字符串类型
return s == t类似题目5:15. 三数之和 -三指针+排序
给你一个整数数组 nums ,判断是否存在三元组 [nums[i], nums[j], nums[k]] 满足 i != j、i != k 且 j != k ,同时还满足 nums[i] + nums[j] + nums[k] == 0 。请
你返回所有和为 0 且不重复的三元组。
注意:答案中不可以包含重复的三元组。
示例 1:
输入:nums = [-1,0,1,2,-1,-4]
输出:[[-1,-1,2],[-1,0,1]]
解释:
nums[0] + nums[1] + nums[2] = (-1) + 0 + 1 = 0 。
nums[1] + nums[2] + nums[4] = 0 + 1 + (-1) = 0 。
nums[0] + nums[3] + nums[4] = (-1) + 2 + (-1) = 0 。
不同的三元组是 [-1,0,1] 和 [-1,-1,2] 。
注意,输出的顺序和三元组的顺序并不重要。示例 2:
输入:nums = [0,1,1]
输出:[]
解释:唯一可能的三元组和不为 0 。示例 3:
输入:nums = [0,0,0]
输出:[[0,0,0]]
解释:唯一可能的三元组和为 0 。提示:
3 <= nums.length <= 3000-105 <= nums[i] <= 105
算法思想:
实现代码:
class Solution:
def threeSum(self, nums: List[int]) -> List[List[int]]:
res = []
if(not nums or len(nums) < 3 ):
return []
nums.sort()
for i in range(len(nums)):
# 若 nums[i]>0:因为已经排序好,所以后面不可能有三个数加和等于 0,直接返回[]
if(nums[i] > 0):
break
# 对于重复元素:跳过,避免出现重复解
if(i>0 and nums[i-1] == nums[i]):
continue
l = i+1
r = len(nums)-1
# 令左指针 L=i+1,右指针 R=n-1,当 L 0):
r -= 1
# 若和小于 0,说明 nums[l] 太小,l 右移
else:
l += 1
return res
写法2更利于理解:
class Solution:
def threeSum(self, nums: List[int]) -> List[List[int]]:
res, sum = [], 0
nums.sort()
if(not nums and len(nums) < 3):
return []
for i in range(len(nums)-2):
#在已经排好序的数组且为正数的情况下,当第一个数大于0时,后面的情况可以不用看了
if(nums[i] > 0):#剪枝
break
l = i + 1
r = len(nums) - 1
while(l < r):
sum = nums[i] + nums[l] + nums[r]
if(sum == 0 and [nums[i],nums[l],nums[r]] not in res):
res.append([nums[i], nums[l], nums[r]])
l += 1
r -= 1
elif(sum > 0):
r -= 1
else:
l += 1
return res类似题目6:18. 四数之和
给你一个由 n 个整数组成的数组 nums ,和一个目标值 target 。请你找出并返回满足下述全部条件且不重复的四元组 [nums[a], nums[b], nums[c], nums[d]] (若两个四元组元素一一对应,则认为两个四元组重复):
0 <= a, b, c, d < na、b、c和d互不相同nums[a] + nums[b] + nums[c] + nums[d] == target
你可以按 任意顺序 返回答案 。
示例 1:
输入:nums = [1,0,-1,0,-2,2], target = 0
输出:[[-2,-1,1,2],[-2,0,0,2],[-1,0,0,1]]示例 2:
输入:nums = [2,2,2,2,2], target = 8
输出:[[2,2,2,2]]提示:
1 <= nums.length <= 200-109 <= nums[i] <= 109-109 <= target <= 109
算法思路:
本质上同15. 三数之和算法如出一辙,只是在原来的基础上又套了一层for循环
实现代码:
class Solution:
def fourSum(self, nums: List[int], target: int) -> List[List[int]]:
res, sum = [], 0
nums.sort()
if(not nums and len(nums) < 4):
return []
for i in range(len(nums)-3):
#在已经排好序的数组且为正数的情况下,当第一个数大于target时,后面的情况可以不用看了
if(nums[i] > 0 and nums[i] > target):#剪枝
break
for j in range(i+1, len(nums)-2):
l = j + 1
r = len(nums) - 1
while(l < r):
sum = nums[i] + nums[j] + nums[l] + nums[r]
if(sum == target and [nums[i],nums[j],nums[l],nums[r]] not in res):
res.append([nums[i],nums[j],nums[l],nums[r]])
l += 1
r -= 1
elif(sum > target):
r -= 1
else:
l += 1
return res
209. 长度最小的子数组-滑动窗口
滑动窗口模板:
def findSubArray(nums):
N = len(nums) # 数组/字符串长度
left, right = 0, 0 # 双指针,表示当前遍历的区间[left, right],闭区间
sums = 0 # 用于统计 子数组/子区间 是否有效,根据题目可能会改成求和/计数
res = 0 # 保存最大的满足题目要求的 子数组/子串 长度
while right < N: # 当右边的指针没有搜索到 数组/字符串 的结尾
sums += nums[right] # 增加当前右边指针的数字/字符的求和/计数
while 区间[left, right]不符合题意: # 此时需要一直移动左指针,直至找到一个符合题意的区间
sums -= nums[left] # 移动左指针前需要从counter中减少left位置字符的求和/计数
left += 1 # 真正的移动左指针,注意不能跟上面一行代码写反
# 到 while 结束时,我们找到了一个符合题意要求的 子数组/子串
res = max(res, right - left + 1) # 需要更新结果
right += 1 # 移动右指针,去探索新的区间
return res
给定一个含有 n 个正整数的数组和一个正整数 target 。
找出该数组中满足其和 ≥ target 的长度最小的 连续子数组 [numsl, numsl+1, ..., numsr-1, numsr] ,并返回其长度。如果不存在符合条件的子数组,返回 0 。
示例 1:
输入:target = 7, nums = [2,3,1,2,4,3]
输出:2
解释:子数组 [4,3] 是该条件下的长度最小的子数组。示例 2:
输入:target = 4, nums = [1,4,4]
输出:1示例 3:
输入:target = 11, nums = [1,1,1,1,1,1,1,1]
输出:0提示:
1 <= target <= 109
1 <= nums.length <= 105
1 <= nums[i] <= 105
算法思路:
将数组nums里的元素依次一个个入队window,要是sum(window)超过target值就减掉一个,要是没超过就继续加,直至满足条件。
实现代码:
class Solution:
def minSubArrayLen(self, target: int, nums: List[int]) -> int:
left = right = 0 #滑动窗口的左右两个端点
minLen = float('inf') #初始化长度最小的 连续子数组的长度
sum = 0 #记录当前窗口里元素的之和
length = len(nums) #记录列表里元素的个数
while(right < length):
sum += nums[right]
while(sum >= target):
sum -= nums[left] # 去掉左侧的数
minLen = min(minLen, right - left + 1)
left += 1 # 左边要剔除的数可能不止一个
right += 1
if(minLen == float('inf')): #target值不在列表里
return 0
else:
return minLen更多滑动窗口题目和内容可以参考:
力扣---字符串系列题目_金州饿霸的博客-CSDN博客
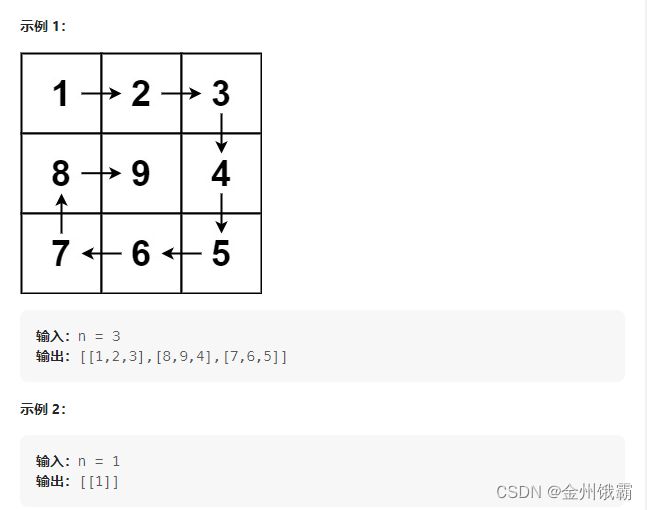
59. 螺旋矩阵 II-四指针(上下左右)边界收缩
给你一个正整数 n ,生成一个包含 1 到 n2 所有元素,且元素按顺时针顺序螺旋排列的 n x n 正方形矩阵 matrix 。
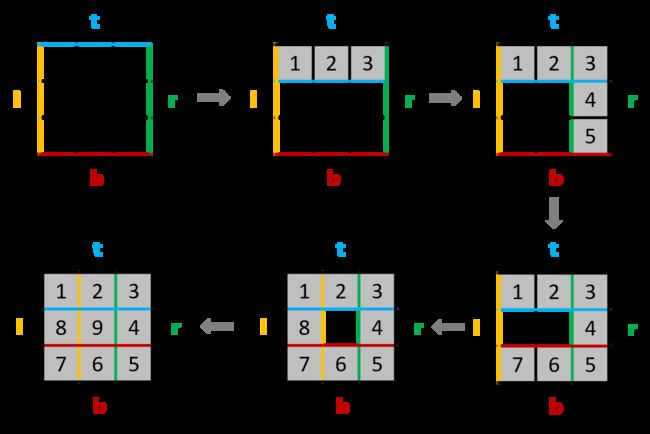
算法思路:(本质是把数顺时针填入矩阵中)
实现代码:
class Solution:
def generateMatrix(self, n: int) -> List[List[int]]:
l, r, t, b = 0, n - 1, 0, n - 1#左右上下的边界, 同时t/l也表示行,b/r也表示列
res = [[0 for _ in range(n)] for _ in range(n)]
num = 1#表示要填充的数字
while(num <= n**2):
for i in range(l, r + 1):# 从左到右填充,相当于缩小上边界
res[t][i] = num
num += 1
t += 1#从左到右填完后,上边界 t += 1,相当于上边界向内缩 1
for i in range(t, b + 1):#从上向下填充,相当于缩小右边界
res[i][r] = num
num += 1
r -= 1
for i in range(r, l-1, -1):# 从右向左填充,相当于缩小下边界
res[b][i] = num
num += 1
b -= 1
for i in range(b, t-1, -1):# 从下向上填充,相当于缩小左边界
res[i][l] = num
num += 1
l += 1
return res
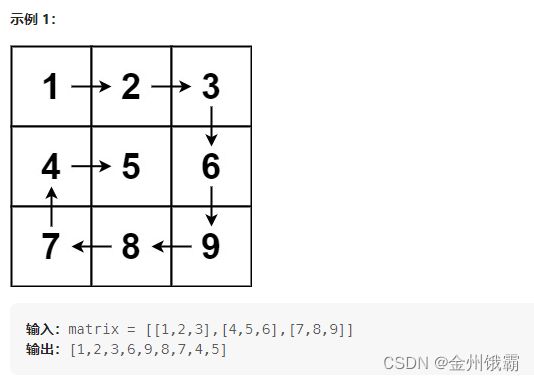
类似题目1:54. 螺旋矩阵
给你一个 m 行 n 列的矩阵 matrix ,请按照 顺时针螺旋顺序 ,返回矩阵中的所有元素。
算法思想:(本质上是把矩阵里的数顺时针读出来)
算法思想同上面的题目59. 螺旋矩阵 II
实现代码:
class Solution:
def spiralOrder(self, matrix: List[List[int]]) -> List[int]:
l, r, t, b = 0, len(matrix[0]) - 1, 0, len(matrix) - 1
res = []
length = len(matrix[0]) * len(matrix) #矩阵元素个数(列*行)
while(length > 0):
for i in range(l, r + 1):# 从左到右填充,相当于缩小上边界
if(length > 0):
res.append(matrix[t][i])
length -= 1
t += 1#从左到右填完后,上边界 t += 1,相当于上边界向内缩 1
for i in range(t, b + 1):#从上向下填充,相当于缩小右边界
if(length > 0):
res.append(matrix[i][r])
length -= 1
r -= 1
for i in range(r, l-1, -1):# 从右向左填充,相当于缩小下边界
if(length > 0):
res.append(matrix[b][i])
length -= 1
b -= 1
for i in range(b, t-1, -1):# 从下向上填充,相当于缩小左边界
if(length > 0):
res.append(matrix[i][l])
length -= 1
l += 1
return res回溯算法
46. 全排列
给定一个不含重复数字的数组 nums ,返回其 所有可能的全排列 。你可以 按任意顺序 返回答案。
示例 1:
输入:nums = [1,2,3]
输出:[[1,2,3],[1,3,2],[2,1,3],[2,3,1],[3,1,2],[3,2,1]]示例 2:
输入:nums = [0,1]
输出:[[0,1],[1,0]]示例 3:
输入:nums = [1]
输出:[[1]]提示:
1 <= nums.length <= 6-10 <= nums[i] <= 10nums中的所有整数 互不相同
算法思想:
(1)方法一:调用库函数
利用itertools库中的permutations方法。
实现代码:
class Solution:
def permute(self, nums: List[int]) -> List[List[int]]:
all_permutation = list(itertools.permutations(nums))
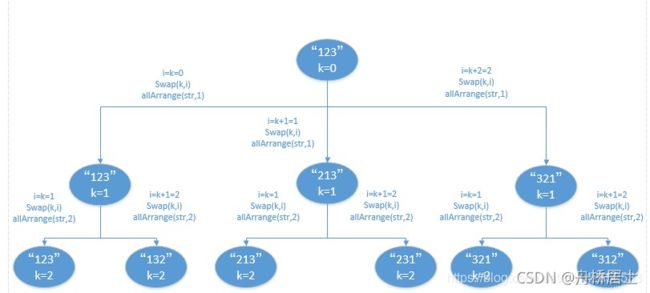
return all_permutation(2)方法二:递归法 (下面是全排列的模板可以记住)
实现代码:
class Solution:
def permute(self, nums: List[int]) -> List[List[int]]:
def backtrack(position, end):
if position == end:
res.append(nums[:])
else:
for index in range(position, end):
nums[index], nums[position] = nums[position], nums[index]#交换两个值的位置
backtrack(position + 1, end)
nums[index], nums[position] = nums[position], nums[index]
res = []
backtrack(0, len(nums))
return res
47. 全排列 II
给定一个可包含重复数字的序列 nums ,按任意顺序 返回所有不重复的全排列。
示例 1:
输入:nums = [1,1,2]
输出:
[[1,1,2],
[1,2,1],
[2,1,1]]示例 2:
输入:nums = [1,2,3]
输出:[[1,2,3],[1,3,2],[2,1,3],[2,3,1],[3,1,2],[3,2,1]]
提示:
1 <= nums.length <= 8
-10 <= nums[i] <= 10
算法思路:
(1)方法一:库函数➕set集合剪枝去重
这题主要是在全排列的基础上减枝,就是将全排列的结果重复的排列去除掉(因为给的元素可能有重复值),所以可以用集合set去除重复值,然后再转为list值。
实现代码:
class Solution:
def permuteUnique(self, nums: List[int]) -> List[List[int]]:
all_permutation = list(itertools.permutations(nums))
res = set(all_permutation)
return list(res)(2)方法二:递归+剪枝去重
去重主要靠这一步:
nums[:] not in resclass Solution:
def permuteUnique(self, nums: List[int]) -> List[List[int]]:
def backtrack(position, end):
if(position == end and nums[:] not in res):#减枝去重复
res.append(nums[:])
else:
for index in range(position, end):
nums[index], nums[position] = nums[position], nums[index]#交换两个值的位置
backtrack(position + 1, end)
nums[index], nums[position] = nums[position], nums[index]
res = []
backtrack(0, len(nums))
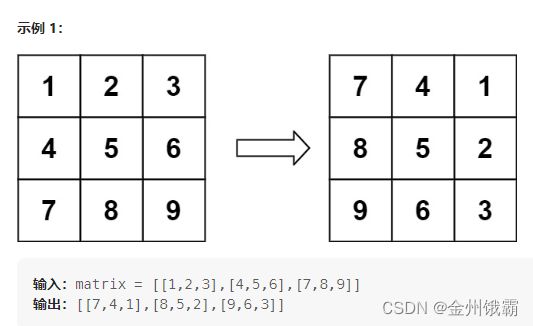
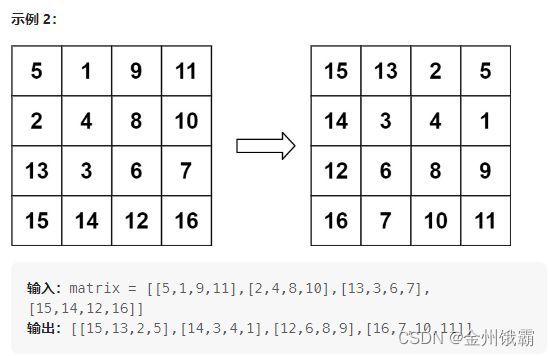
return res48. 旋转图像
给定一个 n × n 的二维矩阵 matrix 表示一个图像。请你将图像顺时针旋转 90 度。
你必须在 原地 旋转图像,这意味着你需要直接修改输入的二维矩阵。请不要 使用另一个矩阵来旋转图像。
算法思想:
(1)方法一:
直接开辟一个O(n^2)的空间,然后按自下而上,自左到右的顺序遍历,最终把结果存起来。
实现代码:
class Solution:
def rotate(self, matrix: List[List[int]]) -> None:
"""
Do not return anything, modify matrix in-place instead.
"""
res = []
for j in range(len(matrix[0])):#控制矩阵的列
temp = []
for i in range(len(matrix)-1, -1, -1):#逆序按行遍历
temp.append(matrix[i][j])
res.append(temp)
for i in range(len(matrix)):
for j in range(len(matrix[0])):
matrix[i][j] = res[i][j](2)方法二:
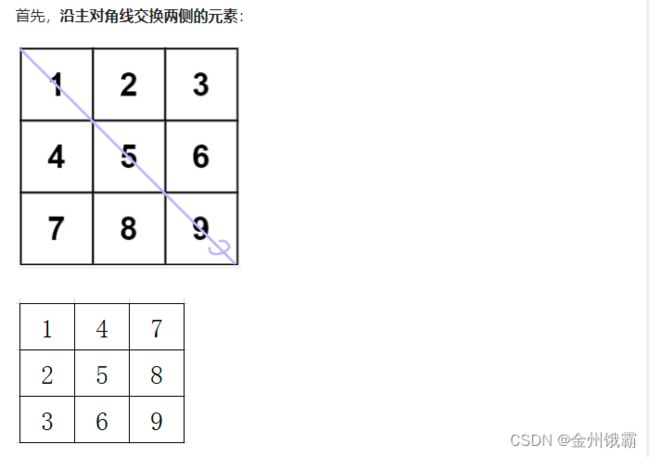
对于一个矩阵,要一层一层旋转90°实现起来很复杂。不妨先想想,对于矩阵中值的交换,有哪些操作是比较方便的:
- 对单行或单列元素反转
- 沿对角线交换对角线两侧的元素
实现代码:
class Solution:
def rotate(self, matrix: List[List[int]]) -> None:
"""
Do not return anything, modify matrix in-place instead.
"""
for i in range(len(matrix)):#交换对角线两边的元素
# 注意这里j的范围 如果j的范围也是0到n-1那么会出现交换后又交换回来等于没有交换
for j in range(i):
matrix[i][j], matrix[j][i] = matrix[j][i], matrix[i][j]
for line in matrix:#按行取反
line.reverse()78. 子集
给你一个整数数组 nums ,数组中的元素 互不相同 。返回该数组所有可能的子集(幂集)。
解集 不能 包含重复的子集。你可以按 任意顺序 返回解集。
示例 1:
输入:nums = [1,2,3]
输出:[[],[1],[2],[1,2],[3],[1,3],[2,3],[1,2,3]]示例 2:
输入:nums = [0]
输出:[[],[0]]
提示:
1 <= nums.length <= 10-10 <= nums[i] <= 10nums中的所有元素 互不相同
算法思想:
有一种思想比较巧妙,可以叫按位对应法。如集合A={a,b,c},对于任意一个元素,在每个子集中,要么存在,要么不存在。也就是说n个元素的集合,它一共有2^n个子集,那么这2^n子集对应整数为0-2^n-1,这些整数可以用n位的二进制数来表示,并且每个子集中的元素存在与否也可以用这n位来表示,1表示在子集中,0表示不在子集中。
映射为子集:
类似的图解:
![]()
实现代码:
class Solution:
def subsets(self, nums: List[int]) -> List[List[int]]:
res = []
for i in range(2 ** len(nums)):#n个元素的集合共有2^n个子集
temp = []#存放一个子集
for j in range(len(nums)):#n位二进制数来表示一个子集里的元素,1表示该元素在子集里,0表示不在子集里
if((i >> j) % 2 == 1):#按位对应,看每一位是否为1,为1表示该元素在子集中,那么就加入temp
temp.append(nums[j])
res.append(temp)
return res90. 子集 II
给你一个整数数组 nums ,其中可能包含重复元素,请你返回该数组所有可能的子集(幂集)。
解集 不能 包含重复的子集。返回的解集中,子集可以按 任意顺序 排列。
示例 1:
输入:nums = [1,2,2]
输出:[[],[1],[1,2],[1,2,2],[2],[2,2]]示例 2:
输入:nums = [0]
输出:[[],[0]]提示:
1 <= nums.length <= 10-10 <= nums[i] <= 10
算法思想:
跟上面的思路一模一样,只不过多了一个排序去重的步骤:
finalRes = []
for i in range(len(res)):
res[i] = sorted(res[i])
for i in range(len(res)):
if(res[i] not in finalRes):
finalRes.append(res[i])实现代码:
class Solution:
def subsetsWithDup(self, nums: List[int]) -> List[List[int]]:
res = []
for i in range(2 ** len(nums)):#n个元素的集合共有2^n个子集
temp = []#存放一个子集
for j in range(len(nums)):#n位二进制数来表示一个子集里的元素,1表示该元素在子集里,0表示不在子集里
if((i >> j) % 2 == 1):#按位对应,看每一位是否为1,为1表示该元素在子集中,那么就加入temp
temp.append(nums[j])
res.append(temp)#res里面可能有重复的子集,只不过因为元素的顺序不同而看着不一样
finalRes = []
for i in range(len(res)):#排序去重
res[i] = sorted(res[i])
for i in range(len(res)):#去重
if(res[i] not in finalRes):
finalRes.append(res[i])
return finalRes