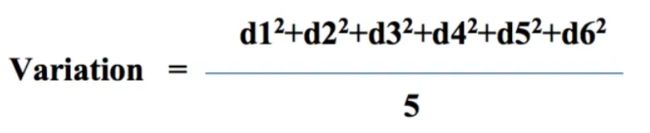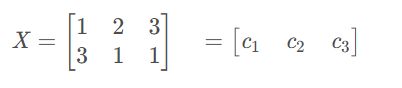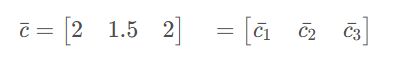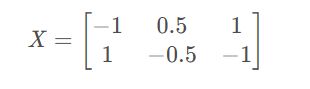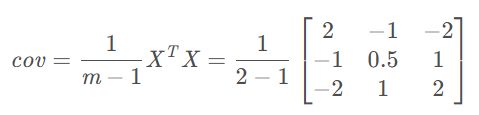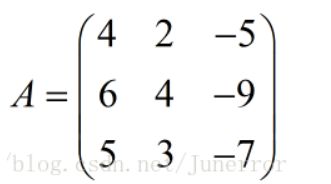PCA（主成分分析）的理解与应用（学习笔记）

PCA

        主成分分析（Principal Component Analysis, PCA）是一种线性降维算法，也是一种常用的数据预处理（Pre-Processing）方法。它的目标是是用方差（Variance）来衡量数据的差异性，并将差异性较大的高维数据投影到低维空间中进行表示。绝大多数情况下，我们希望获得两个主成分因子：分别是从数据差异性最大和次大的方向提取出来的，称为PC1(Principal Component 1) 和 PC2（Principal Component 2）。

---

PCA的具体实现

随机选取的六名学生的数学和语文考试成绩

student_id	1	2	3	4	5	6
scores1	92	70	95	73	72	87
scores2	74	87	70	92	97	74

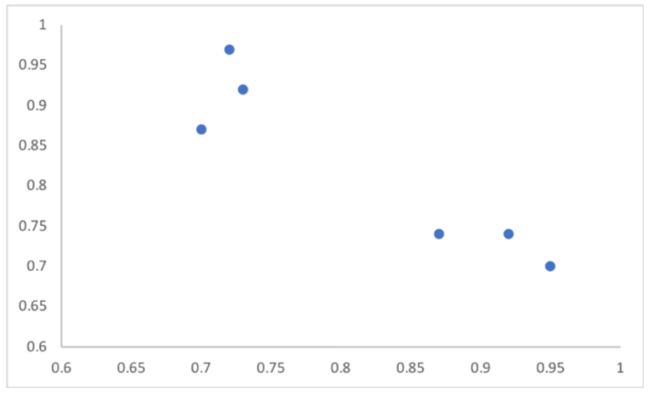
制作为散点图：

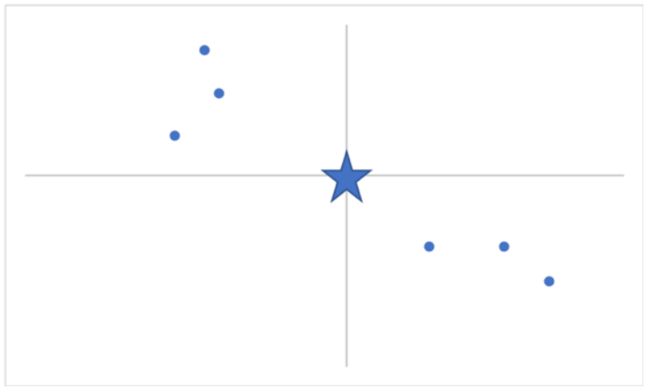
         图中每个点代表了一个学生，X轴代表语文成绩，Y轴代表数学成绩。然后分别取所有样本的X平均值和Y平均值，并将这两个值变为X、Y坐标，在图中画出这个点（用五角星表示）:

         按照图中箭头所示方向，将整个坐标系平移，使原点与五角星重叠。这样就获得了一个新的平面直角坐标系：

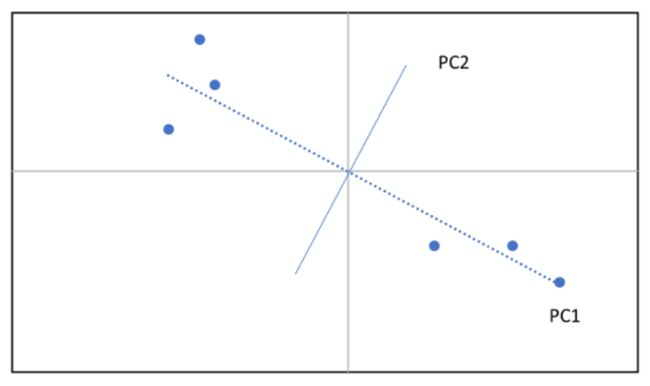
         尽管此时坐标系和每个点的值都发生了变化，点与点之间的相对位置仍保持一致。找到这些点的最优拟合线（Line of Best Fit），也就找到了PC1，再通过原点做PC1的垂线，就找到PC2：

         处理三维数组时便会产生第三个因子（PC3），以此类推，数据的维度越大，因子的数量也就越多。当维度大于等于4的时候，我们是无法想象出图像的，但PC4确实存在；假设有x个维度，便可以做x-1条垂线，就能得到PCx。接下来要做的便是选取最能代表数据差异性的两个因子，作为PC1和PC2。

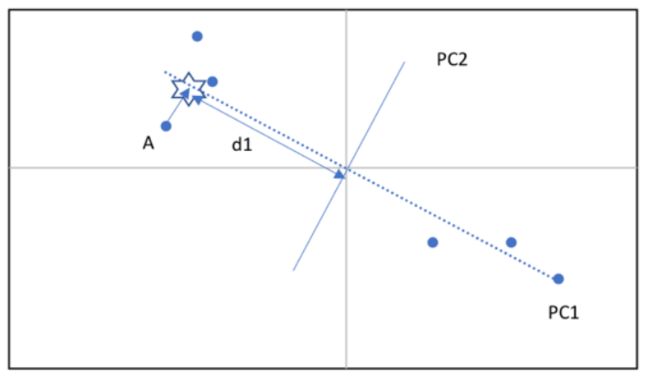
按照下图所示，将点A投影到PC1上（六角星的位置），并计算其与原点之间的距离称为d1：

        其余的五个点也做同样操作，得出d2至d5，再求这六个距离的平方和，称为PC1的特征值（Eigenvalue）。然后将PC1的特征值除以总样本数量减一（n-1），就计算出了PC1的差异值（Variation）。 

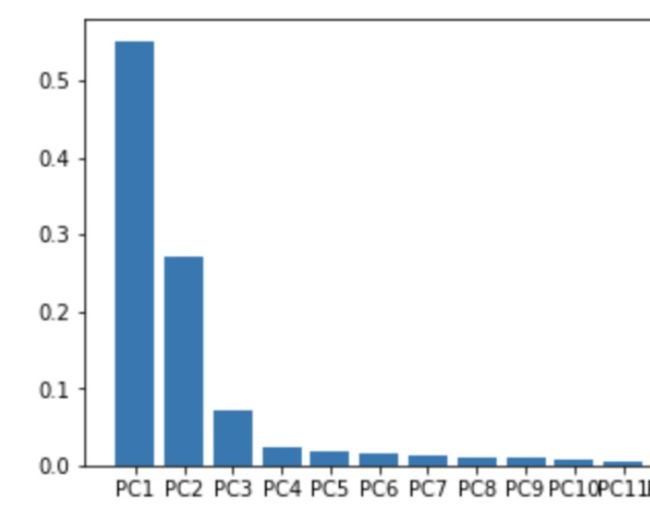
        以此类推，并选择差异值最大的两个因子作为PC1 和 PC2。假设在某个三维数组中，获得了PC1、PC2和PC3的差异值分别为18，7，5。通过计算（18+7）/ (18+7+5) ≈ 83.3% 得到结论：PC1 和 PC2 代表了这个三维数组83.3%的差异性。在本次分析的13个因子中，PC1和PC2描述了整组数据约81%的差异性： 

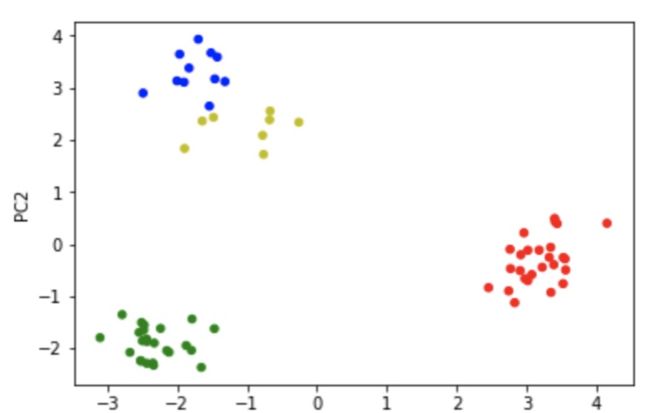
         最后，再通过选中的PC1和PC2将样本映射回本身所在的坐标，就可以得到降维后的图像（PCA Plot）。

---

协方差矩阵基本知识点： 

矩阵中的数据按行排列和按列排列求出的协方差矩阵是不同的，这里默认数据是按行排列。即每一行是一个observation（样本），那么每一列就是一个随机变量（特征）。

举个例子，矩阵X按行排列：

1.求每个维度的平均值

2.将X的每一列减去平均值

 

3.计算协方差矩阵

---

 矩阵特征值和特征向量计算方法：

计算A的特征值和特征向量 

计算行列式得

化简得：

得到特征值：

化简得：

令得到特征矩阵：

同理，当得：

令得到特征矩阵：

---

 代码实现（依次由繁到简实现效果）

方法一：

# -*- coding: utf-8 -*-
"""
@author: 绯雨千叶

用PCA求样本矩阵X的K阶降维矩阵Z
请保证输入的样本矩阵X shape=(m, n)，m行样例，n个特征
"""
import numpy as np

class PCA(object):
    def __init__(self, X, K):
        self.X = X  # 训练样本矩阵X
        self.K = K  # X的降维矩阵的阶数，即X要特征降维成k阶
        self.centrX = []  # 矩阵X的中心化
        self.C = []  # 样本集的协方差矩阵C
        self.U = []  # 样本矩阵X的降维转换矩阵
        self.Z = []  # 样本矩阵X的降维矩阵Z

        self.centrX = self._centralized()
        self.C = self._conv()
        self.U = self._U()
        self.Z = self._Z()  # Z=XU求得

    def _centralized(self):  # 矩阵X的中心化
        print('样本矩阵X:\n', self.X)
        centrX = []
        mean = np.array([np.mean(attr) for attr in self.X.T])  # mean()函数功能：求取均值;样本集的特征均值（每一列的平均数）
        centrX = self.X - mean  # 样本集的中心化(减去他那行的特征均值)
        print('样本集的特征均值:\n', mean)
        print('样本矩阵X的中心化centrX:\n', centrX)
        return centrX

    def _conv(self):  # 求样本矩阵X的协方差矩阵C
        ns = np.shape(self.centrX)[0]  # 样本集的样例总数
        C = np.dot(self.centrX.T, self.centrX) / (ns - 1)  # 样本矩阵的协方差矩阵C;.dot向量点积和矩阵乘法
        print('样本矩阵X的协方差矩阵C:\n', C)
        return C

    def _U(self):  # 求X的降维转换矩阵U, shape=(n,k), n是X的特征维度总数，k是降维矩阵的特征维度
        a, b = np.linalg.eig(self.C)  # 第一个返回值是X的协方差矩阵C的特征值，第二个返回值是特征向量
        print('样本集的协方差矩阵C的特征值:\n', a)
        print('样本集的协方差矩阵C的特征向量:\n', b)
        ind = np.argsort(-1 * a)  # 给出特征值降序的topK的索引序列
        UT = [b[:, ind[i]] for i in range(self.K)]  # 构建K阶降维的降维转换矩阵U
        U = np.transpose(UT)
        print('%d阶降维转换矩阵U:\n' % self.K, U)
        return U

    def _Z(self):  # 按照Z=XU求降维矩阵Z, shape=(m,k), n是样本总数，k是降维矩阵中特征维度总数
        Z = np.dot(self.X, self.U)
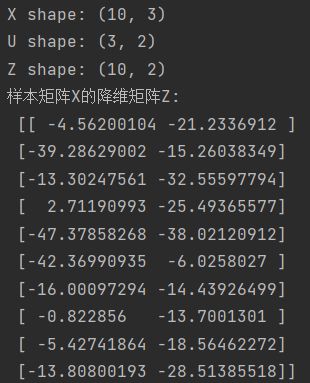
        print('X shape:', np.shape(self.X))
        print('U shape:', np.shape(self.U))
        print('Z shape:', np.shape(Z))
        print('样本矩阵X的降维矩阵Z:\n', Z)
        return Z

if __name__ == '__main__':
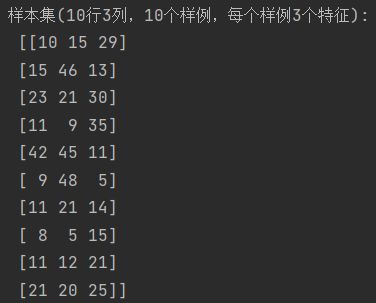
    '10样本3特征的样本集, 行为样例，列为特征维度'
    X = np.array([[10, 15, 29],
                  [15, 46, 13],
                  [23, 21, 30],
                  [11, 9, 35],
                  [42, 45, 11],
                  [9, 48, 5],
                  [11, 21, 14],
                  [8, 5, 15],
                  [11, 12, 21],
                  [21, 20, 25]])
    K = np.shape(X)[1] - 1
    print('样本集(10行3列，10个样例，每个样例3个特征):\n', X)
    pca = PCA(X, K)

效果展示：

 

---

方法二：

# coding=utf-8
"""
@author: 绯雨千叶
"""
import numpy as np

class PCA():
    def __init__(self, n_components):
        self.n_components = n_components

    def fit_transform(self, X):
        self.n_features_ = X.shape[1]
        # 求协方差矩阵
        X = X - X.mean(axis=0)
        self.covariance = np.dot(X.T, X) / X.shape[0]
        # 求协方差矩阵的特征值和特征向量
        eig_vals, eig_vectors = np.linalg.eig(self.covariance)
        # 获得降序排列特征值的序号
        idx = np.argsort(-eig_vals)
        # 降维矩阵
        self.components_ = eig_vectors[:, idx[:self.n_components]]
        # 对X进行降维
        return np.dot(X, self.components_)

# 调用
pca = PCA(n_components=2)
X = np.array(
    [[-1, 2, 66, -1], [-2, 6, 58, -1], [-3, 8, 45, -2], [1, 9, 36, 1], [2, 10, 62, 1], [3, 5, 83, 2]])  # 导入数据，维度为4
newX = pca.fit_transform(X)
print(newX)  # 输出降维后的数据

效果展示： 

---

方法三： 

#coding=utf-8
"""
@author: 绯雨千叶
"""
import numpy as np
from sklearn.decomposition import PCA
X = np.array([[-1,2,66,-1], [-2,6,58,-1], [-3,8,45,-2], [1,9,36,1], [2,10,62,1], [3,5,83,2]])  #导入数据，维度为4
pca = PCA(n_components=2)   #降到2维
pca.fit(X)                  #训练
newX=pca.fit_transform(X)   #降维后的数据
PCA(copy=True, n_components=2, whiten=False)
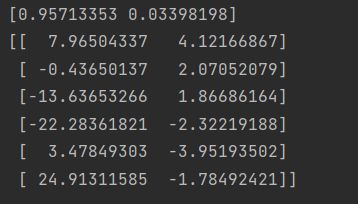
print(pca.explained_variance_ratio_)  #输出贡献率
print(newX)                  #输出降维后的数据

效果展示：

---

sklearn.decomposition.PCA(n_components=None, copy=True, whiten=False)

参数：

n_components:  

意义：PCA算法中所要保留的主成分个数n，也即保留下来的特征个数n

类型：int 或者 string，缺省时默认为None，所有成分被保留。

          赋值为int，比如n_components=1，将把原始数据降到一个维度。

          赋值为string，比如n_components='mle'，将自动选取特征个数n，使得满足所要求的方差百分比。

copy:

类型：bool，True或者False，缺省时默认为True。

意义：表示是否在运行算法时，将原始训练数据复制一份。若为True，则运行PCA算法后，原始训练数据的值不            会有任何改变，因为是在原始数据的副本上进行运算；若为False，则运行PCA算法后，原始训练数据的              值会改，因为是在原始数据上进行降维计算。

whiten:

类型：bool，缺省时默认为False

意义：白化，使得每个特征具有相同的方差。

PCA属性：

• components_ ：返回具有最大方差的成分。
• explained_variance_ratio_：返回 所保留的n个成分各自的方差百分比。
• n_components_：返回所保留的成分个数n。
• mean_：
• noise_variance_：

PCA方法：

1、fit(X,y=None)

fit(X)，表示用数据X来训练PCA模型。

函数返回值：调用fit方法的对象本身。比如pca.fit(X)，表示用X对pca这个对象进行训练。

拓展：fit()可以说是scikit-learn中通用的方法，每个需要训练的算法都会有fit()方法，它其实就是算法中的“训练”这一步骤。因为PCA是无监督学习算法，此处y自然等于None。

2、fit_transform(X)

用X来训练PCA模型，同时返回降维后的数据。

newX=pca.fit_transform(X)，newX就是降维后的数据。

3、inverse_transform()

将降维后的数据转换成原始数据，X=pca.inverse_transform(newX)

4、transform(X)

将数据X转换成降维后的数据。当模型训练好后，对于新输入的数据，都可以用transform方法来降维。

此外，还有get_covariance()、get_precision()、get_params(deep=True)、score(X, y=None)等方法，以后用到再补充吧。