【项目】无人清扫车路径规划:基于ATSP的Lanelet2结构化道路覆盖算法
实习期间一直在做清扫车项目的全局路径规划,在此记录一下。
本文针对Lanelet2框架下的结构化道路全覆盖问题,将其抽象为ATSP问题,进行求解。最终效果为,实现了在全部车道覆盖至少一次的前提下,最短总路径的规划和可视化过程。
代码地址:JK-H/Full_Coverage_With_Lanelet2 at develop (github.com)
目录
前言
一、Lanelet2地图框架
1.1.概述
1.2.地图格式
1.3.Lanelet2地图层次
1.4.Primitives-基础元素
1.5 软件模块(Software Modules)
二、Lanelet2的routing模块
2.1 论文总结
2.1.0 摘要
2.1.1 为什么要考虑寻路Pathfinding问题
2.2.2 Lanelet2如何工作
2.2.3 其他map框架如何表示routing information
2.2.4 一个 Lanelet2 Map 并不是一个 Graph
2.2.5 到底什么是一条 Route
2.2.6 最优路径是一个视角问题
2.2.7 自动驾驶不仅仅是”驾驶“
2.2.8 不是所有东西都是车
2.2 example中Routing部分涉及用法简介
3. 基于Lanelet2的覆盖算法
3.1 按DFS顺序清扫
3.2 抽象为ATSP(非对称旅行商问题)求解清扫顺序
3.2.1 ATSP问题简介
3.2.2 与覆盖算法建立联系
3.2.3 求解方案
3.2.4 算法流程
3.3 运行Demo和效果
4. Lanelet2的routing过程可视化
后记
前言
项目要求在Lanelet2框架的结构化道路上,实现清扫任务的路径规划。起初啥也不懂,肯定先从Lanelet2开始了解,幸好网上相关资料比较全,论文也有,代码库功能完善,确实好用。接着任务一步步清晰,和mentor多次沟通后确定了大体方案。再到自己恍然发现似乎任务和TSP问题高度吻合,也是巧,刚做完非结构化的覆盖中用过TSP进行区间(cell)调度。最后一步步尝试、优化、验证,也算是完整地做出理想的成果了。从被mentor怀疑到认可,再到让我给全组分享,作为新手也稍微有了些信心。
整体方案也没什么了不起,都是基于已有的研究方法。关键在发现问题和抽象问题,把工程应用问题转换为一个已经被广泛研究的问题,也就解决了。
一、Lanelet2地图框架
首先还是按照自己的学习过程,总结一下Lanelet2相关基础,以供自己以后查阅,已经熟悉的读者可以跳过本节。
相关论文:[1] Poggenhans F, Pauls J H, Janosovits J, et al. Lanelet2: A high-definition map framework for the future of automated driving[C]//2018 21st international conference on intelligent transportation systems (ITSC). IEEE, 2018: 1672-1679.
源码链接:GitHub - fzi-forschungszentrum-informatik/Lanelet2: Map handling framework for automated driving
参考资料:
- 论文阅读 | Lanelet2:一种面向未来自动驾驶的高精地图框架
- Lanelet2地图框架代码解析
1.1.概述
- Lanelet2是一个C++库,用于处理在自动驾驶情况下的地图数据。 它兼容并扩展了之前的lanelets库, 能够利用高清地图数据,以有效应对复杂交通情况下车辆所面临的挑战。 灵活性和可扩展性是应对未来地图挑战的一些核心原则。Lanelet2中的地图是自底向上(从定义车道的单个边缘开始,穿过车道到整个街道)定义的,通过与可观察对象相关联来验证地图上的所有信息。
- lanelet2框架下的相关内容在上面给出的论文和源码说明中介绍的十分详细,网上也有许多相关辅助参考。源码中 lanelet2_examples/ 下给出的例程较为详细地说明了增删改查各种元素、地图、路径等等基本操作。
- 本节重点总结与路径覆盖算法相关的内容,如routing模块及相关基础。
1.2.地图格式
Lanelet2格式基于Liblanelet已知的格式,并设计为可在基于XML的OSM数据格式上表示,该格式的编辑器和查看器可公开使用。
OSM—OpenStreetMap是lanelet2软件输出地图的标准格式。
首先,看一下OpenStreetMap的数据结构:
OpenStreetMap的元素(数据基元)主要包括三种:
- 点(Nodes)
- 路(Ways)
- 关系(Relations)
这三种原始构成了整个地图画面。其中,Nodes定义了空间中点的位置;Ways定义了线或区域;Relations(可选的)定义了元素间的关系。示例为源码提供的osm地图mapping_example.osm中的部分:
- Node
node通过经纬度定义了一个地理坐标点。同时,还可以height=标示物体所海拔;通过layer= 和 level=,可以标示物体所在的地图层面与所在建筑物内的层数;通过place= and name=*来表示对象的名称。同时,way也是通过多个点(node)连接成线(面)来构成的。 -
Way
通过2-2000个点(nodes)构成了way。way可表示如下3种图形事物(非闭合线、闭合线、区域)。对于超过2000 nodes的way,可以通过分割来处理。
Open polyline way(非闭合线):收尾不闭合的线段。通常可用于表示现实中的道路、河流、铁路等。
Closed polyline closed way(闭合线):收尾相连的线。例如可以表示现实中的环线地铁。
Area area(区域):闭合区域。通常使用landuse=* 来标示区域等。 - Relation
一个Relation可由一系列nodes, ways 或者其他的relations来组成,相互的关系通过role来定义。一个元素可以在relation中被多次使用,而一个relation可以包含其他的relation。 - Tag
标签不是地图基本元素,但是各元素都通过tag来记录数据信息。通过 ’key’ and 'value’ 来对数据进行记录。
例如,可以通过highway=residential来定义居住区道路;同时,可以使用附加的命名空间来添加附加信息,例如:maxspeed: winter=* 就表示冬天的最高限速。
在JOSM编辑器中可以离线查看和编辑osm地图。
下载地址:JOSM (openstreetmap.de)
相关资料:LearnOSM
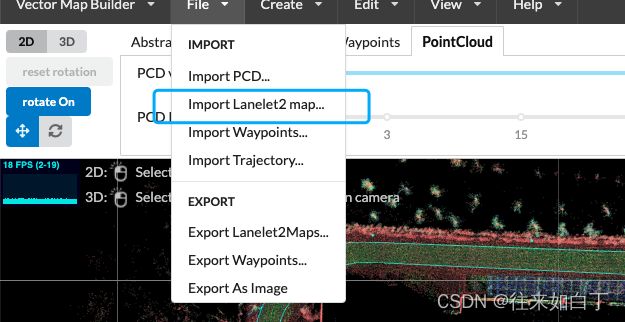
还可以用Autoware Tier4的VectorMapBuilder在网站在线搞。
1.3.Lanelet2地图层次
- 物理层(physical layer,包含真实的,所有可以被观测到的地图元素,比如路面标记、交通灯、路边石头等等)
- 关联层(relational layer,与物理层相关联的车道lanelet,区域area以及交通规则。包含所有对pyhical layer元素的抽象表述,这样所有的地图信息都有道路实体元素承载)
- 拓扑层(topological layer,邻居关系和上下文关系,根据交通参与者road user和道路情况,通过relational layer隐式获取)
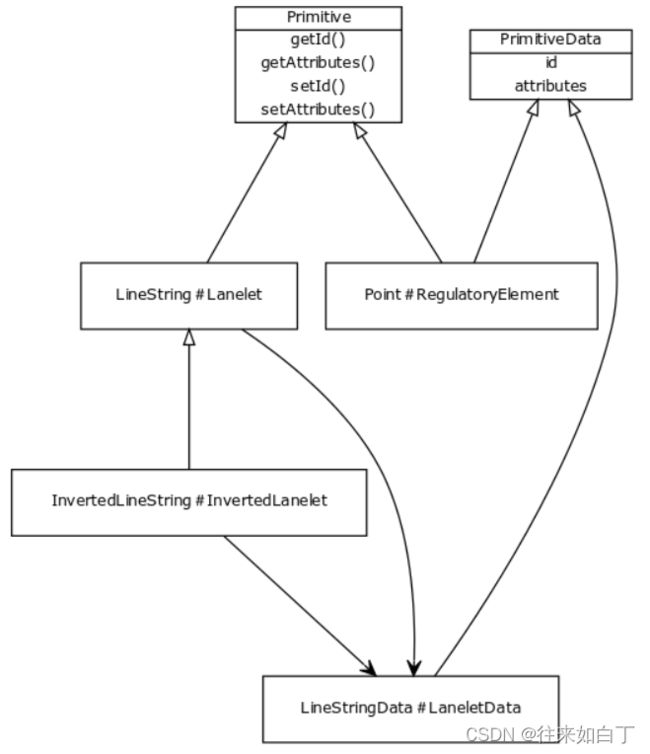
1.4.Primitives-基础元素
上述层级结构主要由六个元素表达:
- Points, linestrings, polygons (physical layer)
- Lanelets, areas, regulatory elements (relational layer)
每个元素的实体都拥有独立的ID号,数据属性通过键值对储存。有些属性是Liblanlet原有的,另外一些是增强地图功能而定义的。
所有基础元素都使用了以下属性:
- type,表示图元所属的类别。例如curbstone,traffic_sign或line_thin用于道路标记。
- subtype,用于进一步区分类型。例如low标记可通行的curbstone,dashed标记虚线道路标记
- no_issue(是/否):如果为yes,则禁止在Lanelet2_validation报告的该图元上发出警告。
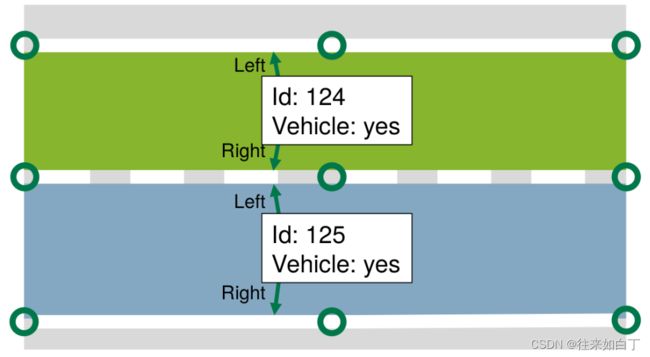
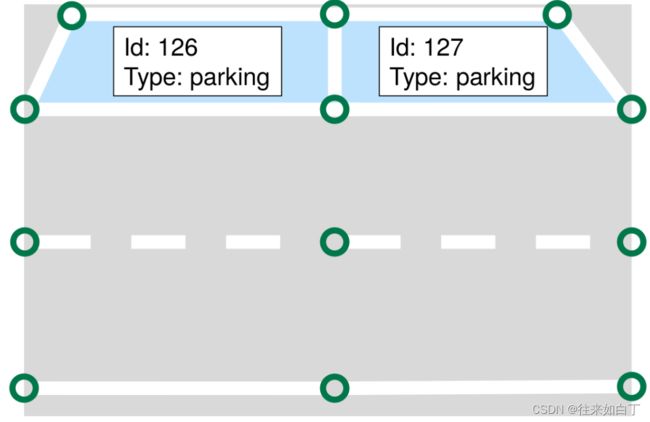
各元素简单示意图如下:
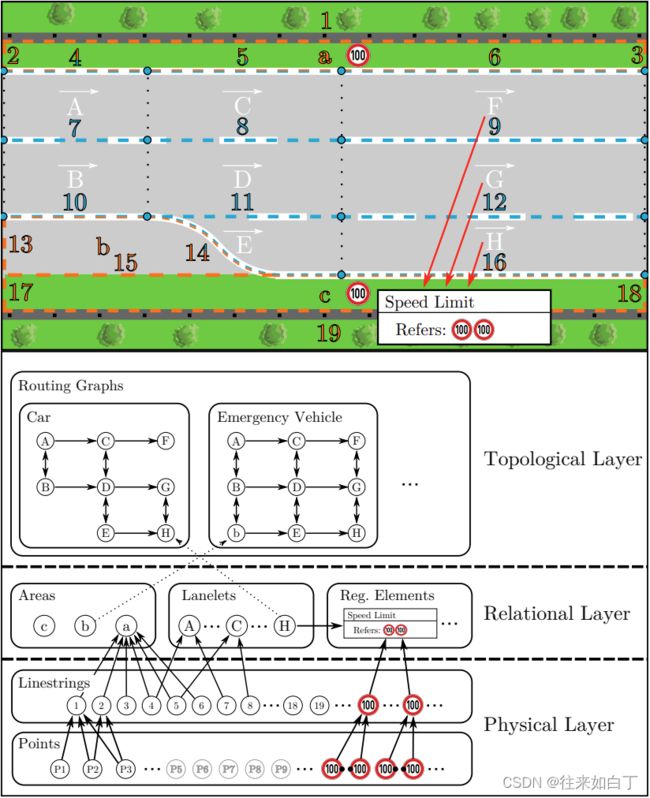
下面是论文[1]中提到的一则综合案例,表达了6个元素与3个图层之间的关系。
Map example for a highway road (enclosed by guardrails) and the resulting map structure. Lanelets have capital letters, areas lowercase letters and linestrings have numbers.
1.5 软件模块(Software Modules)
将地图元素的表示与其解释分开是很重要的,Lanelet2是模块化的,可扩展的软件框架,其软件框架主要分为以下模块。
- Core
此模块包含所有的图元和以上描述的图层,并且还包括几何计算,比如计算中心线,距离和重叠区域等 - Traffic Rules
根据不同的road user类型和国家,来解释相应的交通规则。 - Physical
可以直接访问物理层元素。 - Routing
根据交通规则,创建路由图,来确定精准的行驶路线。也可能通过组合相邻的Areas和lanelets来构建易通行区域。 - Matching
用来给road user分配lanelets或者基于传感器的观测来确定可能的行驶方向。 - Projection
提供全球地理坐标系到局部平面坐标系的准换 - IO
用于从各种地图格式(特别是OSM格式)读取和写入地图。 -
Validity
搜索和报告地图中的显著错误
二、Lanelet2的routing模块
接下来,介绍使用Lanelet2时最重要的模块routing。这是组成拓扑层,并实现相关图搜索寻路算法的模块。也是抽象问题的第一步:结构化道路按交规抽象为拓扑图。
原作者相关论文:[2] Poggenhans F, Janosovits J. Pathfinding and Routing for Automated Driving in the Lanelet2 Map Framework[C]//2020 IEEE 23rd International Conference on Intelligent Transportation Systems (ITSC). IEEE, 2020: 1-7.
——得益于lanelet自底向上的设计理念,关键的一步是理解Lanelet2 map并不是显式的routing图。要将Lanelet2地图转换为图形,必须对其进行解释(interpreted)。这种解释取决于上下文。图形总是满足某个特定的功能,因此它只对某个road user或某个国家有效。
2.1 论文总结
《Pathfinding and Routing for Automated Driving in the Lanelet2 Map Framework》
2.1.0 摘要
在本文中,我们介绍了路由 routing 和寻路 pathfinding 的概念,它被Lanelet2地图框架用于自动驾驶。在传统的map框架中,路由图routing graph是明确预定义的,而Lanelet2在运行时对其进行解释。
这允许从不同角度查看地图信息,例如其他道路用户或其他交通状况。我们还分析了自动驾驶中的路由routing应用中通常需要哪些信息,这如何影响路由图的形状,以及如何有效地提取这些信息。
2.1.1 为什么要考虑寻路Pathfinding问题
查找路线的一种有效方法是将地图map视为图形graph,并使用图搜索方法进行搜索。但在自动驾驶的背景下,routing不仅仅意味着找到从A到B的最佳路线。对于车辆,还意味着以超车机动的形式自发地规划可供选择的路径,以及能够在转弯机动之前及时启动车道变换。自动驾驶不仅与自身车辆有关,也与其他road user有关。因此需要了解其他道路使用者有哪些可允许的选择,并认识到他们的意图,以便在确定车辆行为时考虑到他们。
为了能够执行这些操作,道路结构的模型需要足够通用,以描述各种各样的道路场景。更应当足够灵活、简单易懂、安全、避免出错。
因此文章接下来介绍了我们认为应该如何设计适合自动驾驶的路线图routing graph。在此基础上,现在可以从路由图的角度更精确地定义重要术语,如可达集reachable sets和路线route,从而确保地图和运动规划之间有意义且有统一的接口。
2.2.2 Lanelet2如何工作
Lanelet2世界不是自上而下建模的(从整条街道到单独的车道及其边界),而是自下而上建模的(从定义车道的单独边缘开始,穿过车道到整个街道)。
Lanelet2的基本构造块是Lanelet,这是一种发生定向运动的通用车道。此外将Area用作发生无向运动的路段。可以为Lanelets和Areas分配属性和交通规则,以便为本路段的道路使用者提供相关信息。
需要导航的世界全部由这些Lanelets和Areas组成,这些Lanelets和Areas通常只有几米长,因此可以以高计算效率的方式进行处理。
2.2.3 其他map框架如何表示routing information
以OpenDrive为例,它将世界划分为道路roads和路口junctions。对于每一条道路和交叉口,它都明确地存储了其后续或前驱的一条道路,从而在道路级别定义了路线图。这必须为每条道路提供额外的属性。一条道路沿纵向分为几个路段,然后沿横向分为几个车道。车道的位置并不明确,它被指定为与道路参照线(通常是样条曲线)的横向偏移。为了指示连续道路的哪些车道相互连接,必须指定车道连接记录lane link record。
劣势:
- 这种建模需要大量冗余信息,因此对错误的敏感性很高。
- 在车道级别上布线要复杂得多,因为车道没有明确存储。
- 很难包含其他道路使用者的信息
2.2.4 一个 Lanelet2 Map 并不是一个 Graph
如何通过使用像Lanelet2这样的自下而上的方法更好地解决这个问题?关键的一步是理解Lanelet2 map并不是显式的路由图。事实上,你甚至不能说它隐含着一个graph。要将Lanelet2地图转换为graph,必须对其进行解释(interpreted)。这种解释取决于语境。一个graph总是满足某个特定的功能,因此它只对某个道路使用者或某个国家有效。map与创建routing graph的不同交通规则之间的连接关系:
创建Lanelet2地图时,无需指定邻里关系。它们直接源于相邻的Lanelets和Area使用相同的点或线串。因此地图总是一致的。
只有在需要确定的graph时,才会根据邻里关系的类型在车道级别创建graph。因此,Lanelet和Areas构成了graph的顶点。
对于要成为图中顶点的Lanelet或Area,它必须在创建graph的上下文中是可通过的(passable)。这些顶点之间的边有七种不同的关系:following, (adjacent) left, (adjacent) right, area, and conflicting:
-
Lanelet B is following Lanelet A:如果两者都是passable的,它们在几何上是连续的(即A的左右边界的最后一点与B的第一点相同),并且如果允许从A移动到B(必须按此顺序)。
-
如果Lanelet A的右边界与Lanelet B的左边界相同,且两者都可以通行,并且如果允许在该边界上的这一点上改变车道,则B is left from A;
如果不允许改变,则B is adjacent left from A. -
这一类比适用于right和adjacent right的右边界。A和B之间的这种关系只是部分对称。例如,允许车道从A变为B,但不允许从B变为a。因此,从A到B的关系为“left”,但从B到A为“adjacent right”。
-
如果一个Area与一个Lanelet共享其边缘的一部分,这两个区域都是可通行的,并且允许它从一个区域移动到另一个区域,则关系为Area。
-
如果两个Lanelet或Area重叠,则它们的关系为conflicting。与上述其他关系不同,只有其中一个区域是passable的,此边才能存在于graph中。
可以看出,除了纯粹的几何条件外,四个不同的标准足以确定routing map,这些确定routing graph的属性称为其 traffic rules。
- 一个Lanelet/Areas是否可以通行
- 是否允许从一个Lanelet到另一个Lanelet行驶
- 两个Lanelets之间是否允许换车道
- 是否允许在相邻Areas和/或Lanelets之间切换
2.2.5 到底什么是一条 Route
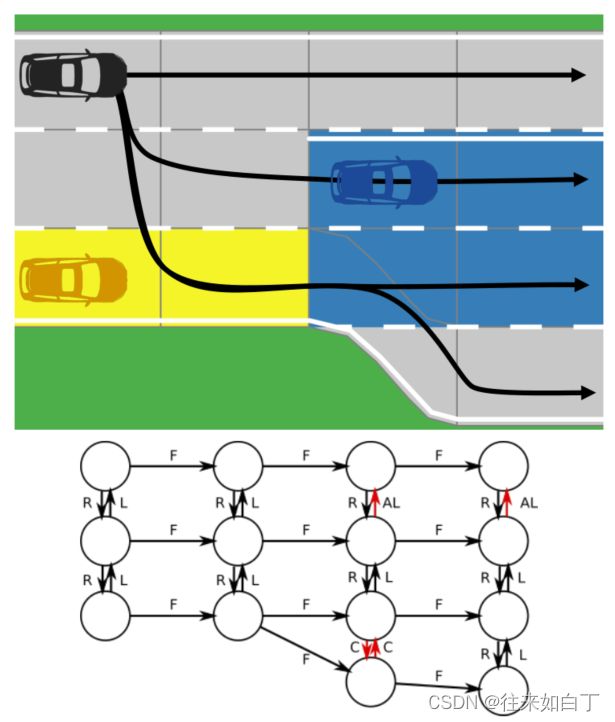
Fig. 2: Example of a reachable set (blue), a lane (yellow), and possible paths (black arrows).
Below: Underlying graph with following (F), left (L), adjacent left (AL), right (R), and conflicting (C) edges. Non-drivable edges are red.
检查下列术语,并根据Lanelets和Area找到合适的定义,以满足自身的运动规划和对其他人的预测要求。
-
Path, Lanelet Sequence and Lane
通常,Path指道路使用者行驶或希望行驶的连续路段。我们假设一条Path始终是连贯的,并且与交通规则一致。这意味着它还可以包括车道更改。道路使用者也可使用Areas到达目的地。
因此,Lanelet2的Path定义如下:道路使用者可驾驶的Lanelets和Area的有序序列,在相应的路线图中,每两个连续Lanelets之间存在“following”、“Area”、“left”或“right”关系。如果不允许“区域”关系(即定向驾驶),则为Lanelet序列。例如,图2中黑色车辆的每条线是一个Lanelet序列(也是一条路径)。
如果不允许更改车道,则为“lane”。例如,图2中的黄色区域形成一条车道。
- Reachable Set and Possible paths
在Lanelet2中,可达集是道路使用者在特定情况下可以到达且不超过cost限制的所有Lanelet和Area的集合。与前面的术语不同,给定图中的可达集只有与特定的cost函数结合时才有意义。它通常用于确定用户在给定时间内可以到达的区域。
possible paths是道路使用者在一定成本限制内可以选择的所有Path的集合,以便通过其最佳路径到达每个车道或区域。例如,对于图2所示的黑色车辆,possible paths是图2所示的Paths。
- Route
已知一条轨迹后,可以使用Lanelet到达目的地而不必离开该轨迹的所有Lanelet的集合。
假设最初已知一个可行驶的Lanelet序列,它连接起点和终点。这是route的一部分。以下每一个Lanelet sequence也属于该route,如果该序列:
- 不包含已经是route一部分的Lanelet
- route中有一个Lanelet,序列的第一个Lanelet与之是“跟随”、“左”或“右”的关系
- route中有一个Lanelet,序列的最后一个Lanelet与之是“跟随”、“左”或“右”的关系
-
序列中的每个Lanelet与路线中的至少一个Lanelet具有“adjacent left”、 “adjacent right”或“conflicting”关系,这些Lanelets依次形成一个序列。
作为示例,该定义的结果如图3所示。
一般来说,当添加新车道时,分支车道也是route的一部分(如图3a所示),因为即使它们在短时间内没有左右邻居(邻居是路线的一部分),它们仍然与路线的其余部分(以及与它们相关的路线)存在“conflicting”。
当Lanelets离开routing时,情况就不同了,如图3b所示。在这种情况下,中间Lanelet与route不接触,因此分支Lanelet、中间Lanelet和合并Lanelet组成的整个序列不能成为route的一部分。
特殊情况如图3c所示。此处,中间的分支和合并Lanelets始终与route接触,但route并非始终与Lanelets接触(尤其是右侧曲线中的Lanelet)。因此,它们不能成为route的一部分。
Fig. 3: Multiple examples of a route with the given input Lanelet sequence in yellow and the resulting route highlighted in blue. Grey lines mark lanelet boundaries.
应该注意的是,Lanelets的确切划分位置确实很重要。如果Lanelets太大,结果可能会不同。例如,如果图3c右侧曲线中的三个Lanelets只有一个(???),它将首先从中间的曲线分支出来,然后分离,最后再次合并。
2.2.6 最优路径是一个视角问题
为了在图中执行搜索,通常不仅需要图的拓扑,还需要costs。毕竟,寻找路线的过程通常与某种优化需求有关,比如尽快到达目的地。
确定最佳路径的标准也取决于上下文。在自动驾驶中,不只关注全局最优路径,通常对局部最优路径也感兴趣。costs criteria可能因道路使用者而异。因此,在Lanelet2中,每个edge都关联了多个cost标准,因此在驾驶过程中可以根据需要使用不同的cost标准。
对于自动车辆来说,车道变换始终是一个挑战,因为很难预测其他道路使用者的行为,安全性无法始终得到保证。因此,通常希望找到能为车道变更留出尽可能多时间的路线,并且通常更喜欢车道变更发生得更早的路径。因此,车道变更cost应单独计算。
具体如下:
对于有“following”关系的两个Lanelets,cost只是关于这两个Lanelets的函数:
对于有“left”和“right”关系的n个Lanelets,costs是关于可用于车道变换的所有n条Lanelets的函数:
ff 的定义通常是,车道的剩余长度减少,cost就增加。由于车道变更的可用距离越来越短,剩余的Lanelets就越少,因此及时的车道变更被优先考虑。
2.2.7 自动驾驶不仅仅是”驾驶“
沿道路的定向运动只是一种可能的驾驶条件,尽管是最常见的。我们想更详细地了解我们所说的驾驶的确切含义,以及我们认为它如何影响对地图的要求。
在Parking时的无方向运动,与单独车道的行驶方向是不相关的,只是在有限的区域内到达目的地,如有必要,在不妨碍其他道路使用者的情况下倒车。关于Lanelet2中的表示,这意味着如果可以使用Area,也可以使用Area。也可以使用其他车道的车道,但应避免使用,以免妨碍其他道路使用者。在其他地图格式中需要对每个单独情况明确规定。在Lanelet2中,它只需要更改交通规则(在Lanelet2定义中的),根据这些规则在路由图中的Lanelets和Area之间创建edge。这些定义的具体方式因国家和车辆而异。
文献中经常讨论个别道路使用者不遵守交通规则时可能发生的情况。大多认为在这种情况下,地图毫无价值,因为原则上任何运动都是可能的。但并非如此,因为可能的运动仍然受到物理障碍物和道路几何形状的限制。即使在这种情况下,车辆的可达范围也是有限的。对于自身车辆,交通规则排在第二位的情况也存在,例如当传感器发生故障时将要到达安全状态。
这些案例研究表明,路线图强烈依赖于道路使用者的意图。但其实质是,第四节中提出的交通规则只需要以不同的方式定义,足以涵盖这些情况。重要的观察结果是,无论交通规则是如何定义的,从图中可以获得的与车辆相关的最终结果通常仍然是一个可达集、可能的路径或路线。
2.2.8 不是所有东西都是车
传统地图格式的另一个典型问题是,它们通常只从特定road user的角度传达有关道路的信息。其他road user所需的任何信息只有在被认为与该特定road user“相关”时才会被存储。
但实际上很难确定一条信息何时是不相关的。研究表明,如果还知道行人有哪些其他选择(例如继续在人行道上行走),则更容易预测行人是否会进入街道。还有其他原因可以解释为什么绘制道路以外区域的地图是有用的,比如用于车辆定位、检查传感器信息的合理性,甚至用于转弯和停车等更不寻常的驾驶动作。如果其他车辆在“正常”驾驶过程中的行为与预期不符,这些信息可能有利于自身车辆正确区分其他车辆的意图。
因此,将所有具有相关特征的区域纳入自动车辆可以观察到的地图中,是更好的方法。由于有更多的上下文信息,可以更容易地检查存储的地图信息的合理性,并避免丢失重要信息。
主要优势在于这种地图构建令信息呈现更加同质。如上第七节所述,从该路线图中得出的信息表示形式不变。一个可到达的集合或路线对行人和车辆都同样有意义
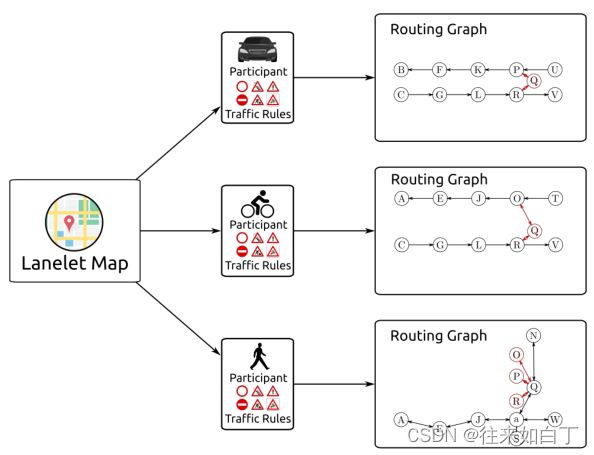
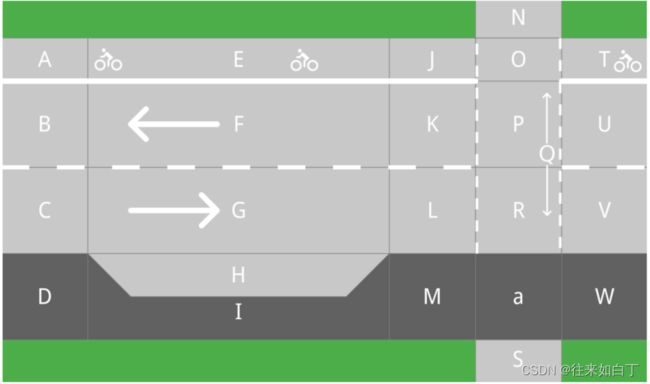
例如,参考图4。对于a区的行人,可达集包含所有可用选项:使用Lanelet M和W继续在人行道上行走;或使用Lanelet Q横穿道路,或沿着人行道S行走。了解这些选项对于理解行人的意图非常有帮助,可以将其与行人观察到的视觉线索结合起来。
Fig. 4: Example scene with Lanelets (capital letters) and Areas (small letters). Resulting routing graphs can be seen in Fig. 1.
Fig. 4 Fig.1
2.2 example中Routing部分涉及用法简介
代码位于 lanelet2_example/src/06_routing/main.cpp
本节主要总结如何根据加载的地图,创建和使用路由图。从map,交规,routing cost中可以得到路由图。路由代价主要是根据距离和时间(限速信息)综合计算,路由图可用于查询三种不同的信息:
- 特定Lanelet/Area的相邻关系
- 来自Lanelet/Area的可能通行的路线
- 两个Lanelet之间的最短路线。
该示例包含三个部分:
-
part1CreatingAndUsingRoutingGraphs();
-
part2UsingRoutes();
-
part3UsingRoutingGraphContainers();
| 模块 | 输入 | 输出 | 功能 | |
|
||||
| 获取lanelets的邻居关系 | routing::RoutingGraph::build |
const LaneletMap& laneletMap const traffic_rules::TrafficRules& trafficRules RoutingCostId routingCostId |
routing::RoutingGraphUPtr routingGraph |
创建生成路由图 |
| routingGraph::adjacentLeft routingGraph::adjacentRight |
const ConstLanelet& lanelet RoutingCostId routingCostId |
Optional |
查询当前车道的一些相邻车道 |
|
| routingGraph::left routingGraph::right |
const ConstLanelet& lanelet RoutingCostId routingCostId |
Optional |
查询当前车道的一些"left", "right"车道 |
|
| RoutingGraph::besides |
const ConstLanelet& lanelet RoutingCostId routingCostId |
ConstLanelets |
查询当前车道所在road的slice |
|
| RoutingGraph::following |
const ConstLanelet& lanelet bool withLaneChanges |
ConstLanelets |
查询当前车道的一些"following"车道 | |
| const ConstLaneletOrArea& laneletOrArea |
RoutingGraph::conflicting |
ConstLaneletOrAreas |
查询当前车道的一些"conflicting"车道或区域 | |
| 找到与生成route相关的possible path、可达集等 | RoutingGraph::possiblePaths |
const ConstLanelet& startPoint double minRoutingCost RoutingCostId routingCostId bool allowLaneChanges |
LaneletPaths |
搜索代价为x,并且距离当前位置minRoutingCost米的路线,allowLaneChanges表示是否允许变道 |
| RoutingGraph::reachableSet |
const ConstLanelet& lanelet double maxRoutingCost RoutingCostId routingCostId bool allowLaneChanges |
ConstLanelets |
获取所有的可达路线集合,该集与可能路径集合基本相同,但是lanlet未排序,不包含重复项。 同时可能路径集合会丢弃低于成本阈值的路径,而可达集合会保留所有路径。 |
|
| RoutingGraph::shortestPath |
const ConstLanelet& from const ConstLanelet& to RoutingCostId routingCostId bool withLaneChanges |
Optional |
获取最短路径。与其说它是一条完整路线的建议,不如说是一条指导车辆选择哪个车道的指南。 | |
| LaneletPath::getRemainingLane |
LaneletPath::const_iterator laneletPosition |
LaneletSequence |
是上个函数输出LaneletPath对象的成员函数,获取剩余车道。您可以查找可以遵循的Lanelet序列的路径,直到必须进行车道更改为止 |
|
|
||||
| 对Route类的相关操作 | RoutingGraph::getRoute |
const ConstLanelet& from const ConstLanelet& to RoutingCostId routingCostId bool withLaneChanges |
Optional |
获取从from到to的路径。Route对象建立在起点和终点之间的最短路径上。 但是,它不仅包含沿最短路径的lanelets,还包含可以到达目的地而无需离开所选道路的所有lanelets。 当需要知道到达目的地的所有选项(包括变道)时,可以使用。 |
| Route::shortestPath |
无 | const LaneletPath& |
routing::Route的成员函数。基于当前的Route返回最短路径Path |
|
| Route::fullLane |
const ConstLanelet& ll |
LaneletSequence |
现在我们可以从路线中获得单独的车道。 在到达目的地或我们必须改变车道之前,它们尽可能长 | |
| Route::rightRelation |
const ConstLanelet& lanelet |
Optional |
但我们也可以检查更早的变道可能性或查询其他关系,类似于路由图。 | |
| Route::laneletSubmap |
无 | LaneletSubmapConstPtr |
根据只包含相关元素的路线创建一个lanelet子图 | |
|
||||
| 在不同road users构成的多个routing graph中查找冲突 | RoutingGraphContainer::RoutingGraphContainer |
std::vector |
RoutingGraphContainer的构造函数 | |
| RoutingGraphContainer::conflictingInGraph |
const ConstLanelet& lanelet size_t routingGraphId double participantHeight = .0 |
ConstLanelets |
在指定图中查找与给定lanelet冲突的lanelets | |
| RoutingGraphContainer::conflictingInGraphs |
const ConstLanelet& lanelet double participantHeight = .0 |
ConflictingInGraphs |
在所有图中查找与给定lanelet冲突的lanelets | |
3. 基于Lanelet2的覆盖算法
最后,抽象问题并详述解决思路。
算法整体思路:
- 将经过一个lanelet定义为完成对其的覆盖,因此直接生成由lanelet序列组成的path
- 每条path(或每个lanelet)有对应的分类标签:left、center、right,分别表示在该lanelet中靠左、中、右行驶,传递给下游planning。
- 按一定顺序依次把所有lanelet加入路径path,并保证效率。
注:实际清扫时可能需要每个lanelet清扫(经过)不止一遍(即根据实际宽度,扫左、中、右),本算法只要求每个lanelet至少经过一次。
3.1 按DFS顺序清扫
按深度优先搜索的顺序把所有lanelet加入路径path:
按照以下流程
1.定义Close表、一个存储搜索顺序的栈stk、存储路径的数组path
2.start_lanelet加入stk
3.
while(!stk.empty()){
当前所在的位置 pose = path.back();
当前搜索到的lanelet cur = stk.top();
stk.pop();
if(cur not in Close){
if (pose != cur) {
规划pose到cur的路径并加入path,且把途径的lanelet加入Close表
}
for(cur的所有following Lanelet){
stk.push(following);
}
cur插入Close表;
path.push_back(cur);
}
}
4.规划从path.back()到goal_lanelet的路径并加入path3.2 抽象为ATSP(非对称旅行商问题)求解清扫顺序
3.2.1 ATSP问题简介
旅行商问题(Travelling salesman problem, TSP)是组合优化中的一个NP困难问题,问题内容为“给定一系列城市和每对城市之间的距离,求解访问每一座城市一次并回到起始城市的最短回路。“
可以用无向加权图来对TSP建模,则城市是图的顶点,道路是图的边,道路的距离就是该边的长度。它是起点和终点都在一个特定顶点,访问每个顶点恰好一次的最小化问题。
- 非对称和对称
在对称TSP问题中,两座城市之间来回的距离是相等的,形成一个无向图。这种对称性将解的数量减少了一半。在非对称TSP问题中,可能不是双向的路径都存在,或是来回的距离不同,形成了有向图。交通事故、单行道和出发与到达某些城市机票价格不同等都是打破这种对称性的例子。
from:旅行推销员问题 - 维基百科,自由的百科全书 (wikipedia.org)
3.2.2 与覆盖算法建立联系
- ATSP问题可以建模为加权有向完全图
- 基于交规和参与者可以生成lanelet2的routing graph,这可以视为一个加权有向图:lanelet表示为点,lanelet之间的关系表示为边。各边权重可以用cost表示。
cost默认有两种计算方式:costId == 0,基于lanelet长度;costId == 1,基于最大限速的行驶时间。默认costId为0。 - 任意两点间需要有加权边,图中的各边用邻接矩阵描述。
在routing graph中任意两个lanelet要么有直接的relation,要么有最短路径相连。如果原graph中不存在从一个lanelet A到另一个lanlet B的边,就需要调用shortestPath函数得到路径,再把途径的边的cost累加,作为A到B的边的权值。 - 重要区别:Hamilton圈与Hamilton路径
Hamilton圈:给定一个有向图G(V,E),如果G中的圈C恰好经过每一个顶点一次,则称圈C是一个哈密顿圈。
Hamilton路径:图的一条路,经过每个顶点恰好一次。
注:在一条哈密顿路的基础上,再有一条边将其首尾连接,所构成的圈。注意,若有一个哈密顿圈,则移除其任一条边,皆可得到一条哈密顿路,但反之则不然,即给定一条哈密顿路,不一定能延伸成哈密顿圈,因为该路径的首尾两顶点之间,不一定有边相连。
ATSP问题是求出了Hamilton圈,而路径覆盖算法不要求路径最后回到起点,因此求得的是一条Hamilton路径。
于是设置一个虚节点来处理:
如下图加入虚节点E,该点与其他所有节点的边权值皆为0。基于新图求解得到的最短Hamilton圈,去掉虚节点及其相关边,就是最短Hamilton路径了。
简单理解就是,假设经过虚节点可以跨过原图任意一条边,那么新图的最短Hamilton圈(ATSP问题的近似最优解)就可跨过(去掉)原图最长的边,构成原图的最短Hamilton路径。
综上,获得graph的邻接矩阵后,就可以求解ATSP问题,得到总cost最小的覆盖路径。
3.2.3 求解方案
常用方法:
- 动态规划,Branch & Bound——krplata/tsp: Asymmetric Travelling Salesman Problem exact solution algorithms. (github.com)
- 遗传算法——基于遗传算法(Genetic Algorithm)的TSP问题求解(C) - 游-游 - 博客园 (cnblogs.com)
求解器:
- Concorde——Concorde README and Installation guide (uwaterloo.ca)
- Cplex
- LKH——LKH-3 (Keld Helsgaun) (ruc.dk)
经过调研和实验,选用LKH-3作为求解器,LKH是当前公认求解tsp最好的算法,基于Lin-Kernighan思想,通过将图上的连接边切断、重连的方式(2-opt, 3-opt...)一次次改进获得更好的路径解。交换边的数量越多得到的解质量越好。其求解结果与TSPLIB标准数据集基本一致!
按上述LKH-3网站下载编译后找到可执行文件,在本项目源代码planning/mission_planning/mission_planner/src/mission_planner_lanelet2/TSP_LKH.cpp中通过LKHTSPSolver::solveLKHTSP函数的cmd变量生成命令行进行调用,因此应该保证项目运行的路径中有LKH可执行文件,源码中./LKH 一般表示当前文件夹位于home/.ros/,因此把LKH复制到该文件夹就可运行(仅就我的ros-kinetic版本)。
另外LKH本身采用命令行调用,非常简单,具体可直接Google。注意代码中在运行配置文件.par中设置了输出文件ATSP_output.txt,以便保存和读取结果。
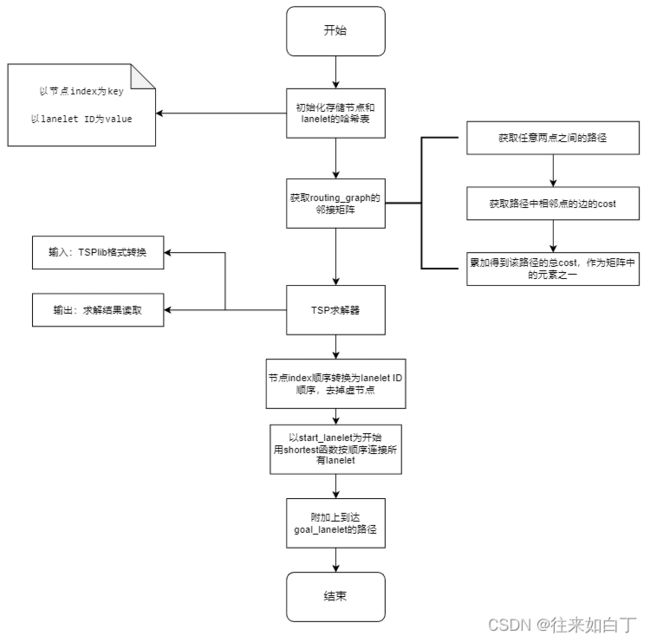
3.2.4 算法流程
代码运行流程如下:
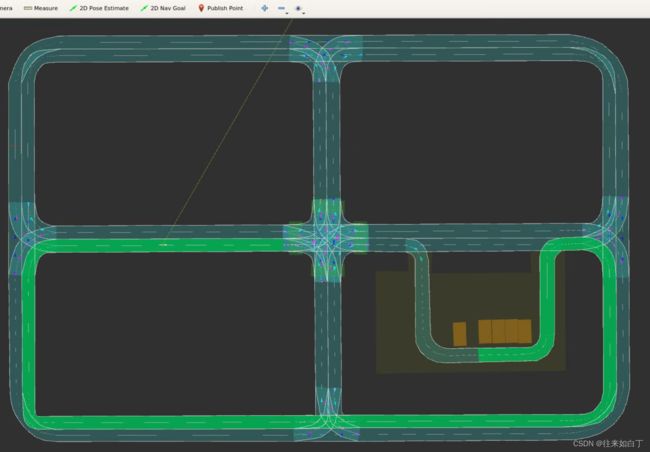
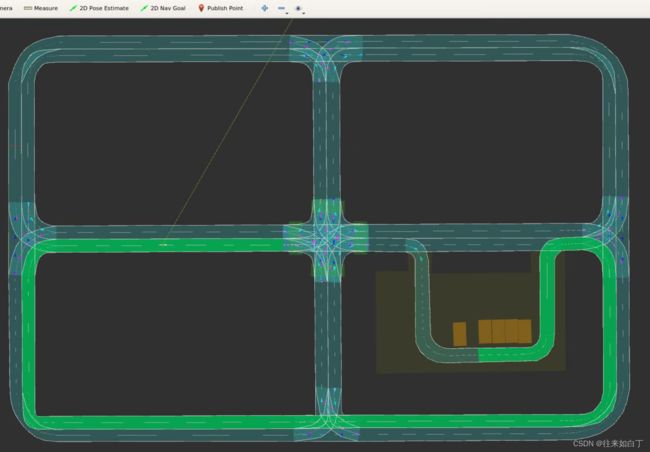
3.3 运行Demo和效果
| 方案 |
地图 |
路径lanelet数量 |
路径长度(m) |
覆盖率 |
覆盖效率 |
耗时 |
理论最优解 |
运行信息 |
演示视频 |
|---|---|---|---|---|---|---|---|---|---|
| 深度优先搜索 |
201 | 5022.72 | 100% | 39.3%(lanelet数量) 34.0%(Length) |
0.001s | --- |
结构化路径DFS覆盖算法演示 |
||
| ATSP | 149 | 3649.79 | 100% | 53.0%(lanelet数量) 46.8%(Length) |
0.1s左右 |
3252.86 |
结构化路径ATSP覆盖算法演示 |
||
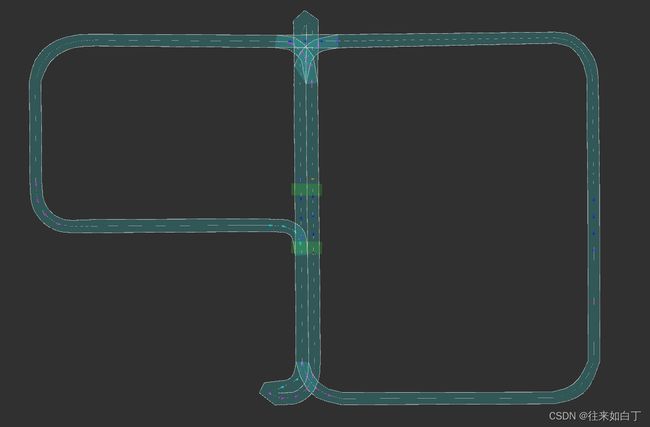
| ATSP | 36 | 811.855m | 100% | 75.0%(lanelet数量) 77.8%(Length) |
0.008252s | 811.855m |
simple结构化路径ATSP覆盖demo |
4. Lanelet2的routing过程可视化
项目代码base一个简易的基于Lanelet2手动选定起始、目标生成可视化最短路径的教学
参考链接:
GitHub - AbangLZU/ad_with_lanelet2: sample of ad system to use lanelet2 framework
面向自动驾驶的高精度地图框架解析和实战
ad_with_lanelet2 编译问题解决
注意安装 unique-id
sudo apt-get install ros-kinetic-unique-id
通过rviz给定的起始lanelet和目标lanelet,利用routing函数实时生成可行路径并显示。在此基础上修改了lanelet话题发送、rviz显示颜色、更新频率等,以及重新写了规划路径的函数。并用 iter4的工具制造一个更简易的地图。
后记
从打算转到路径规划方面以来,这是自己第一个上手从调研到提出想法,再到实现、优化的“项目”。实习确实给了自己一些尝试的机会,了解了真正要落地的项目开发的流程、协作的过程,各种开发工具,各个大会小会,对比下来,学校的所谓“项目”真是过于理想化和不成熟了。
在进行这个项目的时候自己真是全心投入,也乐在其中,虽然没有什么创新的算法提出,但能亲自解决一个实际问题的感觉还是很不错的。也许也看清了自己对工程实现更感兴趣。慢慢学习积累吧,希望自己也能提出“新东西”。
只是有些迷茫和彷徨,我明明想入行自动驾驶,怎么做了三个月的清扫车呢?唉~但愿有用