数据结构与算法学习⑤(BFS和DFS 贪心算法 二分查找)
数据结构与算法学习⑤
- 数据结构与算法学习⑤
-
- 1、BFS和DFS
-
- 1.1、深度优先搜索算法
- 1.2、广度优先搜索算法
- 面试实战
-
- 102. 二叉树的层序遍历
- 104. 二叉树的最大深度
- 515. 在每个树行中找最大值
- 200. 岛屿数量
- 2、贪心算法
-
- 322. 零钱兑换
- 面试实战
-
- 455. 分发饼干
- 122. 买卖股票的最佳时机 II
- 55. 跳跃游戏
- 45. 跳跃游戏 II
- 860. 柠檬水找零
- 3、二分查找
-
- 3.1原理分析
- 3.2、复杂度分析
- 1.3、代码实现
- 1.4、应用场景说明
- 34. 在排序数组中查找元素的第一个和最后一个位置
- 74. 搜索二维矩阵
- 2、面试实战
-
- 69. x 的平方根
- 33. 搜索旋转排序数组
- 153. 寻找旋转排序数组中的最小值
- 74. 搜索二维矩阵
数据结构与算法学习⑤
1、BFS和DFS
深度优先搜索算法(DFS)和广度优先搜索算法(BFS)是一种用于遍历或搜索树或图的算法,在搜索遍历的过程中保证每个节点(顶点)访问一次且仅访问一次,按照节点(顶点)访问顺序的不同分为深度优先和广度优先。
1.1、深度优先搜索算法
深度优先搜索算法(Depth-First-Search,DFS)沿着树的深度遍历树的节点,尽可能深的搜索树的分支。当节点v的所在边都己被探寻过,搜索将回溯到发现节点v的那条边的起始节点。这一过程一直进行到已发现从源节点可达的所有节点为止。如果还存在未被发现的节点,则选择其中一个作为源节点并重复以上过程,整个进程反复进行直到所有节点都被访问为止。属于盲目搜索。
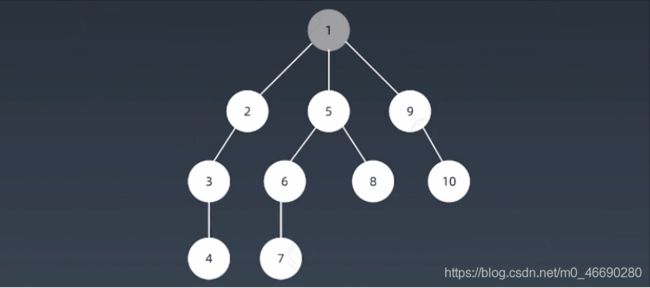
注意:
1:实际上,回溯算法思想就是借助于深度优先搜索来实现的。
DFS负责搜索所有的路径,回溯辅以选择和撤销选择这种思想寻找可能的解,当然代码写起来基于递归(所以代码写起来就是用递归实现的)。
2:DFS跟回溯有什么关系呢?
回溯是一种通用的算法,把问题分步解决,在每一步都试验所有的可能,当发现已经找到一种方式或者目前这种方式不可能是结果的时候,退回上一步继续尝试其他可能(有一个选择和撤销选择的过程,可理解为标记访问和删除访问标记)。很多时候每一步的处理都是一致的,这时候用递归来实现就很自然。
**当回溯(递归)用于树(图)的时候,就是深度优先搜索。**当然了,几乎所有可以用回溯解决的问题都可以表示为树。(像之前的排列,组合等问题,虽不是直接在树上操作,但是他们操作的中间状态其实是一棵树)那么这俩在这里就几乎同义了。如果一个问题解决的时候显式地使用了树或图,那么我们就叫它dfs。很多时候没有用树我们也管它叫dfs严格地说是不对的,但是dfs比回溯打字的时候好输入。
DFS代码参考模板:
private void dfs(TreeNode root,int level,List<List<Integer>>results){
//terminal
if(results.size()==level){ //or root==null or node alread vistited
results.add(new ArrayList<>());
return;
}
//process current level node here
results.get(level).add(root.val);//记录当前节点已被访问
//drill down if node not vistited
if(root.left!=null){
dfs(root.left,level+1,results);
}
if(root.right!=null){
dfs(root.right,level+1,results);
}
}
是不是觉得跟二叉树的前中后序遍历很像,其实二叉树的前中后序遍历就是一种DFS,只不过记录节点的时机不一样而已。
针对多叉树的DFS,代码参考模板如下:
public void dfs(Node node,List<Integer> res) {
//terminal
if (node == null) {
return;
}
//process current level logic
res.add(node.val);
//drill down
List<Node> children = node.children;
for (Node n:children) {
// if node not visited then dfs node
if (not visited) {
// 在基于图的dfs中一般需要判断顶点是否已访问过
dfs(n,res);
}
}
当然我们也可以自己使用栈来模拟递归的过程,将递归代码改写成非递归代码!
针对图的深度优先搜索算法,思路是一致的
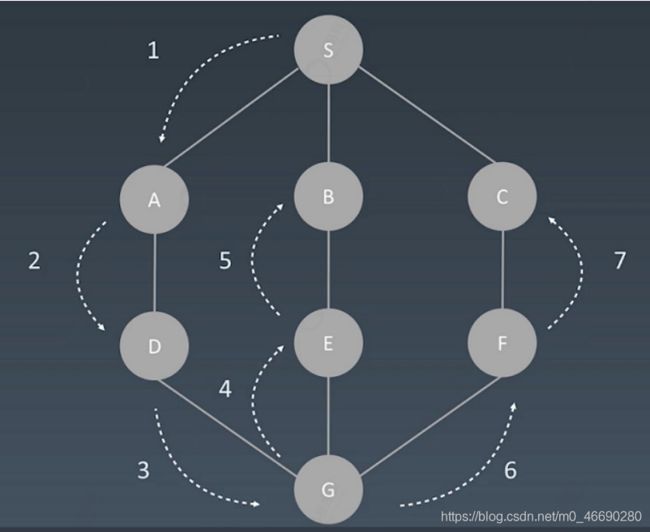
假设:从S开始进行查找,每次查找,先一头扎到底,然后再回退,回退过程中有别的路再一头扎到底。
比如:S->A->D->G->E->B,到底了,然后回退到G,再一头扎到底,S->A->D->G->F->C
1.2、广度优先搜索算法
广度优先搜索算法(Breadth-First-Search,BFS)直观地讲,它其实就是一种“地毯式”层层推进的搜索策略,即先查找离起始顶点最近的,然后是次近的,依次往外搜索。
简单的说,BFS是从根节点开始,沿着树(图)的宽度遍历树(图)的节点。如果所有节点均被访问,则算法中止,一般用队列数据结构来辅助实现BFS算法。
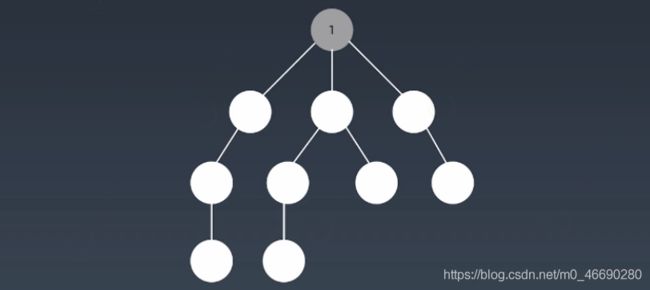
就像在湖面上滴一滴水,形成的水波纹!向四周散开
dfs和bfs搜索方式的比较:

BFS代码的参考模板:需要借助一个队列Queue(或Deque)
public class TreeNode {
int val;
TreeNode left;
TreeNode right;
TreeNode(int x) {
val = x;
}
}
public List<List<Integer>> levelOrder(TreeNode root) {
List<List<Integer>> allResults = new ArrayList<>();
if (root == null) {
return allResults;
}
Queue<TreeNode> nodes = new LinkedList<>();
//将根节点入队列
nodes.add(root);
while (!nodes.isEmpty()) {
//每次循环开始时:队列中的元素的个数其实就是当前这一层节点的个数
int size = nodes.size();
List<Integer> results = new ArrayList<>();
for (int i = 0; i < size; i++) {
//从队列中取出每一个节点(取出这一层的每个节点)
TreeNode node = nodes.poll();
results.add(node.val);
//将该节点的左右子节点入队列
if (node.left != null) {
nodes.add(node.left);
}if (node.right != null) {
nodes.add(node.right);
}
}
allResults.add(results);
}
return allResults;
}
就相当于刚开始把公司老总放入队列,这是第一层,然后把老总的直接下级比如:vp,总监等,取出
来,然后放入队列,到了vp,总监这一层时,再把他们的直接下属放入队列。
在图中的广度优先搜索过程如下:
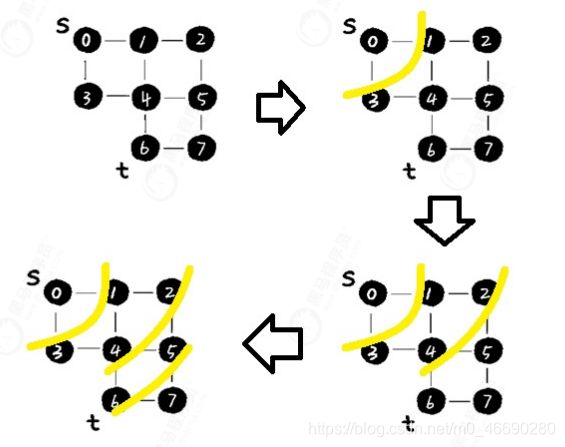
参考该网址上的演示过程:https://visualgo.net/zh/dfsbfs
应用特点:
1:BFS适合在树或图中求解最近,最短等相关问题
2:DFS适合在树或图中求解最远,最深等相关问题
3:实际应用中基于图的应用居多
面试实战
102. 二叉树的层序遍历
https://leetcode-cn.com/problems/binary-tree-level-order-traversal/
典型的BFS,借助队列FIFO特性
public List<List<Integer>> levelOrder(TreeNode root) {
if(root==null){
return new ArrayList();
}
List<List<Integer>>res=new ArrayList();
Queue<TreeNode>queue=new LinkedList();
queue.add(root);
while(!queue.isEmpty()){
int size=queue.size();
List<Integer>list=new ArrayList();
for(int i=0;i<size;i++){
TreeNode node=queue.poll();
list.add(node.val);
if(node.left!=null){
queue.add(node.left);
}
if(node.right!=null){
queue.add(node.right);
}
}
res.add(list);
}
return res;
}
时间复杂度O(n),空间复杂度O(n)
进阶:能否基于DFS完成
思路:按照深度优先遍历,遍历过程中将当前节点的值添加到它所对应的深度的集合中。因此需要一个在dfs
过程中代表深度的变量
public List<List<Integer>> levelOrder(TreeNode root) {
if(root==null){
return new ArrayList();
}
List<List<Integer>>res=new ArrayList();
dfs(root,0,res);
return res;
}
public void dfs(TreeNode root,int level,List<List<Integer>> res){
if(root==null){
return;
}
int size=res.size();
if(level>size-1){
res.add(new ArrayList());
}
List<Integer>list=res.get(level);
list.add(root.val);
dfs(root.left,level+1,res);
dfs(root.right,level+1,res);
}
104. 二叉树的最大深度
https://leetcode-cn.com/problems/maximum-depth-of-binary-tree/

如果我们知道了左子树和右子树的最大深度 l 和 r,那么该二叉树的最大深度即为
max(l,r)+1
而左子树和右子树的最大深度又可以以同样的方式进行计算。因此使用递归
其实这也是DFS的体现,直接下探到最深处得到最大深度,然后左右两边比较即可。
public int maxDepth(TreeNode root) {
if(root==null){
return 0;
}
return Math.max(maxDepth(root.left),maxDepth(root.right))+1;
}
时间复杂度:O(n),其中 n 为二叉树节点的个数。每个节点在递归中只被遍历一次。
空间复杂度:O(height),其中height 表示二叉树的高度。递归函数需要栈空间,而栈空间取决于递归的
深度,因此空间复杂度等价于二叉树的高度。
进阶:能否用BFS完成
利用一个计数器,每遍历完一层就计一个数,直到所有层都遍历结束
public int maxDepth(TreeNode root) {
if(root==null){
return 0;
}
Queue<TreeNode>queue=new LinkedList();
queue.add(root);
int deep=0;
while(!queue.isEmpty()){
int size=queue.size();
for(int i=0;i<size;i++){
TreeNode node= queue.poll();
if(node.left!=null){
queue.add(node.left);
}
if(node.right!=null){
queue.add(node.right);
}
}
deep++;
}
return deep;
}
小结:
在实际应用中,DFS要比BFS应用的广泛!
515. 在每个树行中找最大值
https://leetcode-cn.com/problems/find-largest-value-in-each-tree-row/

典型的BFS
public List<Integer> largestValues(TreeNode root) {
if(root==null){
return new ArrayList();
}
List<Integer>res=new ArrayList();
Queue<TreeNode>queue=new LinkedList();
queue.add(root);
while(!queue.isEmpty()){
int size=queue.size();
int max=Integer.MIN_VALUE;
for(int i=0;i<size;i++){
TreeNode node= queue.poll();
max=Math.max(max,node.val);
if(node.left!=null){
queue.add(node.left);
}
if(node.right!=null){
queue.add(node.right);
}
}
res.add(max);
}
return res;
}
200. 岛屿数量
https://leetcode-cn.com/problems/number-of-islands/

典型的图的搜索,立马想到DFS和BFS
//定义上下左右的方向盘,各走一步的信息
int [][]direction={{0,1},{0,-1},{1,0},{-1,0}};
//定义网络的行数
int rows;
//定义网络的列数
int colus;
public int numIslands(char[][] grid) {
rows=grid.length;
if(rows==0){
return 0;
}
colus=grid[0].length;
//记录岛屿的总数
int count=0;
//定义网络各定点是否被访问过
boolean[][]visted=new boolean[rows][colus];
//找岛屿
for(int i=0;i<rows;i++){
for(int j=0;j<colus;j++){
//如果是岛屿,并且没有被访问过,使用深度优先搜索定点相连的陆地
if(grid[i][j]=='1'&&!visted[i][j]){
dfs(i,j,visted,grid);
//找到一块+1
count++;
}
}
}
return count;
}
//搜索与x,x相连的陆地顶点,并标记这些顶点
public void dfs(int x,int y,boolean[][]visted,char[][] grid){
//走过的顶点要标记
visted[x][y]=true;
//从该顶点,向上下左右四个方向走
for(int i=0;i<4;i++){
// direction[i]分别代表上下左右四个方向 direction[i][0]是X轴坐标要走的距离
int newX=x+direction[i][0];
int newY=y+direction[i][1];
//如果新顶点在网格内,且是陆地,且没有访问过,则继续搜索下去
if(inGrid(newX,newY)&&grid[newX][newY]=='1'&&!visted[newX][newY]){
dfs(newX,newY,visted,grid);
}
}
}
//检查顶点(x,y)是否在网格内
public boolean inGrid(int x,int y){
return x>=0&&x<rows&&y>=0&&y<colus;
}
拓展
127. 单词接龙
https://leetcode-cn.com/problems/word-ladder/
126. 单词接龙2
https://leetcode-cn.com/problems/word-ladder-ii/
529. 扫雷游戏
https://leetcode-cn.com/problems/minesweeper/
36. 有效的数独
https://leetcode-cn.com/problems/valid-sudoku/
2、贪心算法
贪心算法(英语:greedy algorithm),又称贪婪算法,是一种在每一步选择中都采取在当前状态下最好或最优(即最有利)的选择,从而希望导致结果是最好或最优的算法。
贪心:当下做局部最优判断,不会回退
回溯:能够回退撤销选择
看这个算法的名字:贪心,贪婪,两个字的含义最关键,好像一个贪婪的人所有事情都只想到眼前,看不到长远,也不为最终的结果和将来着想,贪图眼前局部的利益最大化。
322. 零钱兑换
贪心算法可以解决一些最优化问题,比如:求图的最小生成树,求哈夫曼编码等等。然后对于工程和生活中的一些问题,贪心法一般不能得到我们想要的最终答案,因为每一步都找局部最优并不一定导致全局最优。
比如leetcode:322. 零钱兑换
https://leetcode-cn.com/problems/coin-change/submissions/

场景1:假设当前可选硬币集合为:coins=[20,10,5,1],求可以凑成总金amount=36 所需的最少的硬币个数?
这时就可以用贪心法,每次都先选最大的面额

基于贪心的思路我们可以写出第一版代码:
class Solution {
public int coinChange(int[] coins, int amount) {
if(amount==0){
return 0;
}
int count=0;
Arrays.sort(coins);
for(int i=coins.length-1;i>=0;i--){
int current=amount/coins[i];
if(current==0){
continue;
}
amount=amount-current*coins[i];
count+=current;
if(amount==0){
return count;
}
}
return -1;
}
}
提交测试,有些测试用例能通过,但有些不行,譬如:输入如下测试用例
[10,9,1] 18

但是如果用贪心算法来求解的话,应该是如下的情况:

进阶:当贪心算法失效了怎么办?如何优化?
思路:可以通过回溯来解决“过于贪心”的问题,简单的说就是加入一个递归搜索过程,穷举所有结果,通过记录所有解中最小的那个得到最优解,即使用硬币数最少。
1:每种硬币有[0,maxCount]个选择,其中maxCount= amount / coins[i],可以看作是选择列表
2:从选择列表中选择一个,然后递归到下一个硬币,搜索所有组合结果
3:整个过程中记录组合结果中使用硬币最少的解,即为题目要求的解。
直接使用DFS回溯的话肯定是能够得到准确答案的,但是效率会非常低;因此在这里使用贪心+回溯相配合的方式,先尽可能的使用大面值的coins,如果此路不通则慢慢减少大面值coins的数量直至为0;这里还是用的一个剪枝的技巧:尽早的判断这条路走下去会不会可能是最优解。这里就是时刻判断:如果使用这种coin,则使用coins的总数量是不是已经超过了之前的方案,如果超过的话说明这条路即便是通了也不可能是最优解。
class Solution {
public void sort(int[]coins){
先排序,搞成从大到小
Arrays.sort(coins);
int n = coins.length-1;
int temp;
for (int i=0;i<=(n-1)/2;i++) {
temp = coins[i];
coins[i] = coins[n-i];
coins[n-i] = temp; }
}
int minCount=Integer.MAX_VALUE;
public int coinChange(int[] coins, int amount) {
sort(coins);
dfs(coins,amount,0,0);
if(minCount==Integer.MAX_VALUE){
return -1;
}
return minCount;
}
public void dfs(int[]coins,int amount,int selecount,int startIndex){
//如果值为0,终止
if(amount==0){
if(selecount<minCount){
minCount=selecount;
}
}
if(startIndex>coins.length-1){
return;
}
//计算当前使用最多硬币的数量
int resultCount=amount/coins[startIndex];
//从列表中【0,maxcount】中选择,然后递归到下一个硬币
for(int i=resultCount;i>=0&&selecount+i<minCount;i--){
//每一次需要剩余的额度
int result=amount-coins[startIndex]*i;
//这里无需显示的撤销选择,for循环继续走选择下一个就相当于在回溯了,我们无需记走过的 路径和每种走法,我们只是在走的过程中记步数。
dfs(coins,result,selecount+i,startIndex+1);
}
}
}
贪心算法的局限性:
贪心算法总是以局部最优来解决问题,只考虑“当前”的最大利益,既不向前多看一步,也不向后多看一步,导致每次都只用当前阶段的最优解,那么如果纯粹采用这种策略我们就永远无法达到整体最优,有时候也就无法求得题目最终的答案了。
虽然纯粹的贪心算法作用有限,但是这种求解局部最优的思路在方向上肯定是对的,毕竟所谓的整体最优肯定是从很多个局部最优中选择出来的,因此所有最优化问题的基础都是贪心算法
贪心算法的适用场景:
一旦一个问题可以通过贪心算法来解决,那么贪心算法一般是解决这个问题的最好办法。因此一般遇到一个问题的时候重点是要能证明该问题能够用贪心算法来求解。
求最值等系列问题,而求最值的核心思想是穷举。这是因为只要我们能够找到所有可能的答案,从中挑选出最优的解就是算法问题的结果。在没有优化的情况下,穷举从来就不算是一个好方法。使用贪心算法来解题是一种使用局部最优思想解题的算法(即从问题的某一个初始解出发逐步逼近给定的目标,以尽可能快的速度去求得更好的解,当达到算法中的某一步不能再继续前进时,算法停止)。
我们往往需要使用回溯(搜索)来优化贪心算法,否则就会导致算法失效。因此,在求解最值问题时,我们需要更好的方法来解。在后面课程讲到递归和穷举优化问题的时候,会讲到解决最值问题的正确思路和方法:考虑整体最优的问题。
由于贪心法的高效性以及所求得的答案比较接近最优结果,贪心法也可以用作辅助算法或者直接解决一些要求结果不是特别精确的问题。
面试实战
455. 分发饼干
https://leetcode-cn.com/problems/assign-cookies/

public int findContentChildren(int[] g, int[] s) {
此处贪心的整体思路是:最小尺寸的饼干发给最小胃口的孩子,即保证:给每个孩子分配的饼干既能满足他 的胃口又还不浪费饼干,
//对胃口值和饼干尺寸排序,
Arrays.sort(g);
Arrays.sort(s);
//定义两个数组下标-也是双指针思想的体现
int i=0;
int j=0;
int count=0;
while(i<g.length&&j<s.length){
//j饼干能满足i孩子,然后看下一块饼干和下一个孩子
if(s[j]>=g[i]){
i++;j++;count++;
}else{
//j饼干不能满足i孩子,看下一块饼干是否能满足
j++;
}
}
return count;
}
进阶:想想如何去论证贪心算法在该场景中,每次使用局部最优解能保证最终的最优解呢?
可参考题解:https://leetcode-cn.com/problems/assign-cookies/solution/tan-xin-jie-fa-by-cyc2018/
的论述。
122. 买卖股票的最佳时机 II
https://leetcode-cn.com/problems/best-time-to-buy-and-sell-stock-ii/submissions/
股票买卖系列问题典型的解法是动态规划,但是针对这道题的特殊解法可以是用贪心。
可以参考精选题解
精选题解1的方法3
精选题解2

public int maxProfit(int[] prices) {
int maxProfit=0;
if(prices.length<2){
return maxProfit;
}
for(int i=0;i<prices.length;i++){
如果今天价格比前一天高,则在前一天买入,今天卖出
if(i>0&&prices[i]>prices[i-1]){
maxProfit+=prices[i]-prices[i-1];
}
}
return maxProfit;
}
55. 跳跃游戏
https://leetcode-cn.com/problems/jump-game/

public boolean canJump(int[] nums) {
int fast=0;//定义最远距离
for(int i=0;i<nums.length;i++){
//用来判断到某个为止后再走不下去【3,2,1,0,4】
if(i>fast){
return false;
}
fast=Math.max(fast,nums[i]+i);
if(fast>=nums.length-1){
return true;
}
}
return false;
}
45. 跳跃游戏 II
https://leetcode-cn.com/problems/jump-game-ii/

典型的贪心算法,通过局部最优解得到全局最优解
请参考官方题解:https://leetcode-cn.com/problems/jump-game-ii/solution/tiao-yue-you-xi-ii-byleetcode-solution/中的方法二
class Solution {
public int jump(int[] nums) {
//边界位置
int boundary=0;
//最远位置的点
int maxPoint=0;
//步数
int stepCount=0;
/* 在遍历数组时,我们不访问最后一个元素,这是因为在访问最后一个元素之前,我们的边界一定大于 等于最后一个位置, 否则就无法跳到最后一个位置了。 如果访问最后一个元素,在边界正好为最后一个位置的情况下,我们会增加一次「不必要的跳跃次 数」 */
for(int i=0;i<nums.length-1;i++){
//找最远位置的点
maxPoint=Math.max(maxPoint,nums[i]+i);
//i走到边界后,更新边界并增加跳跃次数
if(i==boundary){
boundary=maxPoint;
stepCount++;
}
}
return stepCount;
}
}
860. 柠檬水找零
https://leetcode-cn.com/problems/lemonade-change/

官方题解
class Solution {
public boolean lemonadeChange(int[] bills) {
//定义5元,10元钞票的张数
int five=0;
int ten=0;
for(int bill:bills){
if(bill==5){
//不需找零,
five++;
}else if(bill==10){
//需要找零5块,没有5块则找零失败
if(five>0){
five--;
ten++;
}else{
return false;
}
}else {
//需要找零15,按照贪心思想,先找面额大的组合,这样最有利 10+5
if(five>0&&ten>0){
ten--;
five--;
}else if(five>2){
// 如果没有10+5,找三个5块也行
five-=3;
}else{
//找零失败
return false;
}
}
}
return true;
}
}
3、二分查找
二分查找(Binary Search)算法,也叫折半查找算法。
3.1原理分析
二分查找是一种非常简单易懂的快速查找算法,其思想在生活中随处可见,比如朋友聚会的时候爱玩的一个猜数游戏,我随机写一个0-100之间的数字,然后大家依次来猜,猜的过程中大家每猜一次我都会告诉大家猜大了还是猜小了,直到有人猜中为止,猜中的人会有一些惩罚措施。这个过程其实就是二分查找思想的一种体现。
回到实际的开发场景中,假设有10个订单,其金额分别是:6,12,15,19,24,26,29,35,46,67。请从中找出订单金额为15的订单,利用二分查找的思想我们每次都与区间中间的数据进行大小的比较以缩小查找的范围,下面这幅图代表了查找的过程,其中 low,high代表了待查找区间的下标,mid表示待查找区间中间元素的下标(如果范围区间是偶数个导致中间数有两个就选择较小的那个)

通过这个查找过程我们可以对二分查找的思想做一个汇总:二分查找针对的是一个有序的数据集合,查找思想有点类似分治思想。每次都通过跟区间的中间元素对比,将待查找的区间缩小为之前的一半,直到找到要查找的元素,或者区间被缩小为 0
3.2、复杂度分析
理解了二分查找的思想后我们来分析二分查找的时间复杂度,首先我们要明确二分查找是一种非常高效的查找算法,通过分析其时间复杂度我们就可以发现,我们假设数据大小为n,每次查找完后数据的大小缩减为原来的一半,直到最后数据大小被缩减为1此时停止,如果我们用数据来描述其变化的规律那就是:
n,n/2,n/4,n/8,n/16,n/32,…,1;
可以看出来,这是一个等比数列,当数据大小变为1时:

其中k 的值就是总共缩小的次数。而每一次缩小操作只涉及两个数据的大小比较,所以,经过了 k 次区间缩小操作,通过计算k的值我们可以得出二分查找的时间复杂度就是 O(logn)
这是一种非常高效的时间复杂度,有时候甚至比O(1)复杂度更高效,为什么这么说呢?因为对于log n来说即使n非常的大对应的log n的值也会很小,之前在学习O(1)复杂度时我们讲过O(1)代表的是一种常量级复杂度并不是说代码只需要执行一次,有时候可能要执行100次,1000次这种常数级次数的复杂度都可以用O(1)表示,所以,常量级时间复杂度的算法有时候可能还没有 O(logn) 的算法执行效率高。
1.3、代码实现
二分查找的实现方式有基于循环的实现方式,也有基于递归的方式,现给出这两种方式编写的代码模板
1、基于循环的二分查找代码模板
// 返回的是元素在数组中的下标
public int binarySearch(int[] array, int target) {
int left = 0, right = array.length - 1, mid;
while (left <= right) {
// mid = (left + right)>> 1 这里left+right不用防止最大值越界
mid = left + ((right - left) >>1) ;
if (array[mid] == target) {
return mid;
} else if (array[mid] > target) {
right = mid - 1;
} else {
left = mid + 1;
}
}
return -1;
}
用mid不断去逼近我们的目标值,相对好的情况直接在某段中间找到了目标值,最坏的情况是不断去逼近,最后left==right找到目标值,当然如果真的找不到目标值也就是left>right的时候。
2、基于递归的二分查找代码模板
public int recurBinarySearch(int[] array, int target,int left,int right) {
//terminal
if (left > right) {
return -1; }
//process current 计算中间元素的下标
int mid = left + ((right - left)>>1);
if (array[mid] == target) {
return mid;
}else if (array[mid] > target) {
//drill down
return recurBinarySearch(array,target,left,mid-1);
}else {
return recurBinarySearch(array,target,mid+1,right);
}
}
进阶:二分查找的实现我们可以分为两大类情况
1,有序数列中不存在重复元素的简单实现;
2:有序数列中存在重复元素的变形实现,
针对第一种,上面已经给出了代码模板,针对第二种,在实际的应用场景中可能会出现如下几种情况:
2.1、从数据序列中查找第一个值等于给定值的元素,比如在{6,12,15,19,24,26,29,29,29,67}中找第一个
等于29的元素
2.2、从数据序列中查找最后一个值等于给定值的元素。还是刚刚的元素序列,找最后一个等于29的元素
2.3、从数据序列中查找第一个大于等于给定值的元素。
2.4、从数据序列中查找出最后一个值小于等于给定值的元素。
课后思考:针对这四种情况,代码应该如何实现呢?
1.4、应用场景说明
二分查找的时间复杂度是O(log n),其效率非常高,那是不是说所有情况下都可以使用二分查找呢?下面我们讨论一下二分查找的应用前提
1、待查找的数据序列必须有序
二分查找对这一要求比较苛刻,待查找的数据序列必须是有序的(单调递增或者单调递减),假如数据无序,那我们要先排序,然后二分查找,如果我们针对的是一组固定的静态数据,也就说该数据序列不会进行插入和删除操作,那我们完全可以先排序然后二分查找,这样子一次排序多次查找;但是如果数据序列本身不是固定的静态的,可能涉及数据序列的插入和删除操作,那我们每次查找前都需要进行排序然后才能查找,这样子成本非常的高。
2、数据的存储依赖数组
待查找的数据序列需要使用数组进存储,也就是说依赖顺序存储结构。那难道不能用其他的结构来存储待查找的数据序列吗?比如使用链表来存储,答案是不可以的,通过我们前面实现的二分查找的过程可知,二分查找,算法需要根据下标,left,right,mid来访问数据序列中的元素,数组按照下标访问元素的复杂度是O(1),而链表访问元素的时间复杂度是O(n),因此如果使用链表来存储数据二分查找的时间复杂度就会变得很高。
3、数据序列存在上下边界
数据序列有上下边界,才能找到中间点,这样才能二分下去。
3、数据量太小或太大都不适合用二分查找
数据量很小的情况下,没有必要使用二分查找,使用循环遍历就够了,因为只有在数据量比较大的情况下二分
查找才能体现出优势,不过在某些情况下即使数据量很小也建议大家使用二分查找,比如数据序列中的数据都是一些长度非常长的字符串,这些长度非常长的字符串比较起来也会非常的耗时,所以我们要尽可能的减少比较的次数,这样反倒有助于提高性能。
那为什么数据量太大的情况下也不建议使用二分查找呢?因为我们前面刚讲到二分查找底层需要依赖数组存储
待查找的数据序列,而数组的特点是需要连续的内存空间,比如现在有1G的订单数据,如果用数组来存储就需要1G的连续内存,即便有2G的剩余内存空间,如果这2G的内存空间不连续那也无法申请到1G大小的数组空间,所以我们说数据量太大也不适合用二分查找。
34. 在排序数组中查找元素的第一个和最后一个位置
34. 在排序数组中查找元素的第一个和最后一个位置
class Solution {
public int[] searchRange(int[] nums, int target) {
int len=nums.length;
int left=0;
int right=len-1;
int mid=0;
while(left<=right){
mid=(right+left)/2;
if(target==nums[mid]){
int i=mid;
int j=mid;
while(i>=0&&nums[i]==target)i--;
while(j<len&&nums[j]==target)j++;
//各自遇到了不等于自己的元素
return new int[]{i+1,j-1};
}else if(target>nums[mid]){
left=mid+1;
}else {
right=mid-1;
}
}
return new int[]{-1,-1};
}
}
上面这种如果遇到相同数量比较多,会退化成O(n)的复杂度
完全二分法
class Solution {
public int[] searchRange(int[] nums, int target) {
if(nums==null||nums.length==0)return new int[]{-1,-1};
int first=SearchFirst(nums,target);
if(first==-1)return new int[]{-1,-1};
int last=SearchLast(nums,target);
return new int[]{first,last};
}
public int SearchFirst(int[] nums, int target){
int len=nums.length;
int left=0;
int right=len-1;
int mid=0;
while(left<right){
//不能相等,因为如果相等的话,left=2,right=2,会死循环
mid=(left+right)/2;
if(nums[mid]==target){
//5 7 7 8 8 8 10
//这里有细节,如果取前面那个的话,同时拿到了的话,说明右侧区间没有需要的target
//比如找到第二个8,要往前找才合理,而且因为可能是最后一个值,只能等于
right=mid;
}else if(nums[mid]<target){
left=mid+1;
}else{
right=mid-1;
}
}
if(nums[left]==target){
return left;
}else{
return -1;
}
}
public int SearchLast(int[] nums, int target){
int len=nums.length;
int left=0;
int right=len-1;
int mid=0;
while(left<right){
//加一是为了向后偏移一位,取后面一位
//如果是 5 7 7 8 8 10,位置移动到4 5也就是8 10的位置时,(4+5)/2=4也就是一直往左偏,导致死循环
mid=(left+right+1)/2;
if(nums[mid]==target){
//5 7 7 8 8 10 如果拿到值了,要往后走
left=mid;
}else if(nums[mid]<target){
left=mid+1;
}else{
right=mid-1;
}
}
if(nums[left]==target){
return left;
}else{
return -1;
}
}
}
74. 搜索二维矩阵
74. 搜索二维矩阵
class Solution {
public boolean searchMatrix(int[][] matrix, int target) {
int i=matrix.length-1;
int j=0;
while(i>=0&&j<matrix[0].length){
if(matrix[i][j]>target){
i--;
}else if(matrix[i][j]<target){
j++;
}else{
return true;
}
}
return false;
}
}
2、面试实战
69. x 的平方根
https://leetcode-cn.com/problems/sqrtx/

class Solution {
public int mySqrt(int x) {
if(x<=1){
return x;
}
// 求sqrt(x)即求:x=n^2 (n>0),就是我们所熟知的抛物线(y=x^2)右侧,单调递增,且有上下界,[1,x/2]
long left=1;
long right=x>>1;
long mid=0;
//找一个数k,k^2<=x,找一个最大的k就是我们想要的
while(left<=right){
mid=(left+right)>>1;
if(mid*mid<x){
left=mid+1;
}else if(mid*mid>x){
right=mid-1;
}else {
return (int)mid;
}
}
return (int)left-1;
}
}
代码解释:
1:如果正好找到一个mid^2 = x则在while loop中就可以直接返回了,
2:如果while loop中还没找到,就类似x=8,我们在[ 1,2,3,4 ]中去寻找,while loop中最后一次循
环left == right == 3,我们只需找k^2 <=x的最大k值即可。
进阶:牛顿迭代法解决该问题!
参考精选题解:
https://leetcode-cn.com/problems/sqrtx/solution/erfen-cha-zhao-niu-dun-fa-python-dai-ma-by-liweiw/ 方法二
同类题目:367. 有效的完全平方数
https://leetcode-cn.com/problems/valid-perfect-square/submissions/
class Solution {
public boolean isPerfectSquare(int num) {
if(num<=1){
return true;
}
long left=1,right=num>>1,mid=0;
while(left<=right){
mid=(left+right)>>1;
if(mid*mid>num){
right=mid-1;
}else if(mid*mid<num){
left=mid+1;
}else{
return true;
}
}
return false;
}
}
33. 搜索旋转排序数组
https://leetcode-cn.com/problems/search-in-rotated-sorted-array/

二分查找的变形题目
思考要点:
1:二分的条件:满足有上下边界,数组存储可利用下标获取,单调性这块原始数组是单调递增的,旋转之后虽然整体不是单调性的,但是其中有一半一定是单调递增的。
2:要达到log n的复杂度肯定是要二分,但是并不能简单套用二分的模板,我们需要先找到哪半部分是具备单调性的,并判断target是否在该范围内,如果在则在这部分查找target,如果不在则在另外半部分查找。

class Solution {
public int search(int[] nums, int target) {
//此处left,right代表的是下标
int left=0;
int right=nums.length-1;
int mid=0;
while(left<=right){
mid=left+(right-left>>1);
if(nums[mid]==target){
return mid;
}
//前半部分有序
if(nums[left]<=nums[mid]){
//target如果在前半部分则在前半部分找,否则在后半部分找
if(target<nums[mid]&&target>=nums[left]){
right=mid-1;
}else{
left=mid+1;
}
}else{
//后半部分有序
//target如果在后半部分则在后半部分找,否则在前半部分找
if(target>nums[mid]&&target<=nums[right]){
left=mid+1;
}else{
right=mid-1;
}
}
}
return -1;
}
}
153. 寻找旋转排序数组中的最小值
https://leetcode-cn.com/problems/find-minimum-in-rotated-sorted-array/submissions/


class Solution {
public int findMin(int[] nums) {
int left=0;
int right=nums.length-1;
int mid=0;
/* 在这里如果left==right则可以直接返回了,最小元素一定是它 */
while(left<right){
mid=left+(right-left>>1);
if(nums[mid]<nums[right]){
//右区间连续,最小值一定在左半区间
//mid可能是最小值也可能不是,简单二分的模板代码写right=mid-1;
right=mid;
}else{
//右边区间不连续,最小值一定在该区间内
left=mid+1;
}
}
return nums[left];
}
}
74. 搜索二维矩阵
https://leetcode-cn.com/problems/search-a-2d-matrix/submissions/

class Solution {
public boolean searchMatrix(int[][] matrix, int target) {
//标准的二分m x n的矩阵可以看成 m x n 的有序数组
int n=matrix.length;
if(n==0){
return false;
}
int m=matrix[0].length;
int left=0,right=n*m-1;
int mid=0, row=0, colus=0;
while(left<=right){
mid=left+(right-left>>1);
//mid=(left+right)>>1;
//最重要的就是将mid转换陈二维数组中的下标
row=mid/m;
colus=mid%m;
if(matrix[row][colus]==target){
return true;
}else if(matrix[row][colus]<target){
left=mid+1;
}else{
right=mid-1;
}
}
return false;
}
}
