算法设计-hw2
一、从分治到动态规划
1.1 动态规划的性质
动态规划具有以下三个明显特性:
- 无后效性:如果给定某一阶段的状态,则在这一阶段以后过程的发展不受这阶段以前各段状态的影响。如果说的直白一些,就是当我们求出 d p i dp_i dpi 的时候,我们是怎样求出来的,就不用管了,我们只需要利用 d p i dp_i dpi 就可以了。类似于“只要上了北航,没人管你到底是从河北考上的的,还是从月球考上的,大家只认为你是一个北航学生。”
- 最优子结构:规模大的最优化问题包含规模小的最优化问题,大问题的最优解可以由小问题的最优解推出。
- 重叠子问题:子问题的解不止会被利用一次。
虽然这三个特性都被称为“动态规划”的特性,但是“无后效性”和“最优子结构”并非是动态规划的专利。对于“无后效性”,应该是所有的分治算法都具有这个特性,如果我们必须掌握子问题的求解过程,那么显然我们就没必要将大问题分治为小问题。对于“最优子结构”,虽然“最优”二字将问题划定成了“最优化算法”的范畴,但是如果扩充最优化的定义,会发现依然几乎所有分治算法都满足具有最优子结构的定义。
所以从本质上来说,只有重叠子问题是动态规划的独有特性。并不是所有的分治算法都具有重叠子问题,比如说对于二叉树的遍历可以看做一个分治算法,但是对于每个子树的遍历,都没法用于其他的子树的遍历(勉强意思一下)。在《算法导论》中,有些问题是“树形”的,有些问题是“图形”的,动态规划适用的范围就是那种图形的最优化问题。
1.2 问题的难点
自底向上的动态规划的难点大概有两个:
- 确定具有无后效性的最优子结构。
- 分析重叠子问题的计算路径。
在 1.1 中已经阐述过了,第一个难点本质不是动态规划的难点,即使用分治算法,依然具有这个难点。而这个难点无疑是最难的,比如说我到现在依然不清楚,在背包问题中,明明是“平权”的物体,却要考虑“一个”和“前面多个”的关系,而不是“一个”和“其他的所有”的关系。现在看上去,“前面多个”就是一种最优子结构,而这却在我这里却并不自然。
关于如何确立最优子结构,只能说这是天才的领域,多亏了香子,才让我在对于这个问题的思考上更近了一步,但是依然没有办法将其转换成一个很容易的问题。
关于重叠子问题的计算路径,我们需要确定一个路径,去保证当一个最优化问题求解的时候,他求解依赖的最优化子问题已经被求解了。如果是“带备忘录的递归动态规划”,这个问题是不用考虑的,因为递归是自顶向下的过程中,是先“确立需求”,然后“实现需求”的过程,所以根本不需要在意计算顺序,它的计算路径是在递归的过程中自然确立的。但是对于纯正的“自底向下的迭代动态规划”,需要自行确定计算路径。这个部分我之前没有意识到,现在意识到了不同的子问题分割方式,会导致不同的计算路径,所以特意总结了一章。
这个部分是比较机械化的,大概只有几种类型。不过有意思的是,其实只要限制住了这个部分,其实最优子结构的形式也受到了一定的固化。所以只能有两个可能的推论:
- 确定最优子结构是可以更加机械化的。
- 机械化的计算路径就是一个笑话。
1.3 香子无后效性
虽然香子不承认,但是我确实是在与香子的交谈中获得了这部分的启发。以小跳蛙为例,在题目中出现的变量有“跳跃步数”和“所在石块”,这个问题的最优结构是 d p [ 所在块数 ] dp[所在块数] dp[所在块数] ,与跳跃步数无关。我们做状态转移的时候,考虑的是所在块数这个变量,而不考虑跳跃步数。所以感觉这两个变量必然存在一定的区别。区别他们就是确定“最优子问题结构”的一个步骤。
如果一个变量会对状态转移造成影响(效用),那么它就不具有“香子无后效性”。对于没有“香子无后效性”的变量,那么就应当将其作为状态变量。(这一章都是显然的废话)。
二、计算路径
2.1 行列遍历
这是最为普通的方法,出现在 0-1 背包问题, 编辑距离等景点问题中,对于这种情况,其状态转移方程往往呈现
d p j → d p i ( j ≤ i ) d p x , y → d p i , j ( x ≤ i , y ≤ j ) dp_j \rightarrow dp_i \quad (j \leq i) \\ dp_{x, y} \rightarrow dp_{i, j} \quad (x \leq i, y \leq j) dpj→dpi(j≤i)dpx,y→dpi,j(x≤i,y≤j)
的特征,如果是二维状态,那么就是当前单元格只依赖与其左上角区域的单元格,如图所示:
那么其计算路径就是:
2.2 斜向遍历
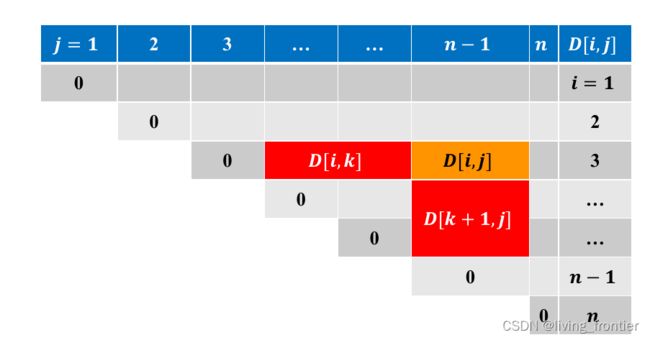
经典例题就是矩阵链乘法,在题目中出现的括号匹配问题。其状态转移方程呈现
( d p l e f t , m i d d l e , d p m i d d l e + 1 , r i g h t ) → d p l e f t , r i g h t ( l e f t ≤ m i d d l e < r i g h t ) (dp_{left, middle}, dp_{middle + 1, right}) \rightarrow dp_{left, right} \quad (left \leq middle < right) (dpleft,middle,dpmiddle+1,right)→dpleft,right(left≤middle<right)
其填表的结构更加典型,只有上三角,而且基准情况出现在对角线。
其顺序是斜向填写,即
而在实际实现的时候,需要先对与长度进行遍历(比较显然,就是只有先确定了长度比较小的子问题,然后才可以确定长度比较大的子问题),也就是长度即规模的思想。
代码如下(括号匹配)
#include 2.3 排序遍历
这个是一个很有意思的东西,例题是箱子问题
在获得箱子数组后,需要对于这个数组进行一个排序,让标号小的箱子不可能堆叠在标号大的箱子上(即标号大的箱子可能可以堆叠在标号小的箱子上)。我本来以为这是一个神来之笔。但是实际上这是确立计算路径的一种方式。
如果从自顶向下的角度来看,这个排序是没有必要的,用递归来解的话,大概是这样的
// 备忘录
int memo[3 * N];
int topHeight(int topCur)
{
if (memo[topCur])
{
return memo[topCur];
}
else
{
// 直接放在地上
int maxHeight = boxes[topCur].height;
// 放在某个箱子上
for (int i = 0; i < n; i++)
{
// 如果可以放置
if (boxes[topCur].isSmaller(boxes[i]))
{
maxHeight = max(maxHeight, boxes[topCur].height + topHeight(i));
}
}
cout << boxes[topCur] << " top height : " << maxHeight << endl;
// 记忆化
memo[topCur] = maxHeight;
return maxHeight;
}
}
但是在自底向下的时候,排序就变成必要的了,因为在不排序的时候,依赖是可能出现在当前状态之后的(即标号比当前状态大)
但是排序后,依赖状态一定先于当前状态求解,这十分美妙。
最后给出这道题两种解法的实现代码:
#include三、CPP 语法
3.1 string
可以直接用字符串字面量赋值
string s = "([(])]))"
可以获得长度,是不考虑结尾的 '/0' 的。
s.length();
可以用中括号访问元素(与字符数组一模一样)
(s[left] == '(' && s[right] == ')') || (s[left] == '[' && s[right] == ']')
可以使用 cin
cin >> s;
3.2 结构体初始化
结构体似乎默认全是 public
struct Box
{
int length;
int width;
int height;
Box()
{
this->length = 0;
this->width = 0;
this->height = 0;
}
Box(int length, int width, int height)
{
this->length = max(length, width);
this->width = min(length, width);
this->height = height;
}
};
如果想要初始化一个结构体
Box boxes[3 * N];
boxes[boxCur++] = Box(length, width, height);
两种方式都可以,另外字面量也可以,即
Box box = {1, 2, 3};
或者先声明,后修改
Box box;
box.height = 1;
box.width = 2;
box.length = 3;
3.3 结构体排序
利用 sort 函数可以完成排序,有两种形式
sort(begin_iter, end_iter);
sort(begin_iter, end_iter, comparator);
对于第一个,会调用默认的 < 进行比较,如果需要重新定义比较方式,那么就需要重载 < 符号。如下所示:
Box boxes[3 * N];
struct Box
{
int length;
int width;
int height;
bool operator <(const Box& other) const
{
return length >= other.length;
}
};
sort(boxes, boxes + n);
对于第二个,需要写一个比较函数
bool cmp(Box a, Box b)
{
return a.length >= b.length;
}
sort(boxes, boxes + n, cmp);
3.4 结构体输出
这个就标准写法了,之所以是友元函数,主要是方便访问内部属性。
friend ostream& operator<<(ostream& os, const Box& box)
{
os << "[" << box.length << ", " << box.width << ", " << box.height << "]";
return os;
}
3.5 stack
挺容易的,pop(), top(), push(), empty(), size() 都和 Java 比较类似。此题用栈实现了一个逆序输出
// 利用栈输出
stack<Box> ans;
do
{
ans.push(boxes[maxCur]);
maxCur = rec[maxCur];
}while(rec[maxCur]);
int cur = 1;
while (!ans.empty())
{
cout << cur++ << " floor : " << ans.top() << endl;
ans.pop();
}