Pytorch 自定义激活函数前向与反向传播 Tanh
看完这篇,你基本上可以自定义前向与反向传播,可以自己定义自己的算子
文章目录
-
- Tanh
-
- 公式
- 求导过程
- 优点:
- 缺点:
- 自定义Tanh
- 与Torch定义的比较
- 可视化
import matplotlib
import matplotlib.pyplot as plt
import numpy as np
import torch
import torch.nn as nn
import torch.nn.functional as F
%matplotlib inline
plt.rcParams['figure.figsize'] = (7, 3.5)
plt.rcParams['figure.dpi'] = 150
plt.rcParams['axes.unicode_minus'] = False #解决坐标轴负数的铅显示问题
Tanh
公式
tanh ( x ) = sinh ( x ) cosh ( x ) = e x − e − x e x + e − x \tanh(x) = \frac{\sinh(x)}{\cosh(x)} = \frac{e^x - e^{-x}}{e^x + e^{-x}} tanh(x)=cosh(x)sinh(x)=ex+e−xex−e−x
tanh ( x ) = 2 σ ( 2 x ) − 1 \tanh(x) = 2 \sigma(2x) - 1 tanh(x)=2σ(2x)−1
求导过程
tanh ′ ( x ) = ( e x − e − x e x + e − x ) ′ = [ ( e x − e − x ) ( e x + e − x ) − 1 ] ′ = ( e x + e − x ) ( e x + e − x ) − 1 + ( e x − e − x ) ( − 1 ) ( e x + e − x ) − 2 ( e x − e − x ) = 1 − ( e x − e − x ) 2 ( e x + e − x ) − 2 = 1 − ( e x − e − x ) 2 ( e x + e − x ) 2 = 1 − tanh 2 ( x ) \begin{aligned} \tanh'(x) =& \big(\frac{e^x - e^{-x}}{e^x + e^{-x}}\big)' \\ =& \big[(e^x - e^{-x})(e^x + e^{-x})^{-1}\big]' \\ =& (e^x + e^{-x})(e^x + e^{-x})^{-1} + (e^x - e^{-x})(-1)(e^x + e^{-x})^{-2} (e^x - e^{-x}) \\ =& 1-(e^x - e^{-x})^2(e^x + e^{-x})^{-2} \\ =& 1 - \frac{(e^x - e^{-x})^2}{(e^x + e^{-x})^2} \\ =& 1- \tanh^2(x) \\ \end{aligned} tanh′(x)======(ex+e−xex−e−x)′[(ex−e−x)(ex+e−x)−1]′(ex+e−x)(ex+e−x)−1+(ex−e−x)(−1)(ex+e−x)−2(ex−e−x)1−(ex−e−x)2(ex+e−x)−21−(ex+e−x)2(ex−e−x)21−tanh2(x)
优点:
Tanh也称为双切正切函数,取值范围为[-1,1]。tanh在特征相差明显时的效果会很好,在循环过程中会不断扩大特征效果。与 sigmoid 的区别是,tanh 是 0 均值的,因此实际应用中 tanh 会比 sigmoid 更好。文献 [LeCun, Y., et al., Backpropagation applied to handwritten zip code recognition. Neural computation, 1989. 1(4): p. 541-551.] 中提到tanh 网络的收敛速度要比sigmoid快,因为tanh 的输出均值比 sigmoid 更接近 0,SGD会更接近 natural gradient[4](一种二次优化技术),从而降低所需的迭代次数。非常优秀,几乎适合所有的场景
缺点:
- 该导数在正负饱和区的梯度都会接近于0值,会造成梯度消失。还有其更复杂的幂运算。
自定义Tanh
class SelfDefinedTanh(torch.autograd.Function):
@staticmethod
def forward(ctx, inp):
exp_x = torch.exp(inp)
exp_x_ = torch.exp(-inp)
result = torch.divide((exp_x - exp_x_), (exp_x + exp_x_))
ctx.save_for_backward(result)
return result
@staticmethod
def backward(ctx, grad_output):
# ctx.saved_tensors is tuple (tensors, grad_fn)
result, = ctx.saved_tensors
return grad_output * (1 - result.pow(2))
class Tanh(nn.Module):
def __init__(self):
super().__init__()
def forward(self, x):
out = SelfDefinedTanh.apply(x)
return out
def tanh_sigmoid(x):
"""according to the equation"""
# 2 * torch.sigmoid(2 * x) -1
return torch.mul(torch.sigmoid(torch.mul(x, 2)), 2) - 1
与Torch定义的比较
# self defined
torch.manual_seed(0)
tanh = Tanh() # SelfDefinedTanh
inp = torch.randn(5, requires_grad=True)
out = tanh((inp + 1).pow(2))
print(f'Out is\n{out}')
out.backward(torch.ones_like(inp), retain_graph=True)
print(f"\nFirst call\n{inp.grad}")
out.backward(torch.ones_like(inp), retain_graph=True)
print(f"\nSecond call\n{inp.grad}")
inp.grad.zero_()
out.backward(torch.ones_like(inp), retain_graph=True)
print(f"\nCall after zeroing gradients\n{inp.grad}")
Out is
tensor([1.0000, 0.4615, 0.8831, 0.9855, 0.0071],
grad_fn=)
First call
tensor([ 5.0889e-05, 1.1121e+00, -5.1911e-01, 9.0267e-02, -1.6904e-01])
Second call
tensor([ 1.0178e-04, 2.2243e+00, -1.0382e+00, 1.8053e-01, -3.3807e-01])
Call after zeroing gradients
tensor([ 5.0889e-05, 1.1121e+00, -5.1911e-01, 9.0267e-02, -1.6904e-01])
# self defined tanh_sigmoid
torch.manual_seed(0)
inp = torch.randn(5, requires_grad=True)
out = tanh_sigmoid((inp + 1).pow(2))
print(f'Out is\n{out}')
out.backward(torch.ones_like(inp), retain_graph=True)
print(f"\nFirst call\n{inp.grad}")
out.backward(torch.ones_like(inp), retain_graph=True)
print(f"\nSecond call\n{inp.grad}")
inp.grad.zero_()
out.backward(torch.ones_like(inp), retain_graph=True)
print(f"\nCall after zeroing gradients\n{inp.grad}")
Out is
tensor([1.0000, 0.4615, 0.8831, 0.9855, 0.0071], grad_fn=)
First call
tensor([ 5.0889e-05, 1.1121e+00, -5.1911e-01, 9.0267e-02, -1.6904e-01])
Second call
tensor([ 1.0178e-04, 2.2243e+00, -1.0382e+00, 1.8053e-01, -3.3807e-01])
Call after zeroing gradients
tensor([ 5.0889e-05, 1.1121e+00, -5.1911e-01, 9.0267e-02, -1.6904e-01])
# torch defined
torch.manual_seed(0)
inp = torch.randn(5, requires_grad=True)
out = torch.tanh((inp + 1).pow(2))
print(f'Out is\n{out}')
out.backward(torch.ones_like(inp), retain_graph=True)
print(f"\nFirst call\n{inp.grad}")
out.backward(torch.ones_like(inp), retain_graph=True)
print(f"\nSecond call\n{inp.grad}")
inp.grad.zero_()
out.backward(torch.ones_like(inp), retain_graph=True)
print(f"\nCall after zeroing gradients\n{inp.grad}")
Out is
tensor([1.0000, 0.4615, 0.8831, 0.9855, 0.0071], grad_fn=)
First call
tensor([ 5.0283e-05, 1.1121e+00, -5.1911e-01, 9.0267e-02, -1.6904e-01])
Second call
tensor([ 1.0057e-04, 2.2243e+00, -1.0382e+00, 1.8053e-01, -3.3807e-01])
Call after zeroing gradients
tensor([ 5.0283e-05, 1.1121e+00, -5.1911e-01, 9.0267e-02, -1.6904e-01])
从上3个结果,可以看出,不管是经过sigmoid来计算,还是公式定义都可以得到一样的output与gradient。但在输入的值较大时,torch应该是减去一个小值,使得梯度更小。
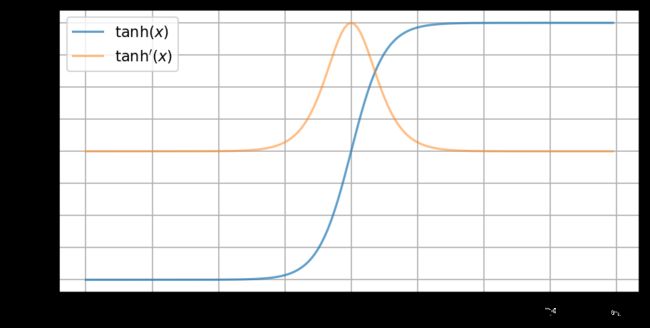
可视化
# visualization
inp = torch.arange(-8, 8, 0.1, requires_grad=True)
out = tanh(inp)
out.sum().backward()
inp_grad = inp.grad
plt.plot(inp.detach().numpy(),
out.detach().numpy(),
label=r"$\tanh(x)$",
alpha=0.7)
plt.plot(inp.detach().numpy(),
inp_grad.numpy(),
label=r"$\tanh'(x)$",
alpha=0.5)
plt.grid()
plt.legend()
plt.show()