【深度学习经典网络架构—1】：LeNet（附Keras实现）

✨博客主页：米开朗琪罗~
✨博主爱好：羽毛球
✨年轻人要：Living for the moment（活在当下）！
推荐专栏：【图像处理】【千锤百炼Python】【深度学习】【排序算法】

一、网络简介

LeNet是一个用于手写体字符识别非常高效的网络！

作者Yan LeCun于1998年提出该网络，也是后续各大神经网络的伊始！

论文链接：Gradient-based learning applied to document recognition

二、网络结构

图像经过LeNet的处理过程如下：

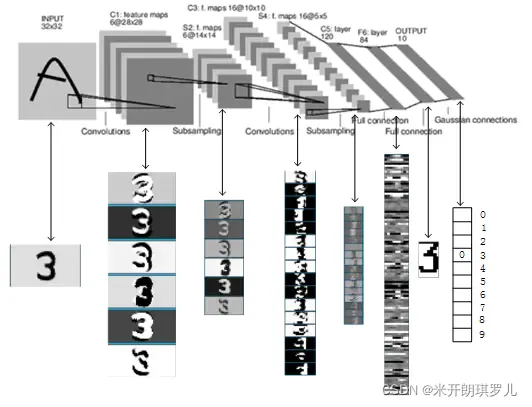
LeNet共有7层（不包括输入层）：卷积层—池化层—卷积层—池化层—卷积层—全连接层—全连接层

别看LeNet仅有7层，麻雀虽小，五脏俱全，包含有深度学习的基本模块（卷积层、池化层、全连接层）。

在介绍网络的每一个层之前，需要先了解卷积层输出特征图尺寸的计算，这里直接给出公式：
$$N=\frac{W-F+2P}{S}+1$$
其中各参数含义为：

参数	含义
N	输出特征图尺寸
W	输入特征图尺寸
F	卷积核尺寸
P	填充值大小
S	卷积核移动步长

这里的填充值P需要注意：

填充方式	P值
valid	0
same	与卷积核尺寸有关(F=1:P=0；F=3:P=1；F=5;P=3…)

LeNet网络的填充方式均为“valid”！

关于卷积网络的输入输出特征图关系具体可以参考这篇文章：

卷积网络（conv）中步长、填充、卷积核大小与输入输出大小的关系

2.1 INPUT层（输入层）

输入图像的尺寸统一归一化至32×32。

注：输入层一般不作为神经网络层结构之一。

2.2 C1层（卷积层）

类别	参数
输入特征图尺寸（输入图片）	32×32
卷积核尺寸	5×5
卷积核个数	6

2.2.1 输出特征图尺寸

$$N=\frac{32-5+2\times 0}{1}+1=28$$

2.2.2 训练参数

由于参数权值共享的原因，同一个卷积核的每一个神经元均使用相同的参数。
$$参数数量=(5\times 5+1)\times 6=156$$
这里5×5为卷积核尺寸，也即unit参数，1表示bias，6表示卷积核数量。

2.2.3 连接数

$$连接数=(5\times 5+1)\times 6\times (28\times 28)=122304$$
卷积后的图像尺寸为28×28，因此每个输出特征图有28×28个神经元。

2.3 S2层（池化层、下采样层）

类别	参数
输入特征图尺寸	28×28
池化尺寸	2×2
池化步长	2

2.3.1 输出特征图尺寸

$$N=\frac{28}{2}=14$$
通过池化区域为2、步长为2的最大池化层，可以对输入特征图实现降维，降维后的特征图尺寸是输入特征图尺寸的1/4。

2.3.2 训练参数

$$参数数量=2\times 6=12$$
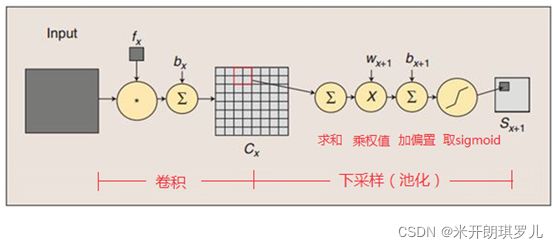
池化层是将C1卷积层中的2×2区域内的像素求和乘以一个权重再加上一个偏置，然后对该结果再做一次映射，因此每个池化核具有两个参数，所以一共包括2×6=12个训练参数。

卷积操作与池化操作的示意图如下：

引用：https://blog.csdn.net/daydayup_668819/article/details/79932548

2.3.3 连接数

$$连接数=(2\times 2+1)\times 6\times (14\times 14)=5880$$
卷积后的图像尺寸为14×14，因此每个输出特征图有14×14个神经元。

2.4 C3层（卷积层）

类别	参数
输入特征图尺寸	14×14
卷积核尺寸	5×5
卷积核个数	16

2.4.1 输出特征图尺寸

$$N=\frac{14-5+2\times 0}{1}+1=10$$

2.4.2 训练参数

引用： https://blog.csdn.net/daydayup_668819/article/details/79932548

需要注意的是，C3与S2并不是全连接而是部分连接，有些是C3连接到S2三层、有些四层、甚至达到6层，通过这种方式提取更多特征，连接的规则如下表所示：

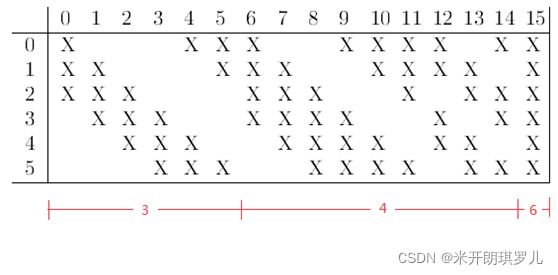
例如第一列表示C3层的第0个特征图（feature map）只跟S2层的第0、1和2这三个feature maps相连接，计算过程为：用3个卷积模板分别与S2层的3个feature maps进行卷积，然后将卷积的结果相加求和，再加上一个偏置，再取sigmoid得出卷积后对应的feature map了。其它列也是类似（有些是3个卷积模板，有些是4个，有些是6个）。因此，C3层的参数数目为：
$$参数数量=(5\times 5\times 3+1)\times 6+(5\times 5\times 4+1)\times 9+(5\times 5\times 6+1)\times 1=1516$$

2.4.3 连接数

$$连接数=1516\times (10\times 10)=1516004$$
卷积后的图像尺寸为28×28，因此每个输出特征图有28×28个神经元。

2.5 S4层（池化层、下采样层）

类别	参数
输入特征图尺寸	10×10
池化尺寸	2×2
池化步长	2

2.5.1 输出特征图尺寸

$$N=\frac{10}{2}=5$$
通过池化区域为2、步长为2的最大池化层，可以对输入特征图实现降维，降维后的特征图尺寸是输入特征图尺寸的1/4。

2.5.2 训练参数

$$参数数量=2\times 16=32$$
同S2计算方法相同。

卷积操作与池化操作的示意图如下：

2.5.3 连接数

$$连接数=(2\times 2+1)\times 16\times (5\times 5)=2000$$
卷积后的图像尺寸为5×5，因此每个输出特征图有5×5个神经元。

2.6 C5层（卷积层）

类别	参数
输入特征图尺寸	5×5
卷积核尺寸	5×5
卷积核个数	120

2.6.1 输出特征图尺寸

$$N=\frac{5-5+2\times 0}{1}+1=1$$
这里由于输入特征图尺寸为5×5，卷积核尺寸也为5×5，因此经过计算后，输出特征图尺寸为1×1，刚好构成了全连接！

2.6.2 训练参数

$$参数数量=120\times (5\times 5\times 16+1)=48120$$

2.6.3 连接数

$$连接数=48120\times 1\times 1=48120$$

2.7 F6层（全连接层）

类别	参数
输入维度	120
本层unit数	84

2.7.1 输出特征图尺寸

引用：https://blog.csdn.net/daydayup_668819/article/details/79932548

F6层有84个单元，之所以选这个数字的原因是来自于输出层的设计，对应于一个7×12的比特图，如下图所示，-1表示白色，1表示黑色，这样每个符号的比特图的黑白色就对应于一个编码。

该层有84个特征图，特征图大小与C5一样都是1×1，与C5层全连接。

2.7.2 训练参数

该层是全连接层，因此训练参数为：
$$参数数量=84\times (120+1)=10164$$

2.7.3 连接数

全连接层的连接数与训练参数一样：
$$连接数=84\times (120+1)=10164$$

2.8 OUTPUT层（全连接层、输出层）

类别	参数
输入维度	84
本层unit数	10

2.8.1 输出特征图尺寸

该层有10个特征图，特征图大小与C5、F6一样都是1×1，与F6层全连接。

2.8.2 训练参数

该层是全连接层，因此训练参数为：
$$参数数量=84\times 10=840$$

2.8.3 连接数

全连接层的连接数与训练参数一样：
$$连接数=84\times 10=840$$

注：输出层有10个节点，分别表示数字0-9，但输出的是位置信息，即如果第i个节点的值为0，则表示网络识别的结果是数字i。

三、Keras实现

3.1 程序编写

from keras.models import Sequential
from keras.layers import Dense, Flatten, Conv2D, MaxPool2D
import matplotlib.pyplot as plt
from keras.utils.vis_utils import plot_model

model = Sequential()

model.add(Conv2D(filters=6, kernel_size=(5, 5), padding='valid', input_shape=(32, 32, 1), activation='tanh'))
model.add(MaxPool2D(pool_size=(2, 2)))

model.add(Conv2D(filters=16, kernel_size=(5, 5), padding='valid', activation='tanh'))
model.add(MaxPool2D(pool_size=(2, 2)))

model.add(Flatten())

model.add(Dense(120, activation='tanh'))
model.add(Dense(84, activation='tanh'))
model.add(Dense(10, activation='softmax'))

print(model.summary())

plot_model(model, to_file='LeNet.png', show_shapes=True, show_layer_names=True, rankdir='TB')
plt.figure(figsize=(10, 10))
img = plt.imread('LeNet.png')
plt.imshow(img)
plt.axis('off')
plt.show()

3.2 打印模型信息

Model: "sequential"
_________________________________________________________________
Layer (type)                 Output Shape              Param #   
=================================================================
conv2d (Conv2D)              (None, 28, 28, 6)         156       
_________________________________________________________________
max_pooling2d (MaxPooling2D) (None, 14, 14, 6)         0         
_________________________________________________________________
conv2d_1 (Conv2D)            (None, 10, 10, 16)        2416      
_________________________________________________________________
max_pooling2d_1 (MaxPooling2 (None, 5, 5, 16)          0         
_________________________________________________________________
flatten (Flatten)            (None, 400)               0         
_________________________________________________________________
dense (Dense)                (None, 120)               48120     
_________________________________________________________________
dense_1 (Dense)              (None, 84)                10164     
_________________________________________________________________
dense_2 (Dense)              (None, 10)                850       
=================================================================
Total params: 61,706
Trainable params: 61,706
Non-trainable params: 0
_________________________________________________________________

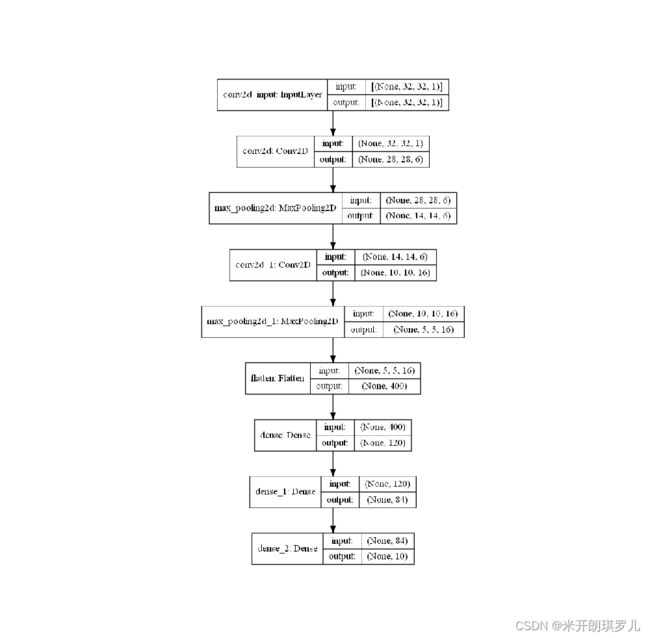
3.3 网络结构图可视化

四、总结

作为卷积神经网络的开山作，虽然现在LeNet已经逐步退出了深度学习舞台，但其影响力仍然存在，这也是计算机视觉经典网络的第一篇。