【数据结构】图文详解红黑树（从2-3查找树引入&&附C++代码）
文章目录
- 完美平衡
- 2-3查找树
-
- 基本概念
- 添加节点图解
- 红黑树
-
- 基本定义
- 红黑树的平衡化
-
- 左旋
- 右旋
- 红黑树的插入
-
- 向2节点插入
- 向3节点插入
- 红黑树的删除
完美平衡
我们知道二叉查找树其实就是基于二分的思想生成的，这时在这棵树上进行查找或者删除的时间复杂度为O(log(n))。但是某些时候，我们插入的数据顺序越是有序，这颗二叉树就越是不平衡（某个结点的左右子树高度差越大），此时生成的为搜索二叉树就退化成了一个链表，查找和删除的时间复杂度就趋近于O(n)。
故而我们在前一篇博客中提到了AVL树，可以借助旋转操作，维持二叉树的平衡，使得树中的每一个结点的平衡因子的绝对值都小于等于1。
但是我们认为这种平衡不是真正的平衡，真正的平衡是指树中的任意一个结点的左右子树高度都相等，所以就出现了一种完美平衡的概念如下：
完美平衡（Perfect balance）：每条从根节点到叶节点的路径的高度都是一样的（Every path from root to leaf has same length）。也就是每个节点的平衡因子为0.
为了得到这种完美平衡，我们引入2-3查找树。
2-3查找树
基本概念
2-3查找树在本指上不是一棵二叉树，而是一棵多叉树，同时还是一棵查找树，根结点大于所有左子孩子，小于所有右孩子。如果中序遍历2-3查找树，就可以得到排好序的序列。在一个完全平衡的2-3查找树中，根节点到每一个为空节点的距离都相同。
2-3树每个节点保存1个或者2个的key。对于普通的2节点(2-node)，要有1个key和左右两个子节点。对应3节点(3-node)，要有两个Key和三个子节点。
| 节点名 | key值个数 | 子节点树 |
|---|---|---|
| 2节点 | 1 | 2（二叉） |
| 3节点 | 2 | 3（三叉） |
对于普通的2节点我们可以直接使用二叉查找树理解节点大小关系，对于三节点则关系如下图：
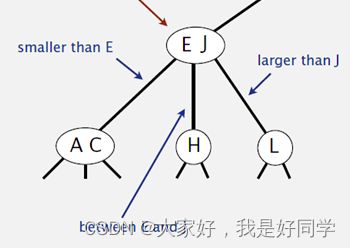
三节点中值大小关系：
- 有两个key值，如图中分别为E和J；
- 该结点的第一个key值一定大于它左孩子中的值，如图中E大于A和C；
- 该结点第二个key值一定小于它右孩子的所有值，如图中J大于L；
- 中间节点的值一定大于第一个key值，小于第二个key值，如图中，H大于E，且H小于J；
添加节点图解
- 插入值为1的新节点，如图：
- 插入值为2的新节点，若直接插入，此时值为1的节点的平衡因子为-1，就不是完美平衡了，所以我们要将其与第一个节点进行融合，形成一个三节点，如图：
3. 插入值为3的新节点，若直接插入，此时我们第二步得到的三节点的平衡因子为-1，故而我们将其与第三节点融合，但这样将会得到一个四节点，这样的节点不能在2-3查找树中存在，故而需要分解，得到如下的查找树：
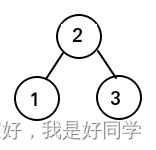
4. 插入一个值为4的节点，若直接插入以上得到的二叉树，此时这个新节点将会成为值为3的右节点，那么此是值位3的节点的平衡因子将不为0，故而，我们选择将这个新节点与3进行融合，成为一个三节点，如下图：
5. 插入一个值为5的新节点，若直接插入，则此时该新节点将会成为由3和4组成的三节点的右孩子，这显然将不会完美平衡，故而选择将其与三节点进行融合成一个四节点，然后将其进行分解，如图左；
这样显然还不是一个完美平衡的查找树，此时递归查看的时候判断得到的第一个不平衡的节点为值为4的节点，我们将这个节点和它的根结点进行融合，形成一个值为2，4的三节点，如图右，这时就得到了一个完美平衡的二叉树。
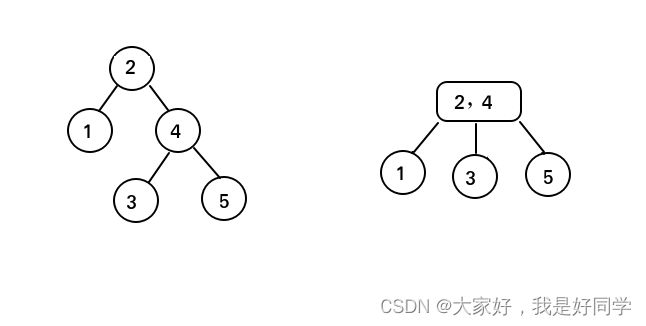
6. 插入一个值为6的新节点，直接将其插入将会作为5的右孩子，为了完美平衡，需要将新节点与值为5的节点进行融合，如下：
7. 插入一个值为7的节点，直接将其插入该新节点将会成为值位5，6的三节点的右孩子，为了得到完美平衡，我们将新节点与它的根结点（值为5，6的三节点）进行融合，如下图
但此时得到的四节点{5,6,7}不稳定，我们将其进行分解如下：
但是显然还是没有达到完美平衡，所以我们将递归检测得到的第一个不平衡的节点和其根结点进行融合，如下图：
此时我们的四节点{2,4,6}时不能存在的，四节点中值的大小关系和三节点中的关系很相似。
我们假设四节点的值分别为{key1, key2, key3}，那么该结点的四个子节点中的自左向右第一个节点小于key1，第二个节点中的值大于key1小于key2，第三个节点中的值大于key2小于key3，第四个节点中的值大于key3。
所以我们对其进行分解如下：
这样就得到了一棵完美平衡的二叉树了。
我们总结一下2-3查找树的插入策略：
- 根据查找树的插入原则先插入新节点；
- 若此时这个树没有完美平衡，则将新节点与其当前位置的根结点融合；
- 若此时得到一个四节点，则需要进行分解；
- 若此时查找树依旧没有完美平衡，则找到不平衡的节点进行融合；
- 循环3-4步骤，直至二叉树完美平衡。
这里需要注意分解节点的方式，当存在四节点需要分解且该四节点有孩子节点时，我们将需要根据我们在前文提到的节点值的大小关系进行分解。具体如图：
当四节点的位置不同，分解也有所差异i具体如下：
红黑树
基本定义
在《算法导论》和《算法》中对红黑树的定义是有所差别的，算法导论中的红黑树基于2-3-4查找数，算法中的红黑数基于2-3查找树。除此以外，这两种定义中对于颜色的表现对象是不同的，算法导论中节点根据所在位置的不同是不同颜色的，算法中是连接线根据其位置的不同是不同颜色的
我们接下来将主要学习《算法》中基于2-3查找树的红黑树，它的定义具体如下：
- 红色的线永远是左侧链接，这主要是为了处理方便。（强行的规定）
- 没有一个节点同时链了两条红色的线。（也就是没有4-node）
- 任何从根到叶子节点的路径上有相同数量颜色的黑线。(黑线节点完美平衡)
这里的红边意味着这个边连接的两个节点可以被融合在一起，可以将其看作时一个三节点，这样就将一棵2-3查找树表现成了一个二叉树，颜色信息将会被保存在节点信息中。
如下图所示：
也就是说红黑树其实就是模拟了一棵2-3查找树。
红黑树的平衡化
与AVL相同，红黑树也需要通过旋转保持平衡；不同的是旋转后，需要改变节点的颜色。我们知道红边连接的节点其实是被融合为了一个节点，所以这里需要注意的是，在红黑树中，树是由树根到叶子节点的路径上黑边的个数(黑节点个数)决定平衡。
旋转颜色变化规律：上升节点(旋转节点)变为原来父节点的颜色，下降节点变为红色。
左旋
实现代码如下：
Node* LeftRotate(Node* root){
Node* p = root;
Node* q = root->right;
Node* k = q->left;
p->right = k;
q->left = p;
q->color = p->color;
p->color = RED;
return q;
}
右旋
实现代码如下：
Node* RightRotate(Node* root){
Node* p = root;
Node* q = root->left;
Node* k = q->right;
q->right = p;
p->left = k;
q->color = p->color;
p->color = RED;
return q;
}
红黑树的插入
因为红黑树一定是一个完美平衡的二叉树，所以新插入一个结点一定会让这棵二叉树变得不平衡，也就是说新插入一个节点一定会进行一次融合，故而新插入的节点是红色的。接下来我们根据是插入进了一个二节点还是三节点的底部来分别讨论。
向2节点插入
如果新插入的节点是父节点的左子节点，那么就不需要进行旋转操作，直接插入即可，如下图：
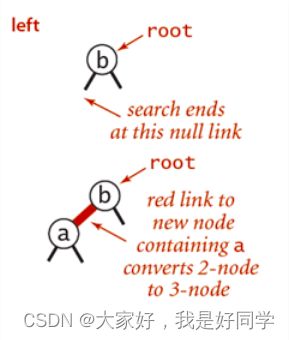
但是如果插入的节点时一个右子节点，那么需要将其旋转，确保红边位于左边，如下图所示：
向3节点插入
向一个3节点中插入新节点，有三种位置可以选择，如下：
若是插入第一个位置，也就是插入的节点比现有的两个节点都大，那么将会形成一个四节点，则需要进行分解，表现在红黑树上就是将节点上的颜色反转，如图：
若插入位置2，也就是插入的节点比现有的两个节点都小，形成了一个四节点，且此时需要对其进行右旋，且颜色反转，如下图所示：
如果插入第三个位置，也就是说插入的节点的值位于两个节点之间，这时需要对其进行左旋至情况二，此时采用情况二的处理方式即可，具体如下图所示：
我们总结一下插入的处理，对插入的数据进行分类，插入值为key，操作表格如下：
| key范围 | 操作 |
|---|---|
a| 颜色反转 |
|
key| b右旋(变成情况1)，然后颜色反转 |
|
a| a左旋(变成情况2)，b右旋(变成情况1)，然后颜色反转 |
|
在AVL树中，我们进行平衡化的时候，需要计算每一个节点的平衡因子，然后根据平衡因子来决定执行什么操作。但是在红黑树中我们直接根据节点的颜色来决定执行什么操作即可（在红黑树完成后每一个节点的平衡因子都为0）。
C++代码如下
void FlipColor(Node* node){ // 颜色反转
node->color = RED;
node->right->color = BLACK;
node->left->color = BLACK;
}
Node* Balanced(Node* root){
if(nullptr == root) return nullptr;
// 3节点插入红节点
// 红节点作为3节点的右节点插入
if(lsRed(root->left) && lsRed(root->right)){
FlipColor(root);
}
// 红节点作为3节点的左节点插入
else if(lsRed(root->left) && lsRed(root->left->left)){
root = RightRotate(root);
FlipColor(root);
}
// 红节点作为3节点的中间节点插入
else if(lsRed(root->left) && lsRed(root->left->right)){
root->left = LeftRotate(root)->left;
root = RightRotate(root);
FlipColor(root);
}
// 2节点插入红节点
else if(lsRed(root->right)){
root = LeftRotate(root); // 红节点作为右节点插入
}
return root;
}
我们可以对以上的代码进行优化，对以上的处理情况进行分类，代码如下：
Node* Balance(Node* root){
Node *res = root;
if (IsRed(root->right) and !IsRed(root->left)) // 如果节点的右子节点为红色，且左子节点位黑色，则进行左旋操作
res = LeftRotate(root);
if (IsRed(root->left) and IsRed(root->left->left)) // 如果节点的左子节点为红色，并且左子节点的左子节点也为红色，则进行右旋操作
res = RightRotate(root);
if (IsRed(root->left) and IsRed(root->right)) // 如果节点的左右子节点均为红色，则执行FlipColor操作，提升中间结点。
res = FlipColor(root);
return res;
}
红黑树的删除
红黑树的删除操作可以考虑为两部分，一部分为简单的查找删除，另一部分则是找到待删除节点后如何维持二叉树的平衡。
红黑树的删除与二叉搜索树BST的删除操作很相似，在BST中删除节点的时候将会遇到三种情况：
- 待删除节点是一个叶子结点
- 待删除节点有且只有一个子节点
- 待删除节点有两个子节点
我们对其的处理方式如下：
| 情况 | 处理方式 |
|---|---|
| 1 | 直接删除该节点 |
| 2 | 直接将该节点的唯一的子节点接到该节点的父节点上 ，删除该节点 |
| 3 | 找一个继承节点（因为寻找继承节点的方式导致了继承节点一定是情况1或者情况2），把继承节点的值写入p节点，根据情况1或者情况2来处理继承节点。 |
这个继承节点可以为该结点的右子树最小值或左子树最大值，此时就将删除节点的情况转换为情况1和情况2。
接下来就是如何进行平衡了，我们知道一棵红黑树的平衡取决于从根结点到叶子结点的黑色节点的个数是否相等。所以有两种情况是不需要进行平衡处理的，一是删除的是红色节点，二是删除的是根节点。
除了以上的两种情况，我们都需要在删除节点时对二叉树进行平衡操作，且这些节点都是黑节点，而且由于红黑树完美平衡的性质我们删除的节点（或者是我们找到的继承节点）一定是一个叶子节点，接下来根据待删除节点的兄弟节点颜色进行分类处理，如下：
- 情况一： 兄弟节点是红节点
在这种情况下他们的父节点一定不是红节点，并且兄弟节点的左孩子和右孩子必然是黑节点，如图所示：
删除待删除节点，得到如下图：
我们将父节点变红，兄弟节点变黑，对其进行左旋。从而进行平衡，如下图：
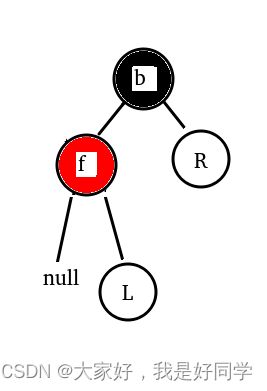
- 情况二： 兄弟节点是黑节点
根据兄弟节点的子节点颜色对情况二进行分类处理，如下表所示：
| 具体情况 | 处理 |
|---|---|
| 都是黑节点 | 将同级的兄弟节点变红 |
| 左红右黑 | 将红节点转为右孩子，使用【左黑又红】的情况继续进行处理 |
| 左黑右红 | 将右孩子变为黑色，兄弟节点和其父节点颜色交换，以其父节点为根结点的树进行左旋 |
注意：为什么要求右孩子是红色？
我们平衡的思路时将根结点左旋到待删除节点的那颗子树上去，补充本被删除的黑节点数目，这样兄弟节点将会作为根结点，所以缺少一个节点的子树变成了兄弟节点的右子树，如果我们保证兄弟节点的右孩子是一个红节点，这时将这个红节点转换为黑节点作为右子树上的补充，就可以成功的达到平衡了。
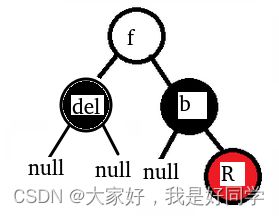
以上这三种方式中第三种情况不是很好理解，我们图解一下第三种情况的处理方式，如下图所示存在一个这样的待删除节点：
我们删除del节点，如下图：
这显然是不平衡的，我们首先转变节点颜色，将红色的右孩子节点转换为黑色节点，作为之后左旋的右子树中缺少的节点预备补充，如下图所示：
我们对其进行左旋，平衡化结束，如下图：
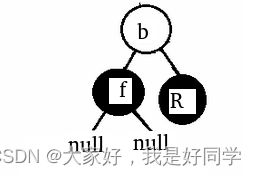
以上就是红黑树中删除节点的全部思路了，具体代码如下：
Node* RemoveNode(Node*& node, int key) {
Node* res = NULL;
if(NULL == node) return NULL;
if (key < node->key) { // 左子树
if(!IsRed(node->left) && !IsRed(node->left->left)) node = MoveRedLeft(node);
node->left = RemoveNode(node->left, key);
} else if(key > node->key) {
if(IsRed(node->left)) node = RightRotate(node);
if(!IsRed(node->right) && !IsRed(node->right->left)) node = MoveRedRight(node);
node->right = RemoveNode(node->right,key);
} else if(key == node->key) {
if(IsLeaf(node) && IsRed(node)) {
delete node;
return NULL;
}
// #define DELETE_MIN
#ifdef DELETE_MIN
if(IsRed(node->left)) node = RightRotate(node);
if(!IsRed(node->right) && !IsRed(node->right->left)) node = MoveRedRight(node);
if(key == node->key) { // 借不到的情况
Node* p = Minimum(node->right);
node->key = p->key;
node->right = RemoveNode(node->right,p->key);
} else {
node->right = RemoveNode(node->right,key);
}
#else
if(!IsRed(node->left) && !IsRed(node->left->left)) node = MoveRedLeft(node);
if(key == node->key) { // 借不到的情况
Node* p = Maximum(node->left);
node->key = p->key;
node->left = RemoveNode(node->left,p->key);
} else {
node->left = RemoveNode(node->left, key);
}
#endif
}
return Balance(node); // 平衡
}
// 删除
Node* Remove(Node*& node,int key){
if(!IsRed(node->right) && !IsRed(node->left)) // 根节点左右子树不为黑节点
node->color = RED; // 根节点暂时变为红节点
node = RemoveNode(node,key);
if(NULL != node) node->color = BLACK;
return node;
}