力扣刷题(代码回忆录)——单调栈部分
- 单调栈:每日温度
- 单调栈:下一个更大元素I
- 单调栈:下一个更大元素II
- 单调栈:接雨水
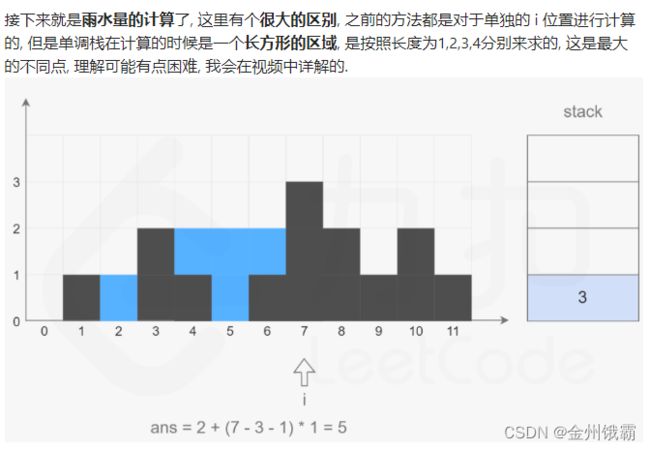
- 单调栈:柱状图中最大的矩形
单调栈总结
单调递增栈:从 栈底 到 栈顶 递增,栈顶大
单调递减栈:从 栈底 到 栈顶 递减,栈顶小
1:什么时候使用单调栈?
通常是一维数组,要寻找任一元素右边(左边)第一个比自己大(小)的元素,且要求 O(n) 的时间复杂度
2:模板套路
1): 当前项向右找第一个比自己大的位置 —— 从右向左维护一个单调递减栈
def nextGreaterElement_01(nums: list):
length = len(nums)
res, stack = [-1] * length, []
for i in range(length - 1, -1, -1):
while stack and stack[-1] <= nums[i]:
stack.pop()
if stack:
res[i] = stack[-1]
stack.append(nums[i])
return res
- 或者 当前项向右找第一个比自己大的位置 —— 从左向右维护一个单调递减栈
def nextGreaterElement_011(nums: list):
length = len(nums)
res, stack = [-1] * length, []
for i in range(length):
while stack and nums[stack[-1]] < nums[i]:
idx = stack.pop()
res[idx] = nums[i]
stack.append(i)
return res
2):当前项向右找第一个比自己小的位置 —— 从右向左维护一个单调递增栈
def nextGreaterElement_02(nums: list):
length = len(nums)
res, stack = [-1] * length, []
for i in range(length - 1, -1, -1):
while stack and stack[-1] >= nums[i]:
stack.pop()
if stack:
res[i] = stack[-1]
stack.append(nums[i])
return res
3): 当前项向左找第一个比自己大的位置 —— 从左向右维护一个单调递减栈
def nextGreaterElement_03(nums: list):
length = len(nums)
res, stack = [-1] * length, []
for i in range(length):
while stack and stack[-1] <= nums[i]:
stack.pop()
if stack:
res[i] = stack[-1]
stack.append(nums[i])
return res
4): 当前项向左找第一个比自己小的位置 —— 从左向右维护一个单调递增栈
def nextGreaterElement_04(nums: list):
length = len(nums)
res, stack = [-1] * length, []
for i in range(length):
while stack and stack[-1] >= nums[i]:
stack.pop()
if stack:
res[i] = stack[-1]
stack.append(nums[i])
return res
739. 每日温度
给定一个整数数组 temperatures ,表示每天的温度,返回一个数组 answer ,其中 answer[i] 是指对于第 i 天,下一个更高温度出现在几天后。如果气温在这之后都不会升高,请在该位置用 0 来代替。
示例 1:
输入:temperatures = [73,74,75,71,69,72,76,73]
输出: [1,1,4,2,1,1,0,0]示例 2:
输入: temperatures = [30,40,50,60]
输出: [1,1,1,0]示例 3:
输入: temperatures = [30,60,90]
输出: [1,1,0]提示:
1 <= temperatures.length <= 10530 <= temperatures[i] <= 100
算法思想:
实现代码:
这道题的关键是:用栈记录的是list中元素的index,而不是list中元素值本身。后面在操作stack时,操作的都是index,这样就能实现把ans中对应位置给替换掉的效果。
class Solution:
def dailyTemperatures(self, temperatures: List[int]) -> List[int]:
stack, ans =[], [0 for _ in range(len(temperatures))]#stack用来存储temperatures的元素下标的
for i in range(len(temperatures)):#采用单调递减栈,每次有较大的数入栈,都需要将之前的数都弹出
while(stack and temperatures[stack[-1]] < temperatures[i]):
index = stack.pop()#记录弹出元素的下标(每一个下标对应一个元素)
ans[index] = i - index#i指向当前的数是第一个大于index指向的数
stack.append(i)
return ans
496. 下一个更大元素 I
nums1 中数字 x 的 下一个更大元素 是指 x 在 nums2 中对应位置 右侧 的 第一个 比 x 大的元素。
给你两个 没有重复元素 的数组 nums1 和 nums2 ,下标从 0 开始计数,其中nums1 是 nums2 的子集。
对于每个 0 <= i < nums1.length ,找出满足 nums1[i] == nums2[j] 的下标 j ,并且在 nums2 确定 nums2[j] 的 下一个更大元素 。如果不存在下一个更大元素,那么本次查询的答案是 -1 。
返回一个长度为 nums1.length 的数组 ans 作为答案,满足 ans[i] 是如上所述的 下一个更大元素 。
示例 1:
输入:nums1 = [4,1,2], nums2 = [1,3,4,2].
输出:[-1,3,-1]
解释:nums1 中每个值的下一个更大元素如下所述:
- 4 ,用加粗斜体标识,nums2 = [1,3,4,2]。不存在下一个更大元素,所以答案是 -1 。
- 1 ,用加粗斜体标识,nums2 = [1,3,4,2]。下一个更大元素是 3 。
- 2 ,用加粗斜体标识,nums2 = [1,3,4,2]。不存在下一个更大元素,所以答案是 -1 。示例 2:
输入:nums1 = [2,4], nums2 = [1,2,3,4].
输出:[3,-1]
解释:nums1 中每个值的下一个更大元素如下所述:
- 2 ,用加粗斜体标识,nums2 = [1,2,3,4]。下一个更大元素是 3 。
- 4 ,用加粗斜体标识,nums2 = [1,2,3,4]。不存在下一个更大元素,所以答案是 -1 。提示:
1 <= nums1.length <= nums2.length <= 10000 <= nums1[i], nums2[i] <= 104nums1和nums2中所有整数 互不相同nums1中的所有整数同样出现在nums2中
算法思想:
从左到右维护单调递减栈,每次有比自己大的元素在栈里就把他们全部弹出 。
因为nums1是nums2的子集,所以我们只需要将nums2中下一个更大元素结果全部求出来。然后nums1的结果在字典序d中没有键值对的,我们将它赋予-1,最后存到一个数组ans里输出。
实现代码:
class Solution:
def nextGreaterElement(self, nums1: List[int], nums2: List[int]) -> List[int]:
d, ans = {}, []#d用来存储nums2中下一个更大元素结果的键值对
#因为nums1是nums2的子集,所以我们只需要将nums2中下一个更大元素结果全部求出来
#然后nums1的结果再d中没有键值对的,我们将它赋予-1
stack = []#维护一个单调递减栈
for i in range(len(nums2)):
while(stack and stack[-1] < nums2[i]):#把栈里小于nums2[i]全部弹出
d[stack.pop()] = nums2[i]#记录nums2中下一个更大元素
stack.append(nums2[i])
for i in range(len(nums1)):
ans.append(d.get(nums1[i], -1))
return ans
# dict.get(key, default=None)
# key -- 字典中要查找的键。
# default -- 如果指定键的值不存在时,返回该默认值default。503. 下一个更大元素 II(这题单调栈比较典型,需要记住代码模板)
给定一个循环数组 nums ( nums[nums.length - 1] 的下一个元素是 nums[0] ),返回 nums 中每个元素的 下一个更大元素 。
数字 x 的 下一个更大的元素 是按数组遍历顺序,这个数字之后的第一个比它更大的数,这意味着你应该循环地搜索它的下一个更大的数。如果不存在,则输出 -1 。
示例 1:
输入: nums = [1,2,1]
输出: [2,-1,2]
解释: 第一个 1 的下一个更大的数是 2;
数字 2 找不到下一个更大的数;
第二个 1 的下一个最大的数需要循环搜索,结果也是 2。示例 2:
输入: nums = [1,2,3,4,3]
输出: [2,3,4,-1,4]提示:
1 <= nums.length <= 104-109 <= nums[i] <= 109
算法思想:
同496. 下一个更大元素 I这题一样,只不过这题加了循环数组,所以需要对遍历下标取mod即i%len(nums)。
实现代码:
class Solution:
def nextGreaterElements(self, nums: List[int]) -> List[int]:
stack, ans = [], [-1 for _ in range(len(nums))]#stack存num里数的下标
for i in range(len(nums)*2):
while(stack and nums[stack[-1]] < nums[i%len(nums)]):#维护一个单调递减栈
ans[stack.pop()] = nums[i%len(nums)]
stack.append(i%len(nums))#因为下标唯一且数不唯一,所以选择将数组下标压入栈中
return ans42. 接雨水
给定 n 个非负整数表示每个宽度为 1 的柱子的高度图,计算按此排列的柱子,下雨之后能接多少雨水。
算法思想:参考:力扣
本题设计的是一个单调递减栈: 维护一个单调栈, 单调栈存储的是下标, 满足从栈底到栈顶的下标对应的数组 height 中的元素递减.
我们来分析下单调栈为什么可以满足此题的要求. 首先明确一点: 只有产生凹陷的地方才能存储雨水, 那么高度一定是先减后增, 所以当我们遍历到 增 这个位置的时候, 前面的减的地方(凹陷处-即height数组先减后增)一定会存储雨水, 所以我们就将凹陷处出栈, 来计算它所能存储的雨水量.
用算法思想来表述就是: 从左到右遍历数组, 遍历到下标 i 时, 如果栈内至少有两个元素, 记栈顶元素为top, top 的下面一个元素是 left, 则一定有height[left]≥height[top]。如果height[i]>height[top], 则得到一个可以接雨水的区域.
该区域的宽度是i−left−1, 高度是min(height[left],height[i])−height[top], 根据宽度和高度即可计算得到该区域能接的雨水量.
在代码中有一个要注意的点: 就是弹出栈顶后判断栈是否为空, 因为当栈为空, 说明左边不存在最大值, 是无法接雨水的.
实现代码:
class Solution:
def trap(self, height: List[int]) -> int:
stack, sum = [], 0
for i in range(len(height)):
while(stack and height[stack[-1]] < height[i]):
top = stack.pop()
if(not stack):#有凹陷区域,所以栈中必须要有两个元素
break
left = stack[-1]#指向栈顶元素的下一个元素
w = i - left - 1#雨水的宽度
h = min(height[left], height[i]) - height[top]#雨水的宽度
sum += w * h
stack.append(i)
return sum