算法设计与分析期末复习题
一. 选择题
1.Hanoi塔问题如下图所示。现要求将塔座A上的的所有圆盘移到塔座B上,并仍按同样顺序叠置。移动圆盘时遵守Hanoi塔问题的移动规则。由此设计出解Hanoi塔问题的递归算法正确的为:(B)

4. 算法分析中,记号O表示(B ), 记号 表示(A ), 记号 表示(D)。
A.渐进下界
B.渐进上界
C.非紧上界
D.紧渐进界
E.非紧下界
- 以下关于渐进记号的性质是正确的有:( A)
A.
B.
C. O(f(n))+O(g(n)) = O(min{f(n),g(n)})
D.
4 程序块( A)是回溯法中遍历排列树的算法框架程序。
A.
void backtrack (int t)
{
if (t>n) output(x);
else
for (int i=t;i<=n;i++) {
swap(x[t], x[i]);
if (legal(t)) backtrack(t+1);
swap(x[t], x[i]);
}
}
B.
void backtrack (int t)
{
if (t>n) output(x);
else
for (int i=0;i<=1;i++) {
x[t]=i;
if (legal(t)) backtrack(t+1);
}
}
C
void backtrack (int t)
{
if (t>n) output(x);
else
for (int i=0;i<=1;i++) {
x[t]=i;
if (legal(t)) backtrack(t-1);
}
}
D
void backtrack (int t)
{
if (t>n) output(x);
else
for (int i=t;i<=n;i++) {
swap(x[t], x[i]);
if (legal(t)) backtrack(t+1);
}
}
5 动态规划算法的基本要素为( C)
A. 最优子结构性质与贪心选择性质
B.重叠子问题性质与贪心选择性质
C.最优子结构性质与重叠子问题性质
D. 预排序与递归调用
6 从活结点表中选择下一个扩展结点的不同方式将导致不同的分支限界法,以下除( C)之外都是最常见的方式。
A.队列式分支限界法
B.优先队列式分支限界法
C.栈式分支限界法
D.FIFO 分支限界法
7下面关于矩阵乘法的 Stranssen 算法,描述错误的是(D )。
A. 采用了分治法的思想
B. 时间复杂度低于 O(n3)
C. 利用了分块矩阵乘法
D. 对所有可乘的矩阵都适用
8、 分支限界法与回溯法都是在问题的解空间树 T 上搜索问题的解,二者(B)。
A.求解目标不同,搜索方式相同
B.求解目标不同,搜索方式也不同
C.求解目标相同,搜索方式不同
D.求解目标相同,搜索方式也相同
9、回溯法的效率不依赖于以下哪一个因素?( C)
A. 产生x[k]的时间;
B. 满足显约束的x[k]值的个数;
C. 问题的解空间的形式;
D. 计算上界函数bound的时间;
E. 满足约束函数和上界函数约束的所有x[k]的个数。
F. 计算约束函数constraint的时间;
二.填空题
1、选择排序、插入排序和合并排序算法中,( 合并)算法是分治算法。
2、分治算法的时间复杂性常常满足如下形式的递归方程:
其中,g(n)表示( 将规模为n的问题分解为子问题以及组合相应的子问题的解所需的时间)。
3、程序是算法的具体实现,程序可以不满足算法的( )性质。
4、决定算法复杂性的因素主要有 (求解问题的规模 )、(具体的输入数据 )和 (算法本身的设计 )。
5、函数 n3 /10+3n 的渐进表达式为(O(n3),函数log 3 + 10 log 3的渐进表达式为 ( O(1))。
6、快速排序和合并排序策略上是相同的,都是用的(分治 ) 算法。
7、求最小生成树的 Prim 算法和 Kruskal 算法本质上都是(贪心)算法。
8、概率算法是一种非确定性地选择下一计算步骤的方法,(拉斯维加斯算法)算法不一定能得到解,但得到的一定是正确解,( 舍伍德算法)算法主要目的是消除算法所需计算时间对输入实例的依赖。
9、下面程序段的所需要的计算时间为( O(n2) )。
int MaxSum(int n, int *a, int &besti, int &bestj)
{
int sum=0;
for(int i=1;i<=n;i++){
int thissum=0;
for(int j=i;j<=n;j++){
thissum+=a[j];
if(thissum>sum) {
sum=thissum;
besti=i;
bestj=j;
}
}
}
return sum;
}
10、在深度神经网络中,前向传播输出的是(预测结果),反向传播是(更新参数/计算梯度),卷积适合(网格化)数据。
11、算法的复杂性等于(算法所需的计算资源)。
12、在忽略常数因子的情况下,O、 和 三个符号中,(O )提供了算法运行时间的一个上界。
13、设Dn表示大小为n的输入集合,t(I)表示输入为I时算法的运算时间, p(I)表示输入I出现的概率,则算法的平均情况下时间复杂性A(n)= ( ) 。
14、动态规划和分治法在分解子问题方面的不同点是( )。
三.简答题
1、简单描述分治法、动态规划法、贪心算法的基本思想。
2、何谓最优子结构性质?
3、何谓P、NP问题
4、最坏情况下的时间复杂性和平均时间复杂性有什么不同?
5、回溯法的搜索特点是什么,其显著特性是什么?
6、二分检索算法最多的比较次数?
7、算法重要特性是什么? 算法分析的目的是什么?算法的时间复杂性与问题的什么因素相关?算法的渐进时间复杂性的含义?最坏情况下的时间复杂性和平均时间复杂性有什么不同?
四.计算题
1、1、有11个待安排的活动,它们具有下表所示的开始时间与结束时间,如果以贪心算法求解这些活动的最优安排(即为活动安排问题:在所给的活动集合中选出最大的相容活动子集合),得到的最大相容活动子集合为活动({1,4,8,11})。

2、已知非齐次递归方程: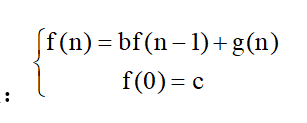
,其中,b、c是常数,g(n)是n的某一个函数。则f(n)的非递归表达式为: 
现有Hanoi塔问题的递归方程为:
,求h(n)的非递归表达式。
b=2,c =1,g(n)=1
3、下面是一个递归算法,其中,过程pro1和pro2的运算时间分别是1和 。给出该算法的时间复杂性T(n)满足的递归方程,并求解该递归方程,估计T(n)的阶(用 表示)。
算法 EX1 输入:正整数n,n=2k。输出:…
if (n=1)
pro1(n)
else
pro2(n)
ex1(n/2)
return
T(n)=
五.算法求解题
1、单源最短路径的求解。
问题的描述:给定带权有向图(如下图所示)G =(V,E),其中每条边的权是非负实数。另外,还给定V中的一个顶点,称为源。现在要计算从源到所有其它各顶点的最短路长度。这里路的长度是指路上各边权之和。这个问题通常称为单源最短路径问题。
解法:现采用Dijkstra算法计算从源顶点1到其它顶点间最短路径。请将此过程填入下表中。

2、写出多段图最短路经动态规划算法求解下列实例的过程,并求出最优值。
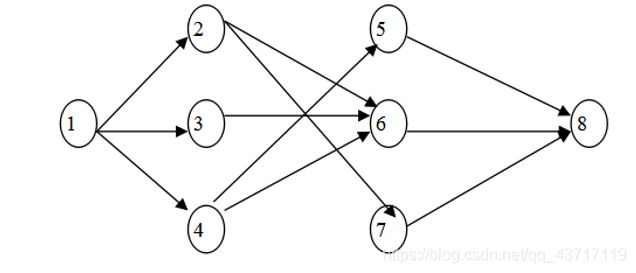
各边的代价如下:
C(1,2)=3, C(1,3)=5 ,C(1,4)=2
C(2,6)=8,C(2,7)=4 ,C(3,5)=5 ,C(3,6)=4, C(4,5)=2,C(4,6)=1
C(5,8)=4, C(6,8)=5 ,C(7,8)=6
C(5,8)=4, C(6,8)=5, C(7,8)=6
C(2,8)= min(C(2,6)+C(6,8) C(2,7)+C(7,8))=
C(3,8)= min()
C(4,8)=
C(1,8)=
3、设有n=2k个运动员要进行循环赛,现设计一个满足以下要求的比赛日程表:
①每个选手必须与其他n-1名选手比赛各一次;
②每个选手一天至多只能赛一次;
③循环赛要在最短时间内完成。
(1)如果n=2k,循环赛最少需要进行几天;
(2)当n=23=8时,请画出循环赛日程表。
4、设MC(x)是一个一致的75%正确的蒙特卡罗算法,考虑下面的算法:
MC3(x) {
t=MC(x);
u=MC(x);
v=MC(x);
if ((tu)||(tv)) return t;
return v;}
求算法MC3(x)的正确率。
000 001 010 011 100 101 110 111
25%*75%*75%+75%*25%*75%+75%*75%*25%+75%*75%*75%=
5、假设有5个物品,它们的重量和价值如下表所示。若这些物品均不能被分割,且背包容量M=100,使用回溯方法求解此背包问题。请写出状态空间搜索树。
物品 A B C D E
重量 35 30 60 50 40
价值 10 40 30 50 35
六、算法设计题
1、一个旅行者要驾车从A地到B地,A、B两地间距离为s。A、B两地之间有n个加油站,已知第i个加油站离起点A的距离为 公里,0= ,车加满油后可行驶m公里,出发之前汽车油箱为空。应如何加油使得从A地到B地沿途加油次数最少?给出用贪心法求解该最优化问题的贪心选择策略,写出求该最优化问题的最优值和最优解的贪心算法,并分析算法的时间复杂性。
算法 MINSTOPS
输入:A、B两地间的距离s,A、B两地间的加油站数n,车加满油后可行驶的公里数m,存储各加油站离起点A的距离的数组d[1…n]。
输出:从A地到B地的最少加油次数k以及最优解x[1…k](x[i]表示第i次加油的加油站序号),若问题无解,则输出no
solution。
d[n+1]=s; //设置虚拟加油站第n+1站。
for i=1 to n
if d[i+1]-d[i]>m then
output “no solution”; return //无解,返回
end if
end for
k=1; x[k]=1 //在第1站加满油。
s1=m //s1为用汽车的当前油量可行驶至的地点与A点的距离
i=2
while s1<s
if d[i+1]>s1 then //以汽车的当前油量无法到达第i+1站。
k=k+1; x[k]=i //在第i站加满油。
s1=d[i]+m //刷新s1的值
end if
i=i+1
end while
output k, x[1..k]
MINSTOPS
最坏情况下的时间复杂性:Θ(n)
2、回溯法、分支限界法求解作业调度问题
3、关于TSP问题的各种解法
补充填空题
1、所谓贪心选择性质是指(所求问题的整体最优解可以通过一系列局部最优的选择,即贪心选择来达到)。
2、所谓最优子结构性质是指(问题的最优解包含了其子问题的最优解)。
3、回溯法是回溯法是指(具有限界函数的深度优先生成法)。
4、用回溯法解题的一个显著特征是在搜索过程中动态产生问题的解空间。在任何时刻,算法只保存从根结点到当前扩展结点的路径。如果解空间树中从根结点到叶结点的最长路径的长度为h(n),则回溯法所需的计算空间通常为(O(h(n))
)。
5、 回溯法的算法框架按照问题的解空间一般分为(子集树)算法框架与(排列树)算法框架。
6、用回溯法解0/1背包问题时,该问题的解空间结构为(子集树)结构。
7、用回溯法解批处理作业调度问题时,该问题的解空间结构为(排列树)结构。
