二维前缀和数组&二维差分数组
二维前缀和数组&二维差分数组
一维前缀和
-
用途:快速求出数组中 n u m s [ i , j ] nums[i,j] nums[i,j]元素之和
-
定义: s u m s [ i + 1 ] sums[i+1] sums[i+1]为
nums数组前 i i i个元素之和
s u m s [ i + 1 ] = ∑ j = 0 i n u m s [ j ] sums[i + 1] = \sum _{j=0} ^{i}nums[j] sums[i+1]=j=0∑inums[j] -
因此,可以快速计算出数组中 n u m s [ i , j ] nums[i,j] nums[i,j]元素之和为 s u m [ j + 1 ] − s u m [ i ] sum[j+1]-sum[i] sum[j+1]−sum[i]
一维差分
-
定义:差分数组的每一项都是原数组该项与上一项的差
d [ i ] = a [ i ] − a [ i − 1 ] d[i]=a[i]-a[i-1] d[i]=a[i]−a[i−1] -
用途:常用于区间修改,如对原始数组a[n]内一段区间上的数值进行加减操作,则:
- 在差分数组d[n]选定区间[l,r],确认加减数值x
d [ l ] + = x d [ r + 1 ] − = x d[l] += x \\d[r+1] -= x d[l]+=xd[r+1]−=x
- 然后对该数组求累加和数组,就得到了变化后的数组
-
例如
index 0 1 2 3 4 5 原始数组 0 2 3 7 5 8 原差分数组 0 2 1 4 -2 3 操作:对区间[1,3]+3 5 6 10 现差分数组 0 5 1 4 -5 3 累加和数组 0 5 6 10 5 8
二维前缀和
-
「二维前缀和」解决的是二维矩阵中的矩形区域求和问题。
-
二维前缀和数组中的每一个格子记录的是「**以当前位置为区域的右下角(区域左上角恒定为原数组的左上角)**的区域和」【应该不固定 可以倒转】
s u m [ i , j ] = s u m [ i − 1 ] [ j ] + s u m [ i ] [ j − 1 ] − s u m [ i − 1 ] [ j − 1 ] + m a t r i x [ i ] [ j ] sum[i,j] = sum[i-1][j]+sum[i][j-1]-sum[i-1][j-1]+matrix[i][j] sum[i,j]=sum[i−1][j]+sum[i][j−1]−sum[i−1][j−1]+matrix[i][j]

-
因此,如果要求 (x1, y1) 作为左上角,(x2, y2) 作为右下角的区域和的时候,可以直接利用二维前缀和数组快速求解:
r e s = s u m [ x 2 ] [ y 2 ] − s u m [ x 1 − 1 ] [ y 2 ] − s u m [ x 2 ] [ y 1 − 1 ] + s u m [ x 1 − 1 ] [ y 1 − 1 ] res=sum[x2][y2] - sum[x1 - 1][y2] - sum[x2][y1 - 1] + sum[x1 - 1][y1 - 1] res=sum[x2][y2]−sum[x1−1][y2]−sum[x2][y1−1]+sum[x1−1][y1−1]
二维差分
-
「二维差分」解决的是二维矩阵中的矩形区域值的变化问题。
-
两种情况:以当前位置为左上角或右下角
-
左上角
-
二维数组某个位置 ( x 1 , y 1 ) (x1,y1) (x1,y1)的变化量,可由二维差分数组的二维前缀和数组得到,即以当前位置为左上角,原数组的右下角为右下角的区域和
-
二维差分数组中的每一个格子记录的是「以当前位置为区域的右下角(区域左上角恒定为原数组的左上角)的值的变化量」【应该不固定 可以倒转】
-
因此,如果要求 ( x 1 , y 1 ) (x1, y1) (x1,y1) 作为左上角, ( x 2 , y 2 ) (x2, y2) (x2,y2) 作为右下角的区域值增加 x x x的时候,可以利用二维差分数组快速求解,此时相当于二维差分矩阵上对 ( x 2 , y 2 ) (x2,y2) (x2,y2)增加 x x x,对 ( x 2 , y 1 − 1 ) (x2,y1-1) (x2,y1−1)和 ( x 1 − 1 , y 2 ) (x1-1,y2) (x1−1,y2)减小 x x x,再对重复区域 ( x 1 − 1 , y 1 − 1 ) (x1-1,y1-1) (x1−1,y1−1)增加 x x x
-
二维数组某个位置 ( x 1 , y 1 ) (x1,y1) (x1,y1)的变化量,可由二维差分数组的二维前缀和数组
sum得到,即以当前位置为左上角,原数组的右下角为右下角的区域和【倒叙求】
s u m [ i , j ] = s u m [ i + 1 ] [ j ] + s u m [ i ] [ j + 1 ] − s u m [ i + 1 ] [ j + 1 ] + d e v [ i ] [ j ] sum[i,j] = sum[i+1][j]+sum[i][j+1]-sum[i+1][j+1]+dev[i][j] sum[i,j]=sum[i+1][j]+sum[i][j+1]−sum[i+1][j+1]+dev[i][j]
-
-
右下角【常用】
-
二维数组某个位置 ( x 1 , y 1 ) (x1,y1) (x1,y1)的变化量,可由二维差分数组的二维前缀和数组得到,即以当前位置为右下角,原数组的左上角为左上角的区域和
-
二维差分数组中的每一个格子记录的是「以当前位置为区域的左上角(区域右下角恒定为原数组的右下角)的值的变化量」【应该不固定 可以倒转】
-
因此,如果要求 ( x 1 , y 1 ) (x1, y1) (x1,y1) 作为左上角, ( x 2 , y 2 ) (x2, y2) (x2,y2) 作为右下角的区域值增加 x x x的时候,可以利用二维差分数组快速求解,此时相当于二维差分矩阵上对 ( x 1 , y 1 ) (x1,y1) (x1,y1)增加 x x x,对 ( x 2 + 1 , y 1 ) (x2+1,y1) (x2+1,y1)和 ( x 1 , y 2 + 1 ) (x1,y2+1) (x1,y2+1)减小 x x x,再对重复区域 ( x 2 + 1 , y 2 + 1 ) (x2+1,y2+1) (x2+1,y2+1)增加 x x x
-
要求得二维数组每个位置 ( x 1 , y 1 ) (x1,y1) (x1,y1)的变化量,即求二维差分数组的二维前缀和数组
sum,即差分数组以当前位置为右下角,原数组的左上角为左上角的区域和
s u m [ i , j ] = s u m [ i − 1 ] [ j ] + s u m [ i ] [ j − 1 ] − s u m [ i − 1 ] [ j − 1 ] + d e v [ i ] [ j ] sum[i,j] = sum[i-1][j]+sum[i][j-1]-sum[i-1][j-1]+dev[i][j] sum[i,j]=sum[i−1][j]+sum[i][j−1]−sum[i−1][j−1]+dev[i][j]
-
-
总结
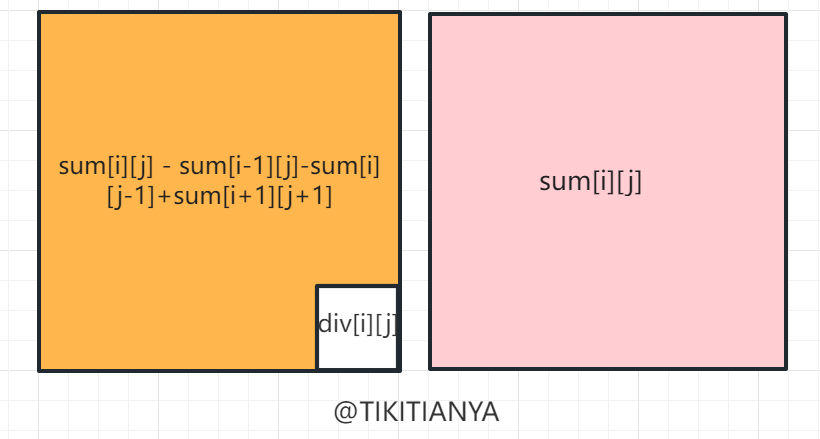
- 二维差分数组可视为以位置[i,j]为右下角原点为右上角的区域之和【二维前缀和数组 s u m [ i ] [ j ] sum[i][j] sum[i][j]】与该区域除了位置[i,j]的区域和之差,用二维前缀和数组可表示为
d i v [ i ] [ j ] = s u m [ i ] [ j ] − s u m [ i − 1 ] [ j ] − s u m [ i ] [ j − 1 ] + s u m [ i + 1 ] [ j + 1 ] div[i][j]=sum[i][j] - sum[i-1][j]-sum[i][j-1]+sum[i+1][j+1] div[i][j]=sum[i][j]−sum[i−1][j]−sum[i][j−1]+sum[i+1][j+1]
- 因此若已知二维数组a,求得其二维前缀和数组b,那么a即为b的差分数组
-
用途:将某一区域的值进行变化,首先求出差分数组,然后对该求出二维前缀和数组,即可求得变化后的结果
-
模板:由区域变化量求得二维差分数组,由二维差分数组求前缀和数组
二维差分数组div中的每一个格子记录的是「以当前位置为区域的左上角(区域右下角恒定为原数组的右下角)的值的变化量」【应该不固定 可以倒转】
二维差分数组的二维前缀和数组
sum,即差分数组以当前位置为右下角,原数组的左上角为左上角的区域和-
初始时div数组需要扩展边界,转化为
sum时需要处理0class Solution { public int[][] rangeAddQueries(int n, int[][] queries) { int[][] div = new int[n + 1][n + 1]; for (int[] q : queries){ div[q[0]][q[1]]++; div[q[0]][q[3] + 1]--; div[q[2] + 1][q[1]]--; div[q[2] + 1][q[3] + 1]++; } int[][] sum = new int[n][n]; for (int i = 0; i < n; i++){ for (int j = 0; j < n; j++){ sum[i][j] = div[i][j]; if (i != 0) sum[i][j] += sum[i - 1][j]; if (j != 0) sum[i][j] += sum[i][j - 1]; if (i != 0 && j != 0) sum[i][j] -= sum[i - 1][j - 1]; } } return sum; } } -
div数组边界可以+2,方便处理0
d i v [ 1 : n ] [ 1 : n ] div[1:n][1:n] div[1:n][1:n]计算为二维前缀和数组,在赋值给结果集
class Solution { public int[][] rangeAddQueries(int n, int[][] queries) { int[][] div = new int[n + 2][n + 2]; for (int[] q : queries){ div[q[0] + 1][q[1] + 1]++; div[q[0] + 1][q[3] + 2]--; div[q[2] + 2][q[1] + 1]--; div[q[2] + 2][q[3] + 2]++; } int[][] sum = new int[n][n]; for (int i = 1; i <= n; i++){ for (int j = 1; j <= n; j++){ sum[i - 1][j - 1] = (div[i][j] += div[i - 1][j] + div[i][j - 1] - div[i - 1][j - 1]); } } return sum; } }
-
-
模板:由前缀和数组求得二维差分数组即求出每个位置的数值
// sum n*n // div (n+1)*(n+1) //求出差分数组 for(int i=1;i<=n;i++) for(int j=1;j<=m;j++){ div[i][j]=sum[i][j]-sum[i-1][j]-sum[i][j-1]+sum[i-1][j-1]; }
相关题目
子矩阵元素加 1【LC2536】
给你一个正整数
n,表示最初有一个n x n、下标从 0 开始的整数矩阵mat,矩阵中填满了 0 。另给你一个二维整数数组
query。针对每个查询query[i] = [row1i, col1i, row2i, col2i],请你执行下述操作:
- 找出 左上角 为
(row1i, col1i)且 右下角 为(row2i, col2i)的子矩阵,将子矩阵中的 每个元素 加1。也就是给所有满足row1i <= x <= row2i和col1i <= y <= col2i的mat[x][y]加1。返回执行完所有操作后得到的矩阵
mat。
暴力
java过了…
class Solution {
public int[][] rangeAddQueries(int n, int[][] queries) {
int[][] mat = new int[n][n];
for (int[] query : queries){
int row1 = query[0], col1 = query[1], row2 = query[2], col2 = query[3];
for (int i = row1; i <= row2; i++){
for (int j = col1; j <= col2; j++){
mat[i][j]++;
}
}
}
return mat;
}
}
- 复杂度
- 时间复杂度: O ( n 2 ∗ q ) O(n^2*q) O(n2∗q), q q q为 q u e r i e s queries queries的长度
- 空间复杂度: O ( 1 ) O(1) O(1)
二维差分
前置知识:二维差分数组与二维前缀和数组
-
思路:使用二维差分数组记录每个区域的变化量,然后通过二维前缀和数组求得每个位置的值
-
实现
-
二维差分数组
div中的每一个格子记录的是「以当前位置为区域的左上角(区域右下角恒定为原数组的右下角)的值的变化量」【应该不固定 可以倒转】 -
二维差分数组的二维前缀和数组
sum,即差分数组以当前位置为右下角,原数组的左上角为左上角的区域和 -
因此,如果要求 ( x 1 , y 1 ) (x1, y1) (x1,y1) 作为左上角, ( x 2 , y 2 ) (x2, y2) (x2,y2) 作为右下角的区域值增加 x x x的时候,可以利用二维差分数组快速求解,此时相当于二维差分矩阵上对 ( x 1 , y 1 ) (x1,y1) (x1,y1)增加 x x x,对 ( x 2 + 1 , y 1 ) (x2+1,y1) (x2+1,y1)和 ( x 1 , y 2 + 1 ) (x1,y2+1) (x1,y2+1)减小 x x x,再对重复区域 ( x 2 + 1 , y 2 + 1 ) (x2+1,y2+1) (x2+1,y2+1)增加 x x x
-
要求得二维数组每个位置 ( x 1 , y 1 ) (x1,y1) (x1,y1)的变化量,即求二维差分数组的二维前缀和数组
sum,即差分数组以当前位置为右下角,原数组的左上角为左上角的区域和
s u m [ i , j ] = s u m [ i − 1 ] [ j ] + s u m [ i ] [ j − 1 ] − s u m [ i − 1 ] [ j − 1 ] + d e v [ i ] [ j ] sum[i,j] = sum[i-1][j]+sum[i][j-1]-sum[i-1][j-1]+dev[i][j] sum[i,j]=sum[i−1][j]+sum[i][j−1]−sum[i−1][j−1]+dev[i][j]-
初始时div数组需要扩展边界,转化为
sum时需要处理0class Solution { public int[][] rangeAddQueries(int n, int[][] queries) { int[][] div = new int[n + 1][n + 1]; for (int[] q : queries){ div[q[0]][q[1]]++; div[q[0]][q[3] + 1]--; div[q[2] + 1][q[1]]--; div[q[2] + 1][q[3] + 1]++; } int[][] sum = new int[n][n]; for (int i = 0; i < n; i++){ for (int j = 0; j < n; j++){ sum[i][j] = div[i][j]; if (i != 0) sum[i][j] += sum[i - 1][j]; if (j != 0) sum[i][j] += sum[i][j - 1]; if (i != 0 && j != 0) sum[i][j] -= sum[i - 1][j - 1]; } } return sum; } }- 复杂度
- 时间复杂度: O ( n 2 + q ) O(n^2+q) O(n2+q), q q q为 q u e r i e s queries queries的长度
- 空间复杂度: O ( 1 ) O(1) O(1)
- 复杂度
-
div数组边界可以+2,方便处理0
d i v [ 1 : n ] [ 1 : n ] div[1:n][1:n] div[1:n][1:n]计算为二维前缀和数组,在赋值给结果集
class Solution { public int[][] rangeAddQueries(int n, int[][] queries) { int[][] div = new int[n + 2][n + 2]; for (int[] q : queries){ div[q[0] + 1][q[1] + 1]++; div[q[0] + 1][q[3] + 2]--; div[q[2] + 2][q[1] + 1]--; div[q[2] + 2][q[3] + 2]++; } int[][] sum = new int[n][n]; for (int i = 1; i <= n; i++){ for (int j = 1; j <= n; j++){ sum[i - 1][j - 1] = (div[i][j] += div[i - 1][j] + div[i][j - 1] - div[i - 1][j - 1]); } } return sum; } }
-
-
-
进阶:子矩阵元素变化量不定
二维区域和检索 - 矩阵不可变【LC304】
Given a 2D matrix
matrix, handle multiple queries of the following type:
- Calculate the sum of the elements of
matrixinside the rectangle defined by its upper left corner(row1, col1)and lower right corner(row2, col2).Implement the
NumMatrixclass:
NumMatrix(int[][] matrix)Initializes the object with the integer matrixmatrix.int sumRegion(int row1, int col1, int row2, int col2)Returns the sum of the elements ofmatrixinside the rectangle defined by its upper left corner(row1, col1)and lower right corner(row2, col2).You must design an algorithm where
sumRegionworks onO(1)time complexity.
-
思路:在构造方法中生成矩阵
matrix的二维累加和数组,在sumRegion方法中通过累加和数组返回指定区域的和 -
实现
二维前缀和数组
sum,即以当前位置为右下角,matrix数组的左上角为左上角的区域和为了方便处理边界0,将
sum数组的周围扩展1class NumMatrix { int[][] sum; int m; int n; public NumMatrix(int[][] matrix) { m = matrix.length; n = matrix[0].length; sum = new int[m + 1][n + 1]; for (int i = 0; i < m; i++){ for (int j = 0; j < n; j++){ sum[i + 1][j + 1] = sum[i][j + 1] + sum[i + 1][j] + matrix[i][j] - sum[i][j]; } } } public int sumRegion(int row1, int col1, int row2, int col2) { return sum[row2 + 1][col2 + 1] + sum[row1][col1] - sum[row1][col2 + 1] - sum[row2 + 1][col1]; } } /** * Your NumMatrix object will be instantiated and called as such: * NumMatrix obj = new NumMatrix(matrix); * int param_1 = obj.sumRegion(row1,col1,row2,col2); */- 复杂度
- 时间复杂度:构造方法的时间复杂度为生成二维前缀和数组的时间复杂度 O ( m ∗ n ) O(m*n) O(m∗n),
sumRegion的时间复杂度为 O ( 1 ) O(1) O(1) - 空间复杂度: O ( m ∗ n ) O(m*n) O(m∗n)
- 时间复杂度:构造方法的时间复杂度为生成二维前缀和数组的时间复杂度 O ( m ∗ n ) O(m*n) O(m∗n),
- 复杂度