AcWing笔记--数字三角形模型

问题描述： 给定一个共有N行的三角矩阵A，其中第i行有j列。从左上角出发，每次可以向下方或右下方走一步，最终到达底部。求把经过的所有位置上的数加起来，和最大时多少。

原题链接：AcWing 898. 数字三角形

代码：

#include 
#include 

using namespace std;

const int N = 510;

int g[N][N],f[N][N];

int main()
{
    int n;
    cin>>n;
    for(int i = 1;i <= n;i++)
    {
        for(int j = 1;j <= i;j++)
            cin>>g[i][j];
    }
    
    for(int i = 1;i <= n;i++) f[n][i] = g[n][i];//初始化最后一行
    
    for(int i = n - 1;i >= 1;i--)//从倒数第二行开始，比较f[i+1][j]与f[i+1][j+1]的值大小
    {
        for(int j = 1;j <= i;j++)
        {
            f[i][j] = max(f[i + 1][j] + g[i][j],f[i + 1][j + 1] + g[i][j]);
        }
    }
    
    cout<<f[1][1]<<endl;//加到最后，顶点f[1][1]既是答案
    return 0;
}

-----------------------------------------------------------------------------------------

原题链接：AcWing 1015. 摘花生

分析：

代码：

#include 

using namespace std;
const int N = 110;

int w[N][N],f[N][N];

int main()
{
    int t;
    scanf("%d",&t);
    while(t--)
    {
        int r,c;
        scanf("%d%d",&r,&c);

        for(int i = 1;i <= r;i++)
        {
            for(int j = 1;j <= c;j++)
            {
                scanf("%d",&w[i][j]);
            }
        }

        for(int i = 1;i <= r;i++)
        {
            for(int j = 1;j <= c;j++)
            {
                f[i][j] = max(f[i - 1][j] + w[i][j],f[i][j - 1] + w[i][j]);
            }
        }

        cout<<f[r][c]<<endl;
    }
    return 0;
}

-----------------------------------------------------------------------------------------

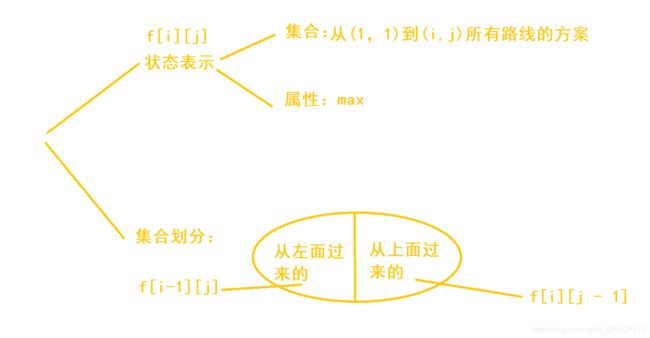
原题链接：AcWing 1018. 最低通行费

分析：
商人必须在(2N-1)个单位时间穿越出去
而正方形网格边长为N，商人初始位置在左上角
则商人只能往右或者往下走，进而转化为摘花生问题。

代码：

#include 

using namespace std;

const int N = 110;
const int INF = 1e9;
int f[N][N],w[N][N];

int main()
{
    int n;
    scanf("%d",&n);
    for(int i = 1;i <= n;i++)
    {
        for(int j = 1;j <= n;j++)
        {
            scanf("%d",&w[i][j]);
        }
    }
    
    for(int i = 1;i <= n;i++)
    {
        for(int j = 1;j <= n;j++)
        {
            if(i == 1 && j == 1) f[i][j] = w[i][j];//边界初始化为0，
            else {
                f[i][j] = INF;
                if(i > 1) f[i][j] = min(f[i][j],f[i - 1][j] + w[i][j]);// 只有不在第一行时才可以从上面过来
                if(j > 1) f[i][j] = min(f[i][j],f[i][j - 1] + w[i][j]);// 只有不在第一列时才可以从左边过来
            }
        }
    }
    
    printf("%d\n",f[n][n]);
    return 0;
}

-----------------------------------------------------------------------------------------

原题链接：AcWing 1027. 方格取数

分析：


代码：

#include 

using namespace std;

const int N = 15;

int w[N][N];
int f[N * 2][N][N];

int main()
{
    int n;
    scanf("%d",&n);
    int a,b,c;
    while(cin>>a>>b>>c,a && b && c) w[a][b] = c;
    
    for(int k = 2;k <= n + n;k++)//从（1，1）开始，k为横纵坐标之和所以起始k为i+j = 1
    {
        for(int i1 = 1;i1 <= n;i1++)
        {
            for(int i2 = 1;i2 <= n;i2++)
            {
                int j1 = k - i1,j2 = k - i2;
                if(j1 >= 1 && j1 <= n && j2 >= 1 && j2 <= n)//j1和j2要在边界内
                {
                    int t = w[i1][j1];//重合时，加任意一个就行
                    if(i1 != i2) t += w[i2][j2];//不重合时，再加上另外一个
                    int &x = f[k][i1][i2];//简化代码
                    x = max(x,f[k - 1][i1 - 1][i2 - 1] + t);//四种状态求最大值
                    x = max(x,f[k - 1][i1 - 1][i2] + t);
                    x = max(x,f[k - 1][i1][i2 - 1] + t);
                    x = max(x,f[k - 1][i1][i2] + t);
                }
            }
        }
    }
    
    cout<<f[n + n][n][n]<<endl;
    return 0;
}

-----------------------------------------------------------------------------------------

原题链接：AcWing 275. 传纸条

分析： 同方格取数

代码：

#include 

using namespace std;
const int N = 55;

int f[N * 2][N][N],w[N][N];

int main()
{
    int r,c;
    cin>>r>>c;
    for(int i = 1;i <= r;i++)
    {
        for(int j = 1;j <= c;j++)
        {
            scanf("%d",&w[i][j]);
        }
    }
    
    for(int k = 2;k <= r + c;k++)
    {
        for(int i1 = 1;i1 <= r;i1++)//i1和i2是横坐标，所以用r
        {
            for(int i2 = 1;i2 <= r;i2++)
            {
                int j1 = k - i1,j2 = k - i2;
                if(j1 >= 1 && j1 <= c && j2 >= 1 && j2 <= c)//同理用c
                {
                    int t = w[i1][j1];
                    if(i1 != i2) t += w[i2][j2];
                    int &x = f[k][i1][i2];
                    x = max(x,f[k - 1][i1 - 1][i2 - 1] + t);
                    x = max(x,f[k - 1][i1 - 1][i2] + t);
                    x = max(x,f[k - 1][i1][i2 - 1] + t);
                    x = max(x,f[k - 1][i1][i2] + t);
                }
            }
        }
    }
    printf("%d\n",f[r + c][r][r]);
    return 0;
}