初赛知识之一 —— 排序算法

标题排序算法与基础习题

马上就NOIP初赛了。
我好心（啊呸）地为大家准备了一些知识点。
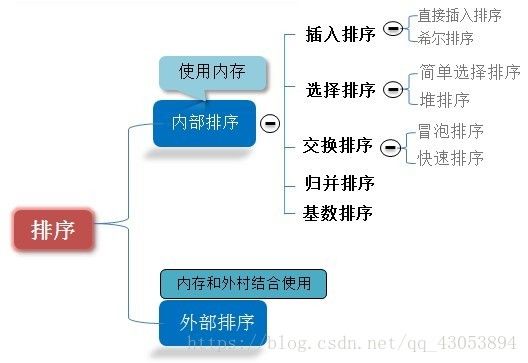
一.排序

所谓排序，就是使一串记录，按照其中的某个或某些关键字的大小，递增或递减的排列起来的操作。排序算法，就是如何使得记录按照要求排列的方法。排序算法在很多领域得到相当地重视，尤其是在大量数据的处理方面。一个优秀的算法可以节省大量的资源。在各个领域中考虑到数据的各种限制和规范，要得到一个符合实际的优秀算法，得经过大量的推理和分析。
排序(Sorting) 是计算机程序设计中的一种重要操作，它的功能是将一个数据元素(或记录)的任意序列，重新排列成一个关键字有序的序列。

稳定度(稳定性)

一个排序算法是稳定的，就是当有两个相等记录的关键字R和S，且在原本的列表中R出现在S之前，在排序过的列表中R也将会是在S之前。

当相等的元素是无法分辨的，比如像是整数，稳定度并不是一个问题。然而，假设以下的数对将要以他们的第一个数字来排序。

(4,1)(3,1)(3,7)(5,6)在这个状况下，有可能产生两种不同的结果，一个是依照相等的键值维持相对的次序，而另外一个则没有:

(3,1)(3,7)(4,1)(5,6) (维持次序)

(3,7)(3,1)(4,1)(5,6) (次序被改变)

不稳定排序算法可能会在相等的键值中改变纪录的相对次序，但是稳定排序算法从来不会如此。不稳定排序算法可以被特别地实现为稳定。作这件事情的一个方式是人工扩充键值的比较，如此在其他方面相同键值的两个对象间之比较，就会被决定使用在原先数据次序中的条目，当作一个同分决赛。然而，要记住这种次序通常牵涉到额外的空间负担。

在计算机科学所使用的排序算法通常被分类为:

(a)计算的复杂度(最差、平均、和最好性能)，依据列表(list)的大小(n)。

一般而言，好的性能是 O(nlogn)，且坏的性能是 O(n^2)。对于一个排序理想的性能是 O(n)。

而仅使用一个抽象关键比较运算的排序算法总平均上总是至少需要 O(nlogn)。

(b)存储器使用量(空间复杂度)(以及其他电脑资源的使用)

©稳定度:稳定的排序算法会依照相等的关键(换言之就是值)维持纪录的相对次序。

(d)一般的方法:插入、交换、选择、合并等等。交换排序包含冒泡排序和快速排序。插入排序包含希尔排序，选择排序包括堆排序等。
C++自带的algorithm库函数中提供了排序算法。

自带排序算法的一般形式为:

sort(arr+m,arr+n);//将数组arr的下标为m的元素到下标为n-1的元素进行从小到大排序

sort(arr+m,arr+n,comp);//与sort(arr+m,arr+n)相比，这个写法可以自己定义排序的规则，其中，comp为自定义的函数

对于sort(arr+m,arr+n)我们举个简单的例子，这个程序实现从键盘读入10个数，然后从小到大输出的功能:

当然，有时我们需要从大到小的进行排序。那么我们可以用sort(arr+m,arr+n,comp)进行排序。

不过，在调用sort(arr+m,arr+n,comp)之前我们需要自己写个comp函数。

从大到小排序的comp函数可以这样写:

下面是10个数从大到小排序的代码:

在更多情况下，我们不仅对一个特征进行排序，而是多个特征。例如将学生的成绩进行排序，当然用上面的做法是行不通的。这是，我们就想到了结构体这种数据类型。当我们采用sort()函数的默认规则排序结构体时，sort()默认结构体中的第一个成员为第一关键字，第二个成员为第二关键字，……，第N个元素为第N关键字，然后从小到大排序。

1.插入排序—直接插入排序(Straight Insertion Sort)

基本思想:

将一个记录插入到已排序好的有序表中，从而得到一个新，记录数增1的有序表。即：先将序列的第1个记录看成是一个有序的子序列，然后从第2个记录逐个进行插入，直至整个序列有序为止。

要点：设立哨兵，作为临时存储和判断数组边界之用。

直接插入排序示例：

二.冒泡排序
时间复杂度O（n 2）
通过相邻两个数的交换来去除逆序对，以达到排序的目的。
伪代码如下：

    int i <-1 i to n-1 i++
        int j <-1 j to n-i-1 j++
            if(a[i] < a[j]) a[i]<=>a[j]; 

c代码
for(int i=0; i

有一种优化的方法，设立一个中间值mid，以及j和k，j从中间向前交换，k从中间向后交换。
伪代码如下：

     int i <-1 i to n-1 i++
        int j <-(n-i-1)/2，k<- (n-i-1)/2; j to 1, k to n-i-1;  j--,k++
            if(a[i] < a[j]) a[i]<=>a[j]; 
            if(a[i] < a[k]) a[i]<=>a[k]

最后给大家推荐一段别人写的快速排序：

void quick_sort(int s[], int l, int r)
{
    if (l < r)
    {
        int i = l, j = r, x = s[l];
        while (i < j)
        {
            while(i < j && s[j] >= x) j--;// 从右向左找第一个小于x的数
            if(i < j) s[i++] = s[j];
            while(i < j && s[i] < x) i++;// 从左向右找第一个大于等于x的数
            if(i < j) s[j--] = s[i];
        }
        s[i] = x;
        quick_sort(s, l, i - 1); // 递归调用 
        quick_sort(s, i + 1, r);
    }
}

• 这一期就这样可耻的结束了。再见！