《应用统计学及R语言应用》期末考核

2019-2020学年第2学期
《应用统计学及R语言应用》课程考核材料

标题： 饭店销量预测统计建模与优化

姓名： susu
学号：
专业： big data
班级：
得分：

信息工程学院
2020年6月

---

考核说明

1.本材料作为《应用统计学及R语言应用》课程的期末考核依据，分值占期末总评成绩的50%；
2.每人完成一份，上机操作，独立完成，所有操作过程须截图，使用Ctrl+PrntScr组合键截取当前活动窗口，保持所有截图尺寸一致，且截图分辨率高，内容清晰；
3.不得抄袭，本材料除提交纸质版以外，须提供电子版，以备重复率与相似比检测。纸质版单双面打印都可；
4.排版应遵循操作步骤，整体布局美观，各级标题、字号以及版式统一。一级标题黑体四号，二级标题黑体小四，内容宋体小四，西文字体Times New Roman；
5.代码部分注意缩进，且须在重要语句位置加注释信息。
6.评分规则：
（1）（满分10分）问题分析：对问题和数据进行深入分析，理出建模的清晰思路，明确正确的统计分析方法。此项得分：
（2）（满分30分）模型构建：建立统计分析模型时要有严密的数学推理，用数学方法建模，模型要明确，要有数学表达式。此项得分：
（3）（满分30分）模型求解：设计或选择恰当地算法，利用R语言编程求解模型。此项得分：
（4）（满分20分）结果的分析和检验：对模型求解结果进行误差分析，稳定性分析等，检验模型在实际应用中的“合理可行性”。此项得分：
（5）（满分10分）模型的评价和改进：一方面对所建模型给出中肯的评价，并提出切实可行的改进意见；另一方面给出课程学习的总结。此项得分：

---

目录
1.背景与意义…1
2.问题重述 …1
3.方法简介 …2
3.1 环境 …2
3.2 方法描述 …2
3.3 时间序列…2
3.4 步骤…3
4.问题分析 …3
5.数据处理与分析 …4
5.1 一幅时间序列图 …5
5.2 对于数据季节性的分析 …6
5.3 预测第4年1~12月的各月销售量 …11
5.4 结果分析与模型评价…13
6． 总结与建议 …14

选题2：饭店销量预测统计建模与优化

1． 背景与意义
梅沙饭店坐落于一处度假胜地，该饭店由王明所有并经营，并且已经完成了第三年的经营。在这一时期，王明正试图使饭店享有专长于新鲜海味的高质量餐饮店的名声。王明和他的合作班子所做的努力，经证明是成功的，他的饭店已经成为度假胜地最好并且增长最快的饭店之一。王明认为要想为饭店未来的增长计划得更好，他必须开发一套系统。该系统应可以使他提前一年预测出月度食品和饮料销售额。
应用统计学与概率论等相关知识，对所给案例进行分析预测。对梅沙饭店对销售数据进行分析。准备一篇报告以总结发现、预测以及建议。

2． 问题重述
王明认为要想为饭店未来的增长计划得更好，他必须开发一套系统。该系统应可以使他提前一年预测出月度食品和饮料销售额。王明拥有过去3年食品和饮料总体销售情况的数据：

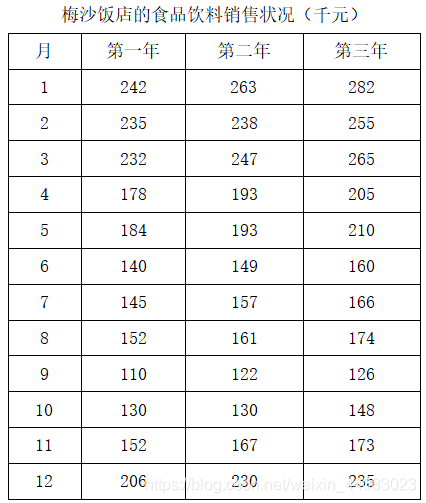
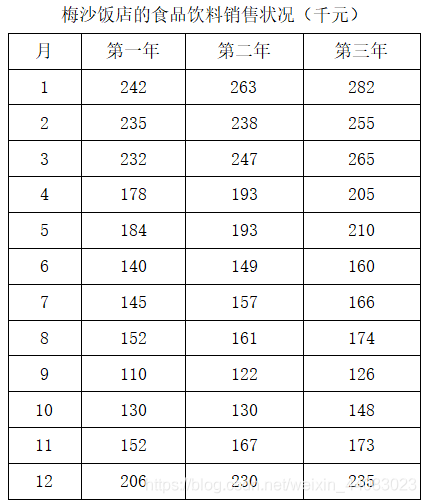
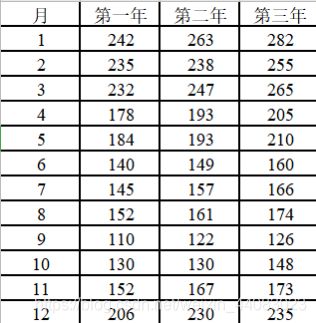
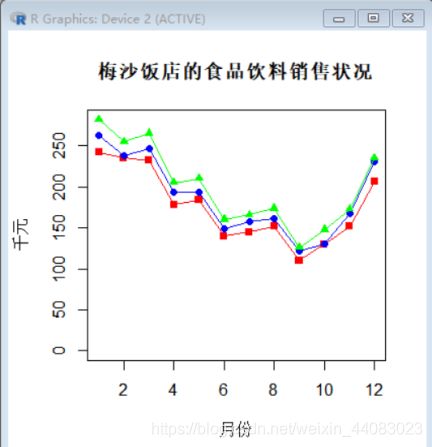
梅沙饭店的食品饮料销售状况（千元）
月 第一年 第二年 第三年
1 242 263 282
2 235 238 255
3 232 247 265
4 178 193 205
5 184 193 210
6 140 149 160
7 145 157 166
8 152 161 174
9 110 122 126
10 130 130 148
11 152 167 173
12 206 230 235
为梅沙饭店对销售数据进行分析。为王明准备一篇报告以总结你的发现、预测以及建议。
需包括如下内容：
（1）一幅时间序列图。
（2）对于数据季节性的分析。指出每个月的季节指数，并说说高销售量月份以及低销售量月份的情况，从直觉而言，使用季节指数有意义吗？试讨论。
（3）预测第4年1~12月的各月销售量。
（4）假设第4年1月的销售额为295000元。你的预测误差为多少？如果这一误差很大，王明或许会因为你的预测值与实际销售值之间的差距而困惑。你可以做出什么来消除他的困惑及他对预测过程的怀疑。

3． 方法简介
针对实际问题， 我们需要通过对历史数据的分析， 运用统计学方法确定年月份对应饮料销量的关系，将原来的销售分解为四部分来看——趋势、周期、时期和不稳定因素， 然后综合这些因素，提出销售预测。强调的是通过对一个区域进行一定时间段内的连续遥感观测，提取图像有关特征，并分析其变化过程与发展规模。当然，首先需要根据检测对象的时相变化特点来确定遥感监测的周期，从而选择合适的遥感数据。
给出准则： 当给定新月份下每一样本对应的各项销售指标时， 能准确的判断其对应的销量。
3.1环境
R语言编译器
3.2方法描述
利用R语言将所给数据编译为折线图，并对案例进行分析预测建立统计分析模型时要有严密的数学推理，用数学方法建模，模型要明确，要有数学表达式。对问题和数据进行深入分析，理出建模的清晰思路，明确正确的统计分析方法。设计或选择恰当地算法，利用R语言编程求解模型；对模型求解结果进行误差分析，稳定性分析等，检验模型在实际应用中的“合理可行性”。一方面对所建模型给出中肯的评价，并提出切实可行的改进意见；另一方面给出课程学习的总结。
3.3时间序列
按照时间的顺序将随机事件变化发展的过程记录下来的数据就构成时间序列，对于时间序列进行观察研究，找寻它的变化和发展规律，预测它将来的趋势。
时间序列是按时间顺序的一组数字序列
时间序列的特点：现实的、真实的一组数据，而不是数理统计中做实验得到的。既然是真实的，它就是反映某一现象的统计指标，因而，时间序列背后是某一现象的变化规律。动态数据。
3.4步骤
基本步骤是：
（1）用观测、调查、统计、抽样等方法取得被观测系统时间序列动态数据。
（2）根据动态数据作相关图，进行相关分析，求自相关函数。相关图能显示出变化的趋势和周期，并能发现跳点和拐点。跳点是指与其他数据不一致的观测值。如果跳点是正确的观测值,在建模时应考虑进去，如果是反常现象，则应把跳点调整到期望值。拐点则是指时间序列从上升趋势突然变为下降趋势的点。如果存在拐点，则在建模时必须用不同的模型去分段拟合该时间序列，例如采用门限回归模型。
（3）辨识合适的随机模型，进行曲线拟合，即用通用随机模型去拟合时间序列的观测数据。对于短的或简单的时间序列，可用趋势模型和季节模型加上误差来进行拟合。对于平稳时间序列，可用通用ARMA模型（自回归滑动平均模型）及其特殊情况的自回归模型、滑动平均模型或组合-ARMA模型等来进行拟合。当观测值多于50个时一般都采用ARMA模型。对于非平稳时间序列则要先将观测到的时间序列进行差分运算，化为平稳时间序列，再用适当模型去拟合这个差分序列。

4.问题分析
确定性时序分析的目的：克服其它因素的影响，单纯测度出某一个确定性因素对序列的影响；推断出各种确定性因素彼此之间的相互作用关系及它们对序列的综合影响。时间序列趋势分析目的：有些时间序列具有非常显著的趋势，我们分析的目的就是要找到序列中的这种趋势，并利用这种趋势对序列的发展作出合理的预测。
可以看出该问题适合使用：
一般用ARMA模型拟合时间序列，预测该时间序列未来值。
（1）趋势拟合法：就是把时间作为自变量，相应的序列观察值作为因变量，建立序列值随时间变化的回归模型的方法。包括线性拟合和非线性拟合。线性拟合的使用场合为长期趋势呈现出线形特征的场合。参数估计方法为最小二乘估计。
（2）指数平滑法：进行趋势分析和预测时常用的一种方法。它是利用修匀技术，削弱短期随机波动对序列的影响，使序列平滑化，从而显示出长期趋势变化的规律。Holt-Winters指数平滑法(增长或降低趋势、季节性变化、相加模型的时间序列)
（3）平均数法：把若干历史时期的统计数值作为观察值，求出算术平均数作为下期预测值。这里用加权平均数法：把各个时期的历史数据按近期和远期影响程度进行加权，求出平均值，作为下期预测值。
（4）趋势推测法：当时间序列中包含有趋势成分是可以采用回归分析的方法对趋势做推测。如果样本数据对时间做表绘图显现某种线性趋势时，则可以假定时间序列中长期成分用简单线性回归。

5.数据处理与分析
数据：

5.1 一幅时间序列图
（1）利用题目创建数据xlsl表格

（2）转换为.csv格式读取数据

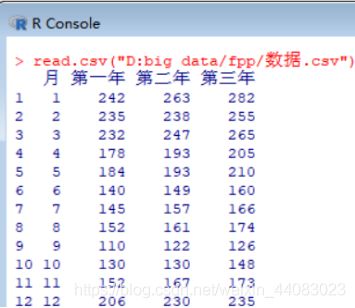
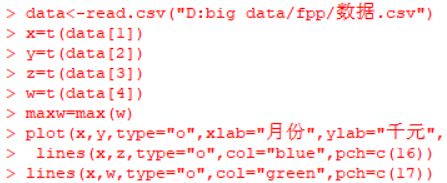
（3）读取数据用plot函数生成折线图
实现代码：

> data<-read.csv("D:big data/fpp/数据.csv")
> x=t(data[1])
> y=t(data[2])
> z=t(data[3])
> w=t(data[4])
> maxw=max(w)
> plot(x,y,type="o",xlab="月份",ylab="千元",ylim=c(0,maxw),col="red",main="梅沙饭店的食品饮料销售状况",pch=c(15))
>  lines(x,z,type="o",col="blue",pch=c(16))
> lines(x,w,type="o",col="green",pch=c(17))

5.2对于数据季节性的分析
指出每个月的季节指数，并说说高销售量月份以及低销售量月份的情况，从直觉而言，使用季节指数有意义吗？试讨论。
（1）整理数据写到纯文本文件中

（2）假设第一年为2017年，生成时间序列
x <- scan(“D:/big data/fpp/chap10/月份.txt”); xtimeseries
<- ts(x,frequency=12, start = c(2017,1))
Read 36 items
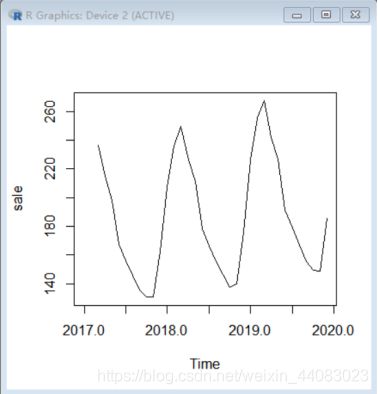
plot.ts(xtimeseries)
abline(lm(xtimeseries~time(xtimeseries))) #增加拟合性

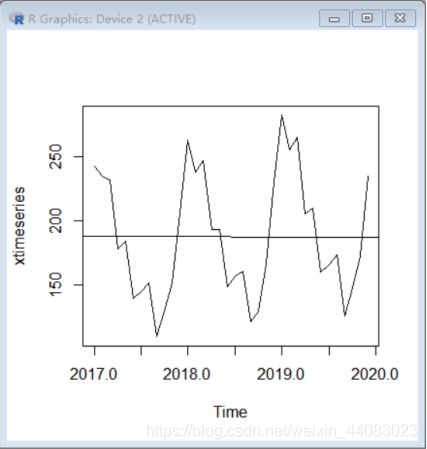
（3）时间序列分解生成季节变动图
在R的“TTR”包中的SMA()函数可以用简单的移动平均来平滑时间序列数据
#使用SMA()函数时，你需要通过参数“n”指定来简单移动平均的跨度

安装library(TTR)

> library(TTR)
> sale<-SMA(xtimeseries,n=3)
> plot.ts(sale)

（4）分解季节性数据(季节部分+趋势部分+不规则部分) #对于可以使用相加模型进行描述的时间序列中的趋势部分和季节性部分，我们可以使用R中“decompose()”函数来估计。这个函数可以估计出时间序列中趋势的、季节性的和不规则的部分。

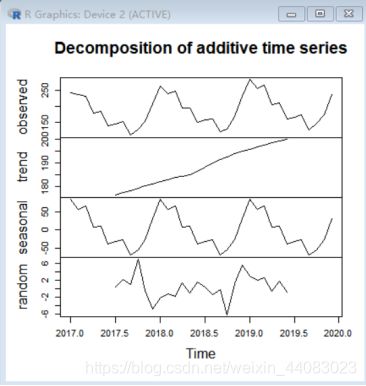
salecomponents<-decompose(xtimeseries)
plot(slecomponents)
#从原时间序列中去除去季节部分。
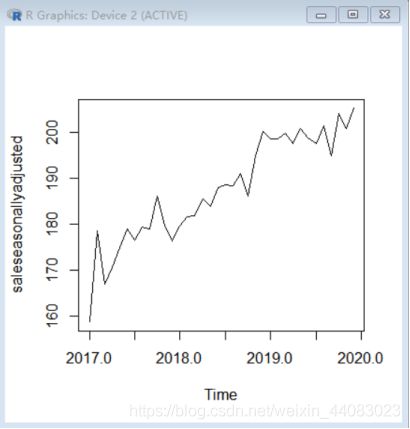
saleseasonallyadjusted<-xtimeseries-salecomponents$seasonal
#我们可以使用“plot()”画出季节性修正时间序列，代码如下：
plot(saleseasonallyadjusted)

季节性修正时间序列

（5）计算中心化移动平均值CMA。
moving <- function(x, k = 1, weighted = FALSE){
n <- length(x); f <- numeric(0)
if (weighted == TRUE | weighted == T){
w <- k:1
} else{
w <- rep(1, k)
}
for (t in k:n){
f[t+1] <- weighted.mean(x[t:(t-k+1)], w)
}
mse <- sum((x[(k+1):n]-f[(k+1):n])^2)/(n-k)
list(average = f, MSE = mse)
}

（6）整理每个月份季度指数
制作成纯文本文件

（7）绘制折线图
x=t(data[1])
y=t(data[2])
plot(x,y,type=“o”,xlab=“月份”,ylab=“指数”,ylim=c(0,2),col=“red”,main=“季节指数”,pch=c(15))

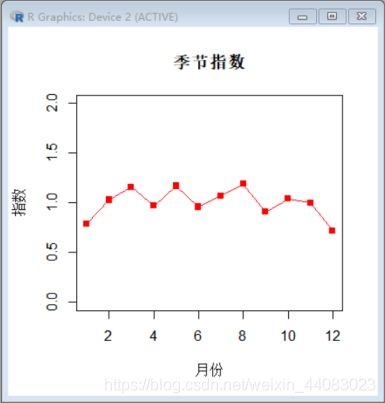
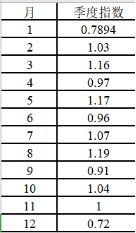
从上图中可以得出销售的旺季是三月、五月、八月，其中销售最旺的季节是八月
份，该月的销售额相当于全年月平均销售额的119%;销售量最低的月份是十二月
份，该月的销售额相当于全年月平均销售额的72%。从直觉上看，适用季节指数
有意义，因为计算出季节指数，可以用来预测未来的各月份的销售情况,还可以
用来从原时间序列中分离出季节变动，以便更清晰地显示其他成分的变化形态。

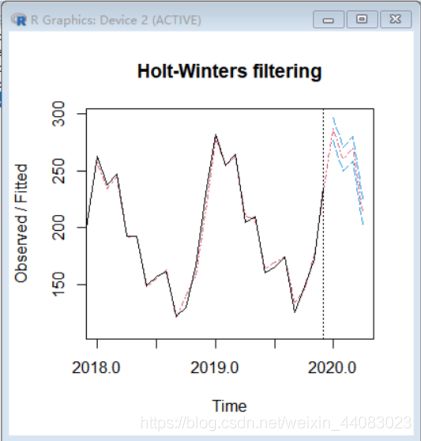
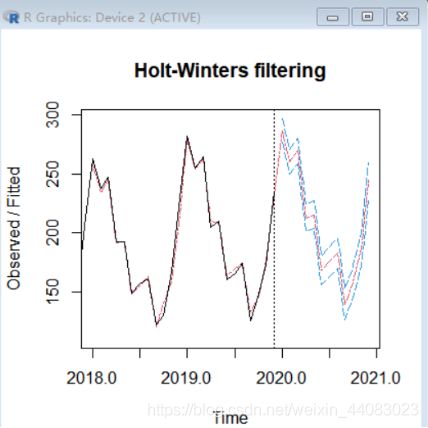
5.3 预测第4年1~12月的各月销售量
我决定使用Holt- Winters指数平滑方法进行预测

x <- scan(“D:/big data/fpp/chap10/月份.data”)
Read 36 items
#生成12月季节时间序列，假设开始时间为2017年，预测2020年销售情况

x <- ts(x, start=2017, frequency = 12)
#完成指数平滑
m <- HoltWinters(x)
#生成预测值
p <- predict(m, n.ahead = 4, prediction.interval = TRUE)

#生成图像

plot(m, p, lty.predicted = 4, lty.intervals = 5)
4个月

#生成一年预测值

p <- predict(m, n.ahead = 12, prediction.interval = TRUE)

#生成图像

plot(m, p, lty.predicted = 12, lty.intervals = 5)

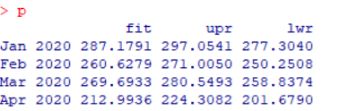
数据值：
Jan 2020 287.1791 297.0541 277.3040
Feb 2020 260.6279 271.0050 250.2508
Mar 2020 269.6933 280.5493 258.8374
Apr 2020 212.9936 224.3082 201.6790
May 2020 215.6079 227.3632 203.8525
Jun 2020 168.6415 180.8216 156.4615
Jul 2020 175.9412 188.5318 163.3507
Aug 2020 182.9764 195.9645 169.9884
Sep 2020 139.4964 152.8702 126.1227
Oct 2020 158.1483 171.8969 144.3996
Nov 2020 185.4633 199.5769 171.3497
Dec 2020 244.6490 259.1183 230.1797

5.4 预测误差判断
如果这一误差很大，王明或许会因为你的预测值与实际销售值之间的差距而困惑。你可以做出什么来消除他的困惑及他对预测过程的怀疑。
通过上题给出的数据可以看到一月的：
预测值约为287179元 误差：-7.8209千
预测上限为297054元 误差：2.0541 千
预测下限为277304元 误差：17.696 千
与预测值相差不是太大，但是也有近千元，数据在可预测范围内可见模型还是可取的，毕竟销售是认为的，其中可能因为环境，销售方法，销售的人等等各种因素影响销售值，所以用公式计算不可能完全符合。
但是如果没有大的影响，这个模型还是可取的，我根据所给的数据生成时间序列，发现销量是有一个增长或降低趋势并存在季节性可被描述成为相加模型的时间序列的，这基本符合我选的霍尔特-温特指数平滑法对其进行短期预测。

6． 总结与建议
回顾这次课程设计，感触很深，收获颇丰。经过动手我更加认识到实践是检验真理的唯一标准，只学不实践，那么所学的就等于零，理论应当与实践相结合。另一方面，实践可为以后找工作打基础。我感觉实践是大学生活的第二课堂，是知识常新和发展的源泉，是检验真理的试金石，也是大学生锻炼成长的有效途径。一个人的知识和本事仅有在实践中才能发挥作用，才能得到丰富、完善和发展。大学生成长，就要勤于实践，将所学的理论知识与实践相结合一齐，在实践中继续学习，不断总结，逐步完善，有所创新，并在实践中提高自我的各方面知识、本事、技术等因素融合成的综合素质和本事，为自我事业的成功打下良好的基础。
　　经过这次课程设计，学到一些在学校里学不到的东西。在这两天里，我深入课本案例，认真学习、努力工作，本事有了很大的提高，个人综合素质也有了全面的发展，但我明白还存在着一些缺点和不足。认识到经验的缺乏，所以我必须进取努力。在实习的这段时间里，虽然有时候很难，可是感到更加的充实，我从中体会到了做人做事的道理，从实践中学到了专业技术，积累了实践技术经验。在今后的工作和学习中，我还要更进一步严格要求自我，虚心向优秀的人学习，继续努力改正自我的缺点和不足，争取在思想、工作、学习和生活等方面取得更大的提高。