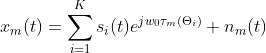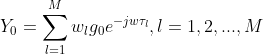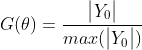《阵列信号处理及MATLAB实现》信源和噪声模型、阵列天线统计模型
PS:文章内容为本人读书笔记,如想阅读更详细内容请购买正版书籍
2.5 信源和噪声模型
2.5.1 窄带信号
如果信号带宽远小于其中心频率,则该信号为窄带信号,即:
![]()
其中,![]() 为信号带宽,
为信号带宽,![]() 为中心频率。通常将正弦信号和余弦信号统称为正弦型信号,正弦型信号是典型的窄带信号。若无特殊说明,本书中所提及的窄带信号表示为:
为中心频率。通常将正弦信号和余弦信号统称为正弦型信号,正弦型信号是典型的窄带信号。若无特殊说明,本书中所提及的窄带信号表示为:
![]()
式中,![]() 为慢变幅度调制函数(或称实包络),
为慢变幅度调制函数(或称实包络),![]() 为慢变相位调制函数,
为慢变相位调制函数,![]() 为载频。一般情况下,
为载频。一般情况下,![]() 和
和![]() 包含了全部有用信息。
包含了全部有用信息。
2.5.2 相关系数
对于接受到的多个信号,一般可利用相关系数(或称互相关系数)来衡量信号之间的关联程度。对于两个平稳信号![]() 和
和![]() ,其相关系数定义为:
,其相关系数定义为:
当![]() 时,称
时,称![]() 和
和![]() 不相关(或称不相干);当
不相关(或称不相干);当![]() 时,称
时,称![]() 和
和![]() 部分相关;当
部分相关;当![]() 时,称
时,称![]() 和
和![]() 完全相关(或称相干)
完全相关(或称相干)
2.5.3 噪声模型
本书中,无特殊说明,阵元接收到的噪声均假设为平稳零均值高斯白噪声,方差为![]() 。各阵元间噪声互不相关,且与目标源不相关。这样,噪声向量
。各阵元间噪声互不相关,且与目标源不相关。这样,噪声向量![]() 的二阶矩满足:
的二阶矩满足:
![]()
![]()
2.6 阵列天线的统计模型
2.6.1 前提及假设
关于接收天线阵的假设:接收阵列由位于空间已知坐标处的无源阵元按一定的形式排列而成。假设阵元的接收特性仅与位置有关而与尺寸无关(认为是一个点),并且阵元都是全向阵元,增益均相等,相互之间互耦忽略不计。阵元接收信号时将产生噪声,假设其为加性高斯白噪声,各阵元上的噪声相互统计独立,且噪声与信号是统计独立的。
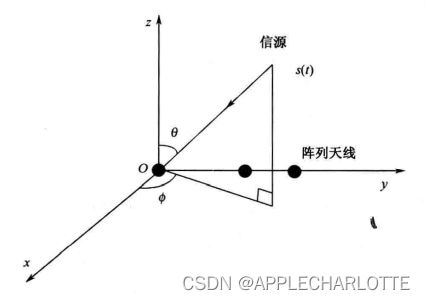
关于空间源信号的假设:假设空间信号的传播介质是均匀且各向同性的,这是空间信号在介质中按直线传播;同时假设阵列处于空间信号辐射的远场中,所以空间源信号到达阵列时可以看做平行平面波,则空间源信号到达阵列各阵元在时间上的不同时延,可由阵列的几何结构和空间波来向决定。空间波的来向在三维空间中常用仰角和方位角来表征。
2.6.2 阵列的基本概念
令信号载波为![]() ,并以平面波形式在空间沿波数向量
,并以平面波形式在空间沿波数向量![]() 的方向传播,设基准点处的信号为
的方向传播,设基准点处的信号为![]() ,则距离基准点r处的阵元接收信号为:
,则距离基准点r处的阵元接收信号为:
式中,![]() 为波数向量;
为波数向量;![]() 为电磁波传播方向单位向量;
为电磁波传播方向单位向量;![]() 为波数,其中c为光速,
为波数,其中c为光速,![]() 为电磁波的波长;
为电磁波的波长;![]() 为信号相对于基准点的延迟时间;
为信号相对于基准点的延迟时间;![]() 为电磁波传播到离基准点r处的阵元相对于电磁波传播到基准点的滞后相位。
为电磁波传播到离基准点r处的阵元相对于电磁波传播到基准点的滞后相位。![]() 为电磁波传播方向角,他是相对于x轴的逆时针旋转方向定义的,显然,波数向量可表示为:
为电磁波传播方向角,他是相对于x轴的逆时针旋转方向定义的,显然,波数向量可表示为:
![]()
电磁波从点辐射源以球面波向外传播,只要距离足够远,在接收的局部区域,球面波可以近似为平面波。
设在空间有M个阵元组成阵列,阵元从1到M编号,并以阵元1(也可以选择其他阵元)作为基准或参考点。设各阵元无方向性(全向),相对于基准点的位置向量分别为![]() 。若基准点接收信号为
。若基准点接收信号为![]() ,则各阵元上的接收信号分别为:
,则各阵元上的接收信号分别为:
在通信中,信号的频带B比载波值w小得多,所以s(t)的变化相对缓慢,延时![]() ,故有:
,故有:![]() ,即信号包络在各阵元上的差异可忽略,称为窄带信号。
,即信号包络在各阵元上的差异可忽略,称为窄带信号。
此外,阵列信号总是变换到基带再进行处理,因而可将阵列信号用向量形式表示为:
![]()
上式中的向量部分称为方向向量,因为当波长和阵列的几何结构确定时,该向量只与到达波的空间角向量![]() 有关,方向向量记作
有关,方向向量记作![]() 。例如,若选择第一个阵元为基准点,则方向向量为:
。例如,若选择第一个阵元为基准点,则方向向量为:
![]()
公式中:![]()
实际使用的阵列结构要求方向向量![]() 必须与空间角向量
必须与空间角向量![]() 一一对应,不能出现模糊现象。当有多个(例如K个)信源时,到达波的方向向量可分别用
一一对应,不能出现模糊现象。当有多个(例如K个)信源时,到达波的方向向量可分别用![]() 表示。这K个方向向量组成的矩阵
表示。这K个方向向量组成的矩阵![]() 称为阵列的方向矩阵或响应矩阵,它表示所有信号源的方向。
称为阵列的方向矩阵或响应矩阵,它表示所有信号源的方向。
改变空间角![]() ,使方向向量
,使方向向量![]() 在M维空间内扫描,所形成的曲面称为阵列流行。
在M维空间内扫描,所形成的曲面称为阵列流行。
阵列流行常用符号A表示,即有:
![]()
其中,![]() 是波达方向
是波达方向![]() 所有可能取值的集合。因此阵列流行A是阵列方向向量的集合。阵列流行A包含了阵列几何结构、阵元模式、阵元间的耦合、频率等影响。
所有可能取值的集合。因此阵列流行A是阵列方向向量的集合。阵列流行A包含了阵列几何结构、阵元模式、阵元间的耦合、频率等影响。
2.6.3 天线阵模型
假设有一个天线阵列,由M具有任意方向性的阵元按任意排列构成。同时设有K个具有相同中心频率![]() 、波长
、波长![]() 的空间窄带平面波(M>K)分别以来向角
的空间窄带平面波(M>K)分别以来向角![]() 入射到该阵列。如下图所示。
入射到该阵列。如下图所示。
其中![]() 。
。![]() 和
和![]() 分别是第i个入射信号的仰角和方位角,
分别是第i个入射信号的仰角和方位角,![]()
则阵列第m个阵元的输出可以表示为:
其中,![]() 为入射到阵列的第i个源信号,
为入射到阵列的第i个源信号,![]() 为第m个阵元的加性噪声,
为第m个阵元的加性噪声,![]() 为来自
为来自![]() 方向的源信号投射到第m个阵元时,相对于选定参考点的时延。并记:
方向的源信号投射到第m个阵元时,相对于选定参考点的时延。并记:
![]()
![]()
另外,S(t)为Kx1维列向量
![]()
![]() 为MxK矩阵的方向矩阵:
为MxK矩阵的方向矩阵:![]()
矩阵![]() 中任一列向量
中任一列向量![]() 是阵列在空间源信号中一个来向为
是阵列在空间源信号中一个来向为![]() 的方向向量,且是Mx1维列向量:
的方向向量,且是Mx1维列向量:![]()
因此,如果用矩阵描述,即使在最一般化的情况下,阵列信号模型可简单的表示为:
![]()
很显然,方向矩阵![]() 与矩阵的形状、信号源的来向有关,而一般在实际应用中,天线阵的形状一旦固定就不会再改变。所以,矩阵
与矩阵的形状、信号源的来向有关,而一般在实际应用中,天线阵的形状一旦固定就不会再改变。所以,矩阵![]() 中任意一列总是和某个空间源信号的来向是紧密联系着的。
中任意一列总是和某个空间源信号的来向是紧密联系着的。
2.6.4 阵列的方向图
阵列输出的绝对值与来波方向之间的关系称为天线的方向图。方向图一般有两类,一类是阵列输出 的直接相加(不考虑信号及其来向),即静态方向图;另一类是带指向的方向图(考虑信号指向),当然信号的指向是通过控制加权的相位来实现的。从前面的信号模型可知,对于某一确定的![]() 元空间阵列,在忽略噪声的条件下,第
元空间阵列,在忽略噪声的条件下,第![]() 个阵元的复振幅为:
个阵元的复振幅为:
![]()
式中,![]() 为来波的复振幅,
为来波的复振幅,![]() 为第
为第![]() 个阵元与参考点之间的延迟。设第
个阵元与参考点之间的延迟。设第![]() 个阵元的权值为
个阵元的权值为![]() ,那么所有阵元加权的输出结果为:
,那么所有阵元加权的输出结果为:
对上式取绝对值并归一化之后可得到空间阵列的方向图![]() 为:
为:
如果式中![]() 上式则成为静态方向图
上式则成为静态方向图![]()
下面考虑均匀线列阵的方向图。假设均匀线列阵的间距为![]() ,且以最左边的阵元为参考点;另假设信号入射方位角为
,且以最左边的阵元为参考点;另假设信号入射方位角为![]() ,其中方位角表示信号入射方向与线阵法线方向的夹角。则第
,其中方位角表示信号入射方向与线阵法线方向的夹角。则第![]() 个阵元与参考点的波程差(时延)为
个阵元与参考点的波程差(时延)为![]() ,则阵列的输出为:
,则阵列的输出为:
上式中,![]() ,
,![]() ,
,![]() 为入射信号的波长。
为入射信号的波长。
当上式中![]() 时,公式可以进一步化简为:
时,公式可以进一步化简为:
可得均匀线阵的静态方向图为(公式2.6.17):
当上式中![]() 时,公式可以简化为:
时,公式可以简化为:
![]()
于是可得指向为![]() 的阵列方向图为(公式2.6.19):
的阵列方向图为(公式2.6.19):
![]()
2.6.5 波束宽度
线阵的测向范围为[-90°,90°],而一般的面阵(如圆阵)的测向范围为[-180°,180°]。为了说明波束宽度,下面只考虑线阵。
由公式2.6.17可知,M个阵元的均匀线阵的静态方向图为:
式中,空间频率![]()
这对于天线静态方向图主瓣的零点,由![]() 可得零点波束宽度
可得零点波束宽度![]() 为:
为:
![]()
而由![]() 可得到半功率点波束宽度
可得到半功率点波束宽度![]() ,在
,在![]() 的条件下有:
的条件下有:
![]()
本书中一般考虑的是静态方向图的半功率点波束宽度,即对于均匀线阵而言,其波束宽度为:
式中,D为天线的有效孔径,![]() 为信号的波长,rad表示弧度单位。对于M阵元的等距均匀线阵,阵元间距为
为信号的波长,rad表示弧度单位。对于M阵元的等距均匀线阵,阵元间距为![]() ,则天线的有效孔径为
,则天线的有效孔径为![]() ,所以对于ULA阵,阵列波束宽度的近似计算公式为:
,所以对于ULA阵,阵列波束宽度的近似计算公式为:
![]()
关于波束宽度,以下几点需要注意。
(1)波束宽度与天线孔径成反比,一般情况下天线的半功率点波束宽度与天线孔径之间关系为:
(2)对于某些阵列(如线阵),天线的波束宽度与波束指向有关系,如波束指向为![]() 时,均匀线阵的波束宽度为:
时,均匀线阵的波束宽度为:
![]()
(3)波束宽度越窄,阵列的指向性越好,也就说明阵列分辨空间信号的能力越强。
2.6.6 分辨率
阵列测向中,在某方向上对信源的分辨率与在该方向附近阵列方向矢量的变化率直接相关。在方向矢量变化较快的方向附近,随信源角度变化阵列快拍数据变化也越大,相应的分辨率也高。定义一个表征分辨率![]()
![]() 越大表示在该方向的分辨率越高。
越大表示在该方向的分辨率越高。
对于均匀线阵,有![]() ,说明信号在0°方向分辨率最高,而在60°方向分辨率已经降了一半,所以一般线阵的测向范围为-60°到60°。
,说明信号在0°方向分辨率最高,而在60°方向分辨率已经降了一半,所以一般线阵的测向范围为-60°到60°。