使用OLS摘要解释线性回归的结果
下面是一个回归过程,用于拟合收入和教育情况
import pandas as pd
import matplotlib.pyplot as plt
import seaborn as sms
import statsmodels.api as sn
sdata = pd.read_csv('../input/traindatas/char7/Salary_Data.csv')
print(sdata.head())
n = sdata.shape[0]
x_sum = sdata.YearsExperience.sum()
y_sum = sdata.Salary.sum()
x_sum2 = sdata.YearsExperience.pow(2).sum()
x_y = sdata.YearsExperience * sdata.Salary
xy = x_y.sum()
b = (xy-(x_sum * y_sum)/n)/(x_sum2 -x_sum**2/n)
print("b= ",b,sep=" ")
sms.lmplot(x= 'YearsExperience',y = "Salary",data=sdata)
plt.show()
fit = sn.formula.ols("Salary~YearsExperience",data= sdata).fit()
print(fit.summary())
输出结果如下
OLS Regression Results
==============================================================================
Dep. Variable: Salary R-squared: 0.957
Model: OLS Adj. R-squared: 0.955
Method: Least Squares F-statistic: 622.5
Date: Sun, 02 May 2021 Prob (F-statistic): 1.14e-20
Time: 11:06:19 Log-Likelihood: -301.44
No. Observations: 30 AIC: 606.9
Df Residuals: 28 BIC: 609.7
Df Model: 1
Covariance Type: nonrobust
===================================================================================
coef std err t P>|t| [0.025 0.975]
-----------------------------------------------------------------------------------
Intercept 2.579e+04 2273.053 11.347 0.000 2.11e+04 3.04e+04
YearsExperience 9449.9623 378.755 24.950 0.000 8674.119 1.02e+04
==============================================================================
Omnibus: 2.140 Durbin-Watson: 1.648
Prob(Omnibus): 0.343 Jarque-Bera (JB): 1.569
Skew: 0.363 Prob(JB): 0.456
Kurtosis: 2.147 Cond. No. 13.2
==============================================================================
Notes:
[1] Standard Errors assume that the covariance matrix of the errors is correctly specified.
第一部分
1、Dep. Variable:
因变量是一个将依赖于其他变量的变量。在此回归分析中,Y是我们的因变量,因为我们想分析X对Y的影响
2、 Model:
所述的方法普通最小二乘法(OLS)是最广泛使用的模型由于其效率。该模型给出了真实人口回归线的最佳近似值。
3、 No. Observations:
观察次数是我们样本的大小,
4、Df Residuals:
残差的自由度(Df),Df = N – K (N =样本数量(观察数), K =变量数+ 1)
5、 Df Model:
模型的Df = K – 1 = 2 – 1 = 1 (其中,K =变量数+ 1)
第二部分
1、Intercept :
常数项是回归线的截距。从回归线(eq…1)处,截距为2.579e+04。在回归中,我们忽略了一些对因变量没有太大影响的自变量,截距表明了这些遗漏变量的平均值和模型中存在的噪声。
2、coef(Coefficient term):
系数项表示X 单位变化时Y的变化,即,如果X上升1个单位,则Y上升9449.9623 。如果您熟悉导数,则可以将其视为Y相对于X的变化率。
3、 std err:
标准误差也称为标准偏差。标准误差显示这些参数的采样变异性。标准误差的计算公式为
截距项的标准误

系数项的标准误差:

σ 2 σ^2 σ2是回归(SER)的标准误差
4、t
t –统计数据: 从理论上讲,我们假设误差项服从正态分布,因此参数b 1 和 b 2 也具有正态分布,并且在上面计算出了标准误差。
b 1 ∼ N ( B 1 , σ b 1 2 ) b 2 ∼ N ( B 2 , σ b 2 2 ) B 1 和 B 2 在 这 里 是 b 1 和 b 2 的 均 值 。 b1 ∼ N(B_1, σ_{b1}^2) \\ b2 ∼ N(B_2 , σ_{b2}^2) \\ B_1和B_2 在这里是b1和b2的均值。 b1∼N(B1,σb12)b2∼N(B2,σb22)B1和B2在这里是b1和b2的均值。
t –假设以下假设来计算统计量–
H 0 : B 2 = 0 ( 变 量 X 对 Y 无 影 响 ) H a : B 2 ≠ 0 ( X 对 Y 的 影 响 很 大 ) H_0 :B_2 = 0(变量X对Y无影响)\\ H_a :B_2 ≠0(X对Y的影响很大) H0:B2=0(变量X对Y无影响)Ha:B2=0(X对Y的影响很大)
5、P>|t|
当原假设成立拒绝原假设的概率
6、[0.025 0.975]
这个是置信区间,表示95%的可能结果落的范围
第三部分

1、 R-squared:
R –平方值: R 2 R^2 R2是确定系数,它告诉我们自变量可以解释多少百分比的自变量。

Adj. R-squared:
如果在现有模型中,再加入一个“无关自变量”,则R-squared的值仍然会增加,但是,实质上,模型的拟合度并未增加;为了弥补R-squared的缺陷,提出了Adj. R-squared,它在R-squared的基础上,加入了一个“惩罚项”,当向现有模型加入一个“无关自变量”时,Adj. R-squared会给这个“无关自变量”一个惩罚,从而使得Adj. R-squared的值不一定增加,防止了“虚假提升信息的产生”
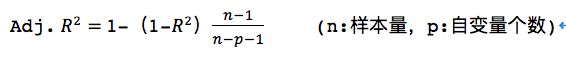
3、F-statistic:
用于完成模型的显著性检验,模型的显著性检验是指构成因变量的线性组合是否有效,具体检验步骤如下:
1)提出问题的原假设和备择假设:
原假设:模型的所有偏回归系数为零。
备择假设:模型的所有偏回归系数不全为零,即至少存在一个自变量可以构成因变量的线性组合。
由于TSS=ESS+RSS, TSS不会随着模型的变化而变动,所以,ESS和RSS之间存在的严格的负相关关系。如果ESS达到最小,RSS则会最大,进而RSS与ESS的商也会达到最大,由此构造F-statistic。公式如下:
F = E S S / k R S S / ( n − k − 1 ) F= \frac {ESS/k}{RSS/(n-k-1)} F=RSS/(n−k−1)ESS/k
模型拟合得越好,F-statistic越大。
4、AIC:
赤池信息准则,含义为用最少的自变量达到最好的拟合效果

