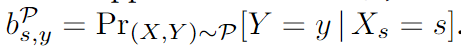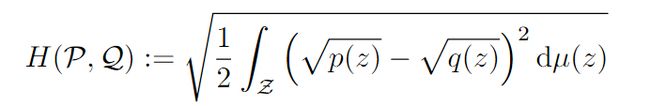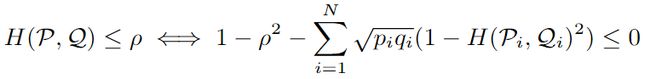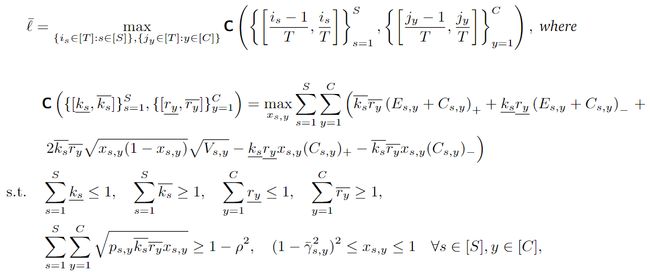Certifying Some Distributional Fairness with Subpopulation Decomposition
文章目录
- Certifying Some Distributional Fairness with Subpopulation Decomposition
- 1. 介绍
- 2. 基于公平约束分布的可验证公平性
-
- 2.1 可验证公平性
- 3. 公平性认证框架
-
- 3.1 子群分解【核心】
- 3.2 具有敏感偏移的可验证公平性
- 3.3 具有一般偏移的可验证公平性
- 附录
-
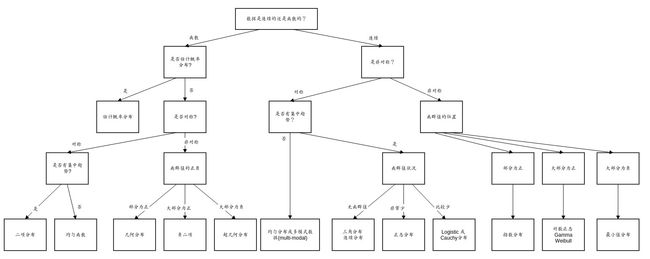
- 数据分布
Certifying Some Distributional Fairness with Subpopulation Decomposition
使用子群分解验证一些分布公平性
背景:基于不同公平衡量标准,广泛的努力被用来理解和提高机器学习模型公平性,尤其是在高风险领域,例如医疗保险、教育、招聘决定等。
问题与缺陷:端到端的机器学习模型的性能缺乏可验证公平性。
方法与模型:
在给定数据分布上,训练后的 ML 模型的验证公平性表述为 基于公平约束分布上的模型性能损失界限的优化问题,该公平约束分布在训练数据分布的有界分布距离内。
贡献:
- 提出一个通用的公平性验证框架,并用敏感偏移与一般偏移进行实例化验证。
- 将源数据分布分解为可分析性的子群分布,通过证明子问题的凸性来解决子问题,从而解决模型优化问题。
- 实验证明:模型的可验证性在敏感偏移的场景下是严格的,在一般偏移下是非平凡的。
- 框架能灵活整合额外的非偏约束,同时结果将更加严格。
- 所提的可验证公平性界限与高斯分布上的现有自适应分布鲁棒性界限进行比较,结果表明前者更加严格。
1. 介绍
先前工作存在的缺陷:
-
先前的工作主要是正则化训练、解纠缠、对偶、低阶矩阵分解、分布对齐等方法,来提高ML的公平性。
-
已有部分在ML上做可验证公平性表征的工作,但是存在的问题:在随机给定的一个数据分布上训练一个端到端的模型,这个模型在预测结果上缺乏可验证的公平性。
-
现有公平性上的文献所关注的ML模型,是在一个(非)平衡数据分布上训练模型,在可测量的目标域中通过现有的公平性评估方法来评估模型的性能,所以公平性评估只取决于评估方法的选择,并未考虑方法的验证性。
可验证公平性:在一个公平约束测试分布Q上,其中Q与训练分布P在有界距离内,定义可验证公平性为模型预测损失的最坏情况的上界。
基准利率条件作为测试分布Q的公平约束。
sensitive shifting 敏感偏移:敏感属性与标签的级联分布能改变。
general shifting 一般偏移:包括非敏感属性的条件分布在内的一切都能改变。
群体公平:衡量敏感特征与模型预测之间的独立性。separation【分离性】表明给定目标标签,敏感特征在统计上独立于模型预测。sufficiency【充分性】表明给定模型预测,敏感特征在统计上独立于目标标签。即群体公平要求敏感属性独立于目标标签与模型预测。
个体公平:相似的输入特征会产生相似的输出结果。
本文与先前工作的不同:
- 验证公平性考虑的是端到端ML模型的性能,而非表示学习级别。
- 基于公平约束分布来定义和验证公平性。
- 对于任意一个给定的随机数据分布所训练的黑盒模型,可验证公平性都能计算。
问题1:基准利率条件约束如何编码公平性约束分布?
2. 基于公平约束分布的可验证公平性
定义1 基准利率:给定在X * Y上支持的分布 P P P,敏感属性值 s s s相对于标签 y y y的基准利率为: S S S为敏感属性,[S]为敏感属性所能取的值的集合, s s s为一个敏感属性的一个敏感属性值。 Y Y Y为模型预测结果, y y y为样本label, X X X为样本特征。一个测试样本的基准利率为【敏感属性特征 X s X_s Xs的值为 s s s,预测结果为 y y y的概率】:
定义2 公平性基准利率分布:当且仅当在基准利率产生的某个分布中,对其中的任何两个样本 i i i和 j j j,都具有相同的预测标签 y y y,且都具有敏感属性 S S S中的某个属性值,他们对应的基准利率是相等的,此时这个分布称为具有公平性的基准利率分布:
Demographic Parity:群体公平性评价指标
2.1 可验证公平性
数据生成模型: X o X_o Xo代表非敏感属性特征, X s X_s Xs代表敏感属性特征, Y Y Y代表样本标签。
具有一般偏移的验证公平性: P \mathcal P P为训练集分布, ρ \rho ρ为测试集分布 Q \mathcal Q Q与 P \mathcal P P之间的分布距离界限。对于所有生成的与训练集分布在分布距离 ρ \rho ρ范围内的测试集分布,公平性证明值为:所有测试集分布中的损失值上界的最大值。
真实场景中模型训练集总会因为数据管理和数据收集的限制,所以训练出的模型内在总是存在着不公平。假设我们构造的测试集是理想公平的,我们希望我们的模型在测试的时候并不会编码训练时产生的偏见,因此模型在公平约束分布上的性能表示的是其内在的不公平性。
敏感偏移的可验证公平性:为了避免模型在训练时产生的内在不公性,则在一般偏移的验证公平性下,增加了新的约束。 P s , y P_{s,y} Ps,y与 Q s , y Q_{s,y} Qs,y是 P P P与 Q Q Q的子群【由敏感属性 s s s与 y y y划分】。
为了约束测试集分布 Q Q Q不会太倾斜于敏感属性 X s X_s Xs,因此在敏感偏移中增加额外的约束项:
l o s s loss loss在每一个群每一类中:
上述loss又可转化为ε-DP与ε-EO:
群体均等(Demographic parity,DP):将两个不同群体预测为正类的预测概率差值。
补偿几率(Equalized odds):群体之间假阳性概率(false-positive rates)之差或群体之间真阳性概率(true-positive rates)之差,差值越小则认为模型越公平。
3. 公平性认证框架
3.1 子群分解【核心】
Hellinger距离:度量两个分布之间的距离。值域为【0,1】,越大越相关
整体优化问题:
子群优化问题:
3.2 具有敏感偏移的可验证公平性
3.3 具有一般偏移的可验证公平性
子群分解后的Loss计算:
附录
标量(scalar):一个标量就是一个单独的数(整数或实数),不同于线性代数中研究的其他大部分对象(通常是多个数的数组)。标量通常用斜体的小写字母来表示,例如: x \mathit x x,标量就相当于Python中定义的
x = 1
向量(vector):一个向量表示一组有序排列的数,通过次序中的索引我们能够找到每个单独的数,向量通常用粗体的小写字母表示,例如: x \bf x x,向量中的每个元素就是一个标量,向量中的第i 个元素用$ x_i$ 表示,向量相当于Python中的一维数组
import numpy as np
#行向量
a = np.array([1,2,3,4])
矩阵(matrix):矩阵是一个二维数组,其中的每一个元素由两个索引来决定( A i , j A_{i,j} Ai,j),矩阵通常用加粗斜体的大写字母表示,例如:$ \boldsymbol X$。我们可以将矩阵看做是一个二维的数据表,矩阵的每一行表示一个对象,每一列表示一个特征。在Python中的定义为
import numpy as np
#矩阵
a = np.array([[1,2,3],[4,5,6],[7,8,9]])
张量(tensor):超过二维的数组,一般来说,一个数组中的元素分布在若干维坐标的规则网格中,被称为张量。如果一个张量是三维数组,那么我们就需要三个索引来决定元素的位置( A i , j , k A_{i,j,k} Ai,j,k),张量通常用加粗的大写字母表示,例如: X \bf X X
mport numpy as np
#张量
a = np.array([[[1,2],[3,4]],[[5,6],[7,8]]])
bound 约束找范围
worst case 定边界
如何计算出每个测试样本的r,当r 在bound范围内,预测结果一定大于等于worst case情况,从而具有验证的性质 可验证性质:在预测结果中,有多少样本是符合用户指定bound预测的R。数据分布