LeetCode专题训练--二分查找(上)

目录

前言

一、认识二分法

二、题目详解 

1.1 二分查找

 1.2 猜数字大小

 1.3 搜索插入位置

1.4 山脉数组的峰顶索引

1.5 有效的完全平方数

1.6 x 的平方根 

1.7 第一个错误的版本

1.8 寻找比目标字母大的最小字母

1.9 在排序数组中查找元素的第一个和最后一个位置

1.10 统计有序矩阵中的负数

1.11 搜索二维矩阵

三、总结

---

前言

        二分查找是一个时间效率极高的算法，尤其是面对大量的数据时，其查找效率是极高，时间复杂度是log(n)。主要思想就是不断的对半折叠，每次查找都能除去一半的数据量，直到最后将所有不符合条件的结果都去除，只剩下一个符合条件的结果。

---

一、认识二分法

• 本质：找区间边界，通过满足特定的条件最终找到相应区间，也可以用来找边界（找左右边界时有区别）
• 优点：相比于遍历每个数据的时间复杂度 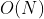，二分算法可以达到  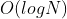的时间复杂度
   

二、题目详解 

1.1 二分查找

题目描述：给定一个 n 个元素有序的(升序)整型数组 nums 和一个目标值 target  ，写一个函数搜索 nums 中的 target，如果目标值存在返回下标，否则返回 -1。

解题思路：这是最基础的二分法入门。

java代码：

public int search(int[] nums, int target) {
    int left = 0;
    int right = nums.length-1;
    int mid = 0;
    while(left<=right){
        // 这里要防止溢出， (left+right)>>1, 会溢出
        mid = left + ((right-left)>>1);
        if(nums[mid] == target){
            // 找到了target
            return mid;
        }else if(nums[mid]>target){
            // 到左边找
            right = mid - 1;
        }else{
            // 到右边找
            left = mid + 1;
        }
    }
    retrun -1;
}

 1.2 猜数字大小

题目描述：每轮游戏，我都会从 1 到 n 随机选择一个数字。 请你猜选出的是哪个数字。如果你猜错了，我会告诉你，你猜测的数字比我选出的数字是大了还是小了。你可以通过调用一个预先定义好的接口 int guess(int num) 来获取猜测结果，返回值一共有 3 种可能的情况(-1，1 或 0)：

   -1：我选出的数字比你猜的数字小 pick < num
    1：我选出的数字比你猜的数字大 pick > num
    0：我选出的数字和你猜的数字一样。恭喜！你猜对了！pick == num
请返回我选出的数字。

解题思路：和第一题类似，利用guess函数的返回值，判断目标值所在的区间。

java代码：

public int guessNumber(int n) {
    int left = 1;
    int right = n;
    int mid = 0;
    while(left <= right){
        mid = left + ((right - left) >> 1);
        if(guess(mid) == 0){
            return mid;
        }else if(guess(mid) == 1){
            left = mid + 1;
        }else{
            right = mid - 1;
        }
    }
    return mid;
}

 1.3 搜索插入位置

题目描述：给定一个排序数组和一个目标值，在数组中找到目标值，并返回其索引。如果目标值不存在于数组中，返回它将会被按顺序插入的位置。请必须使用时间复杂度为   的算法。

解题思路：和前两题不同之处在于，目标值可能不在数组中，当目标值不在数组中时，最后跳出循环时返回待插入的位置。整体解题思路都是一样的，尤其是题目中要求算法时间复杂度为 。可以将第一题数据中的 target 换成16，推理一遍即可。

java代码：

public int searchInsert(int[] nums, int target) {
    int left = 0;
    int right = nums.length-1;
    int mid = 0;
    while(left <= right){
        mid = left + ((right - left)>>1);
        if(nums[mid] == target){
            return mid;
        }else if(nums[mid] > target){
            right = mid - 1;
        }else {
            left = mid + 1;
        }
    }
    return left;
}

1.4 山脉数组的峰顶索引

题目描述：符合下列属性的数组 arr 称为 山脉数组: arr.length >= 3 存在 i（0 < i < arr.length - 1）使得：
     arr[0] < arr[1] < ... arr[i-1] < arr[i]
    arr[i] > arr[i+1] > ... > arr[arr.length - 1]
给你由整数组成的山脉数组 arr ，返回任何满足 arr[0] < arr[1] < ... arr[i - 1] < arr[i] > arr[i + 1] > ... > arr[arr.length - 1] 的下标 i 。

解题思路：这题刚拿到手，看似没有思路，不妨先自己拿一个数组举例：[2, 4, 6, 8, 20, 18, 16, 12, 10]，会发现峰顶的值 arr[i-1] < arr[i] > arr[i+1]，但用于确定峰值的条件，仅需一个就足够了，arr[i] > arr[i+1]；于是这题的本质，就是寻找第一个 arr[i] > arr[i+1] 的值。

 java代码：

public int peakIndexInMountainArray(int[] arr) {
    int left = 0;
    int right = arr.length-1;
    int mid = 0;
    int res = -1;
    while(left <= right){
        mid = left + ((right-left)>>1);
        if(arr[mid] >= arr[mid+1]){
            // 记录当前位置，只能说明arr[i]>arr[i+1], 但是不确定是不是第一个满足这样的arr[i]
            res = mid;
            right = mid - 1;
        }else{
            left = mid + 1;
        }
    }
    return res;
}

1.5 有效的完全平方数

题目描述：给定一个 正整数 num ，编写一个函数，如果 num 是一个完全平方数，则返回 true ，否则返回 false 。进阶：不要 使用任何内置的库函数，如  sqrt 。

解题思路： 考虑使用二分查找来优化方法二中的搜索过程。因为 num 是正整数，所以若正整数 x 满足 x * x = num，则 x 一定满足 1≤x≤num。于是我们可以将 1 和 num 作为二分查找搜索区间的初始边界。

 java代码：

public boolean isPerfectSquare(int num) {
    int left = 1;
    int right = num;
    int mid = 0;
    while(left <= right){
        mid = left + ((right - left) >> 1);
        if(((long)mid  * mid) == num){
            return true;
        }else if(((long)mid*mid)>num){
            right = mid - 1;
        }else{
            left = mid + 1;
        }
    }
    return false;
}

1.6 x 的平方根 

题目描述：给你一个非负整数 x ，计算并返回 x 的 算术平方根 。由于返回类型是整数，结果只保留整数部分 ，小数部分将被舍去 。

注意：不允许使用任何内置指数函数和算符，例如 pow(x, 0.5) 或者 x ** 0.5 。

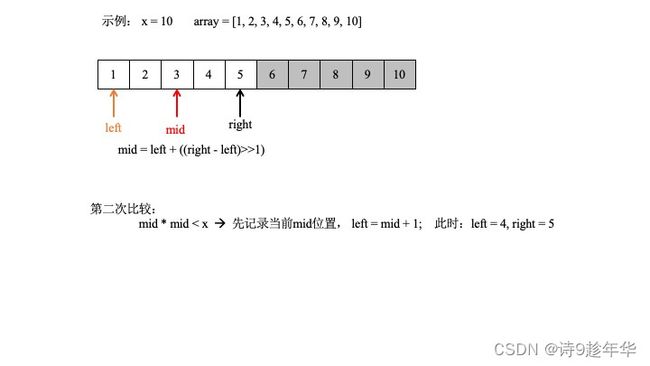
解题思路：有了前面的基础后，读完题目，瞬间就有了思路。其实，可以理解为找到最右的一个数，该数的平方小于等于x；例如：求10的平方根数组部分，1*1 <= 10, 记录，作为备选；2*2 <= 10, 记录，作为备选(此时1就不是备选了)， 3*3<=10, 记录，作为备选(此时2就不是备选了)，4*4=16>10，所以最后一个数的平方值小于等于10的数，则就是结果。只不过，将该方案利用二分的方法进行求解。 

java代码：

 public int mySqrt(int x) {
    int left = 1;
    int right = x;
    int mid = 0;
    int ans = 0;
    while(left <= right){
        mid = left + ((right - left) >> 1);
        if(((long)mid*mid) <= x){
            ans = mid;
            left = mid + 1;
        }else{
            right = mid - 1;
        }
    }
    return ans;
}

1.7 第一个错误的版本

题目描述：你是产品经理，目前正在带领一个团队开发新的产品。不幸的是，你的产品的最新版本没有通过质量检测。由于每个版本都是基于之前的版本开发的，所以错误的版本之后的所有版本都是错的。

假设你有 n 个版本 [1, 2, ..., n]，你想找出导致之后所有版本出错的第一个错误的版本。

你可以通过调用 bool isBadVersion(version) 接口来判断版本号 version 是否在单元测试中出错。实现一个函数来查找第一个错误的版本。你应该尽量减少对调用 API 的次数。

解题思路：有了上一题的经验，这题就一样处理了。

java代码：

 public int firstBadVersion(int n) {
    int left = 1;
    int right = n;
    int mid = 0;
    int ans = 0;
    while(left <= right){
        mid = left + ((right - left)>>1);
        if(isBadVersion(mid)){
            ans = mid;
            right = mid - 1;
        }else{
            left = mid + 1;
        }
    }
    return ans;
}

1.8 寻找比目标字母大的最小字母

题目描述：给你一个排序后的字符列表 letters ，列表中只包含小写英文字母。另给出一个目标字母 target，请你寻找在这一有序列表里比目标字母大的最小字母。

在比较时，字母是依序循环出现的。举个例子：

如果目标字母 target = 'z' 并且字符列表为 letters = ['a', 'b']，则答案返回 'a'

解题思路：有了上一题的经验，这题就类似处理了。只不过，需要注意的是，当target为z的时候，直接返回数组中第一个元素即可。

java代码：

public char nextGreatestLetter(char[] letters, char target) {
    // 如果目标字母 target = 'z', 则返回数组中第一个即可。因为数组不为空，不做为空判断。
    if(target == 'z'){
        return letters[0];
    }
    // 常规二分法逻辑。
    int left = 0;
    int right = letters.length-1;
    int mid = 0;
    int ans = 0;
    while(left <= right){
        mid = left + ((right-left)>>1);
        // 用大于逻辑
        if(letters[mid] > target){
            ans = mid;
            right = mid - 1;
        }else{
            left = mid + 1;
        }
    }
    return letters[ans];
}

1.9 在排序数组中查找元素的第一个和最后一个位置

做此题前，先补充两个小题：

题目一：找出数组array中大于等于num最左的位置。

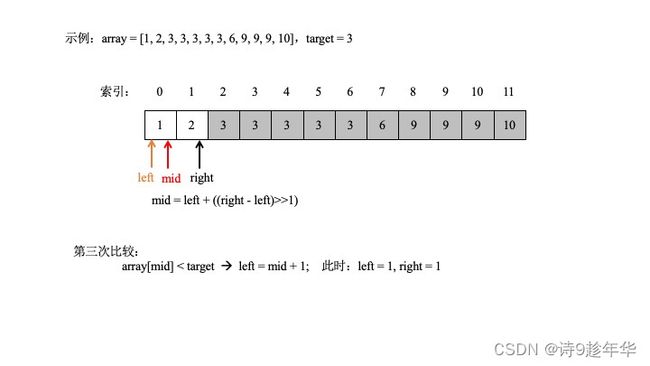
示例：array = [1, 2, 3, 3, 3, 3, 3, 6, 9, 9, 9, 10]，target = 3；答案是2

 

题目二：找出数组array中小于等于num最右的位置。

示例：array = [1, 2, 3, 3, 3, 3, 3, 6, 9, 9, 9, 10]，target = 3；答案是6 。同理，当小于等于num时，记录当时的位置。具体过程不在叙述。

题目描述：给你一个按照非递减顺序排列的整数数组 nums，和一个目标值 target。请你找出给定目标值在数组中的开始位置和结束位置。

如果数组中不存在目标值 target，返回 [-1, -1]。你必须设计并实现时间复杂度为 O(log n) 的算法解决此问题。

解题思路：有了上述两个小题的铺垫，这题要在  时间复杂度完成，其实就这个两个小题分别 计算一次就能得到。

java代码：

public int[] searchRange(int[] nums, int target) {
    if(nums == null || nums.length < 1){
        return new int[]{-1, -1};
    }
    return new int[]{firstIndex(nums, target), lastIndex(nums, target)};
}

public int firstIndex(int[] nums, int target){
    int left = 0;
    int right = nums.length-1;
    int mid = 0;
    int ans = 0;
    while(left <= right){
        mid = left + ((right - left)>>1);
        if(nums[mid] >= target){
            ans = mid;
            right = mid - 1;         
        }else{
            left = mid + 1;
        }
    }
    // 说明数组中不存在该target
    if(nums[ans] != target){
        return -1;
    }
    return ans;
}

public int lastIndex(int[] nums, int target){
    int left = 0;
    int right = nums.length-1;
    int mid = 0;
    int ans = 0;
    while(left <= right){
        mid = left + ((right - left)>>1);
        if(nums[mid] <= target){
            ans = mid;
            left = mid + 1;
        }else{
            right = mid - 1;
        }
    }
    // 说明数组中不存在该target
    if(nums[ans] != target){
        return -1;
    }
    return ans;
}

尽管我写的代码，通过了，但是有两个很明显的问题；一是重复了，二是在处理特定场景时，多添加一个次判断。随后，参考了更加优雅的代码：

public int[] searchRange(int[] nums, int target) {
    int leftIdx = binarySearch(nums, target, true);
    int rightIdx = binarySearch(nums, target, false) - 1;
    if (leftIdx <= rightIdx && rightIdx < nums.length && nums[leftIdx] == target && nums[rightIdx] == target) {
        return new int[]{leftIdx, rightIdx};
    } 
    return new int[]{-1, -1};
}

public int binarySearch(int[] nums, int target, boolean lower) {
    int left = 0, right = nums.length - 1, ans = nums.length;
    while (left <= right) {
        int mid = (left + right) / 2;
        if (nums[mid] > target || (lower && nums[mid] >= target)) {
            right = mid - 1;
            ans = mid;
        } else {
            left = mid + 1;
        }
    }
    return ans;
}

1.10 统计有序矩阵中的负数

题目描述：给你一个 m * n 的矩阵 grid，矩阵中的元素无论是按行还是按列，都以非递增顺序排列。 请你统计并返回 grid 中 负数 的数目。

解题思路：首先遍历矩阵的每一行，然后利用二分法查找到该行从前往后的第一个负数，则后面的都是负数。

java代码：

public int countNegatives(int[][] grid) {
    int row = grid.length;
    int col = grid[0].length;
    if(grid[row-1][col-1]>=0){
        return  0;
     }
    // 利用二分法遍历每一行
    int sum = 0;
    for(int i = 0; i < row; i++){
        int left = 0;
        int right = grid[i].length - 1;
        int mid = 0;
        int index = right+1;
        while(left <= right){
            mid = left + ((right - left)>>1);
            if(grid[i][mid] >= 0){
                left = mid + 1;
            }else{
                index = mid;
                right = mid - 1;
            }
        }
        // 得到的index，就是第一个负数的位置
        // 负数的个数
        sum +=grid[i].length-index;
    }    
    return sum;
}

1.11 搜索二维矩阵

题目描述：编写一个高效的算法来判断 m x n 矩阵中，是否存在一个目标值。该矩阵具有如下特性：每行中的整数从左到右按升序排列。每行的第一个整数大于前一行的最后一个整数

解题思路：

方法一：基于坐标来查找的算法。

方法二：基于二分法。首先遍历矩阵的每一行，然后利用二分法查找到该行从前往后的第一个负数，则后面的都是负数。

java代码：

public boolean searchMatrix(int[][] matrix, int target) {
    // 方法一：
    // int row = 0;
    // int col = matrix[0].length-1;
    // while(row < matrix.length && col >= 0){
    //     if(matrix[row][col] > target){
    //         col--;
    //     }else if (matrix[row][col] < target){
    //         row++;
    //     }else{
    //         return true;
    //     }
    // }
    // return false;

    // 二分法：
    int row = matrix.length;
    int col = matrix[0].length;
    int left = 0;
    int right = row * col-1;
    int mid = 0;
    while(left <= right){
        mid = left + ((right - left)>>1);
        if(matrix[mid / col][mid % col] > target){
            right = mid - 1;
        } else if(matrix[mid / col][mid % col] < target){
            left = mid + 1;
        }else{
            return true;
        }
    }
    return false;
}

来源：力扣（LeetCode）
链接：https://leetcode.cn/problems/search-a-2d-matrix
著作权归领扣网络所有。商业转载请联系官方授权，非商业转载请注明出处。

三、总结

使用二分法，我们要按照以下两个步骤：

1. 我们要确定一个区间[L，R]

2. 我们要找到一个性质，并且该性质满足一下两点：
        ①满足二段性(对某一范围内的数据，存在一个临界点，使得临界点某一侧的所有数据都满足某一性质，另一侧的所有数据都不满足这一性质，就称这一范围内的数据具有二段性。)
        ②答案是二段性的分界点。