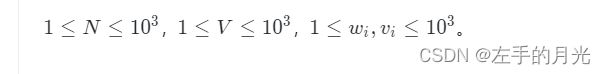蓝桥杯带刷,带刷!!!
A:::::::::::::::::::::::::::::::::::m计划(双指针,滑动窗口,倍增)
题目描述
小明是个鹅卵石收藏者,从小到大他一共收藏了 nn 块鹅卵石,编号分别为 1∼n,价值分别为 a1,a2,⋯,an。
这天他乘船准备去往蓝桥王国,然而天有不测风云,小明所在的海域下起了暴雨。
很快小明船上的积水越来越多,为了防止沉船,小明不得不选择若干块他收藏的鹅卵石丢弃。
小明制定了一套名为m计划的选择方案,其内容如下:
- 对于任意区间 [i,i + m - 1]丢弃价值最小的鹅卵石i∈[1,n−m+1]。
- 对于一块鹅卵石,它在 m 计划中是可以被丢弃多次的。
请你输出将被小明丢弃的鹅卵石的价值。
输入描述
输入第 1 行包含两个正整数 n,m。
接下来一行包含 n 个正整 a1,a2,⋯,an,表示鹅卵石的价值。
1≤m≤n≤5×10的5次方,0≤ai≤10的9次方。
输出描述
输出共 n−m+1 行,每行输出一个整数,第 i 行输出整数的含义为 ai,ai+1,⋯,ai+m−1 的最小值。
输入输出样例
示例 1
输入
5 3
5 3 2 4 1
输出
2
2
1#include
using namespace std;
int n,m;
int a[500005];
struct node{
int xiabiao;
int min1;
};
node check1(int x,int y){
node ans1;
ans1.xiabiao=0;
ans1.min1=1000000;
for(int i=x;i<=y;i++){
if(a[i]<=ans1.min1){
ans1.min1=a[i];
ans1.xiabiao=i;
}
}
return ans1;
}
bool check2(int l,int r,int x){
return x>=l&&x<=r;
}
int main(){
cin>>n>>m;
for(int i=1;i<=n;i++){
cin>>a[i];
}
node mm=check1(1,m);
int l=2,r=m+1;
cout<=a[r]){
mm.min1=a[r];
mm.xiabiao=r;
}
}else{
mm=check1(l,r);
}
cout< B:::::::::::::::::::::::::::::::::::长草(BFS)
题目描述
小明有一块空地,他将这块空地划分为 n 行 m 列的小块,每行和每列的长度都为 1。
小明选了其中的一些小块空地,种上了草,其他小块仍然保持是空地。
这些草长得很快,每个月,草都会向外长出一些,如果一个小块种了草,则它将向自己的上、下、左、右四小块空地扩展,
这四小块空地都将变为有草的小块。请告诉小明,k 个月后空地上哪些地方有草。
输入描述
输入的第一行包含两个整数 n,m。
接下来 n 行,每行包含 m 个字母,表示初始的空地状态,字母之间没有空格。如果为小数点,表示为空地,如果字母为 g,表示种了草。
接下来包含一个整数 k。 其中,2≤n,m≤1000,1≤k≤1000。
输出描述
输出 n 行,每行包含 mm 个字母,表示 k 个月后空地的状态。如果为小数点,表示为空地,如果字母为 g,表示长了草。
输入输出样例
示例
输入
4 5
.g...
.....
..g..
.....
2
输出
gggg.
gggg.
ggggg
.ggg.
运行限制
- 最大运行时间:1s
- 最大运行内存: 256M
#include
#include
using namespace std;
int n,m,k;
char a[1005][1005];
struct node{
int x,y;
int su;
node(int xx,int yy,int suu){
x=xx;
y=yy;
su=suu;
}
};
queue h;
bool check(int x,int y){
return x>=1&&x<=n&&y>=1&&y<=m;
}
int f[4][2]={{1,0},{-1,0},{0,-1},{0,1}};
int main(){
cin>>n>>m;
for(int i=1;i<=n;i++){
for(int j=1;j<=m;j++){
cin>>a[i][j];
if(a[i][j]=='g'){
h.push(node(i,j,0));
}
}
}
cin>>k;
while(!h.empty()){
node j=h.front();
h.pop();
for(int i=0;i<4;i++){
int tx=j.x+f[i][0];
int ty=j.y+f[i][1];
if(check(tx,ty) && a[tx][ty]=='.' && j.su+1<=k){
a[tx][ty]='g';
h.push(node(tx,ty,j.su+1));
}
}
}
for(int i=1;i<=n;i++){
for(int j=1;j<=m;j++){
cout< C:::::::::::::::::::::::::::::::::::带分数(全排列)
题目描述
100 可以表示为带分数的形式:100 = 3 + 69258 / 714
还可以表示为:100 = 82 + 3546 / 197
注意特征:带分数中,数字 1~9 分别出现且只出现一次(不包含 0 )。
类似这样的带分数,100 有 11 种表示法。
输入描述
从标准输入读入一个正整数 (N<1000×1000)。
输出描述
程序输出该数字用数码 1~9 不重复不遗漏地组成带分数表示的全部种数。
注意:不要求输出每个表示,只统计有多少表示法!
输入输出样例
示例
输入
100
输出
11
运行限制
- 最大运行时间:3s
- 最大运行内存: 64M
#include
#include
using namespace std;
int n;
long long ans;
int a[9]={1,2,3,4,5,6,7,8,9};
int he(int l,int r){
int ans1=0;
for(int i=l;i<=r;i++){
ans1=ans1*10+a[i];
}
return ans1;
}
int main(){
cin>>n;
while(next_permutation(a,a+9)){
for(int i=0;i<7;i++){
for(int j=i+1;j<8;j++){
int a=he(0,i);
int b=he(i+1,j);
int c=he(j+1,8);
if(a*c+b==n*c){
ans++;
}
}
}
}
cout< D:::::::::::::::::::::::::::::::::::合根植物(并查集)
题目描述
w 星球的一个种植园,被分成 m×n 个小格子(东西方向 m 行,南北方向 n 列)。每个格子里种了一株合根植物。
这种植物有个特点,它的根可能会沿着南北或东西方向伸展,从而与另一个格子的植物合成为一体。
如果我们告诉你哪些小格子间出现了连根现象,你能说出这个园中一共有多少株合根植物吗?
输入描述
第一行,两个整数 m,n,用空格分开,表示格子的行数、列数(1≤m,n≤1000)。
接下来一行,一个整数 k (0≤k≤105 ),表示下面还有 k 行数据。
接下来 k 行,每行两个整数 a,b,表示编号为 a 的小格子和编号为 b 的小格子合根了。
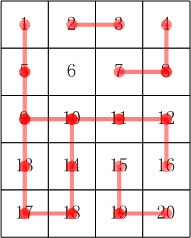
格子的编号一行一行,从上到下,从左到右编号。
比如:5×4 的小格子,编号:
1 2 3 4
5 6 7 8
9 10 11 12
13 14 15 16
17 18 19 20
输出描述
输出植物数量。
输入输出样例
示例
输入
5 4
16
2 3
1 5
5 9
4 8
7 8
9 10
10 11
11 12
10 14
12 16
14 18
17 18
15 19
19 20
9 13
13 17
输出
5
样例说明
其合根情况参考下图:
运行限制
- 最大运行时间:2s
- 最大运行内存: 256M
#include
#include
using namespace std;
int m,n,k;
int vis[1000005];
int fa[1000005];
int find(int x){
if(fa[x]==x) return x;
return fa[x]=find(fa[x]);
}
int ans;
void jiaru(int x,int y){
int tx=find(x);
int ty=find(y);
if(tx!=ty){
fa[tx]=ty;
}
}
int main(){
cin>>m>>n>>k;
for(int i=0;i<=n*m;i++){
fa[i]=i;
}
for(int i=0;i>a>>b;
jiaru(a,b);
}
for(int i=1;i<=n*m;i++){
vis[find(i)]=1;
}
for(int i=1;i<=n*m;i++){
if(vis[i]){
ans+=1;
}
}
cout< E:::::::::::::::::::::::::::::::::::修建公路(最小生成树,并查集)
题目描述
LL 城一共有 N 个小区。
小明是城市建设的规划者,他计划在城市修 M 条路,每修建一条路都要支付工人们相应的工钱(需要支付的工钱 = 路的长度)。
然而小明所拿到的经费并不够支付修建 M 条路的工钱,于是迫于无奈,他只能将计划改变为修建若干条路,使得 N 个小区之间两两联通。
小明希望尽量剩下更多的经费投入到别的项目中,因此请你通过程序帮他计算出完成计划所需的最低开销。
输入描述
输入第一行包含三个正整数N,M。
第 2 到 M+1 行每行包含三个正整数 u,v,w,表示 u↔v 之间存在一条距离为 w 的路。
输出描述
输出占一行,包含一个整数,表示完成计划所需的最低开销。
若无法完成计划,则输出 -1−1。
输入输出样例
示例 1
输入
5 6
1 2 2
1 3 7
1 4 6
2 3 1
3 4 3
3 5 2
输出
8
运行限制
- 最大运行时间:3s
- 最大运行内存: 256M、
#include
#include
using namespace std;
int n,m;
int fa[100005];
int find(int x){
if(fa[x]==x) return x;
return fa[x]=find(fa[x]);
}
struct node{
int qi,zhong;
int juli;
};
bool cmp(node x,node y){
return x.juli>n>>m; //n个城市,m个规划
for(int i=1;i<=n;i++){
fa[i]=i;
}
for(int i=1;i<=m;i++){
cin>>g[i].qi>>g[i].zhong>>g[i].juli;
}
sort(g+1,g+m+1,cmp);
for(int i=1;i<=m;i++){
int tx=find(g[i].qi);
int ty=find(g[i].zhong);
if(tx!=ty){
ans+=g[i].juli;
fa[tx]=ty;
}
}
int w=find(1);
for(int i=1;i<=n;i++){
if(w!=find(i)){
cout<<-1;
return 0;
}
}
cout< F:::::::::::::::::::::::::::::::::::小明的背包2(完全背包)
题目描述
小明有一个容量为 V 的背包。
这天他去商场购物,商场一共有 N 种物品,第 ii 种物品的体积为 wi,价值为 vi,每种物品都有无限多个。
小明想知道在购买的物品总体积不超过 V 的情况下所能获得的最大价值为多少,请你帮他算算。
输入描述
输入第 1 行包含两个正整数 N,V,表示商场物品的数量和小明的背包容量。
第 2∼N+1 行包含 2 个正整数w,v,表示物品的体积和价值。
输出描述
输出一行整数表示小明所能获得的最大价值。
输入输出样例
示例 1
输入
5 20
1 6
2 5
3 8
5 15
3 3
输出
120#include
#include
using namespace std;
int n,v;
int wi[1005];
int vi[1005];
int dp[1005][1005];
int main(){
cin>>n>>v;
for(int i=1;i<=n;i++){
cin>>wi[i]>>vi[i]; //体积和价值
}
for(int i=1;i<=n;i++){
for(int j=1;j<=v;j++){
dp[i][j]=dp[i-1][j];
if(j>=wi[i]){
dp[i][j]=max(dp[i-1][j],dp[i][j-wi[i]]+vi[i]);
}
}
}
cout< G:::::::::::::::::::::::::::::::::::作物杂交(搜索)
题目描述
作物杂交是作物栽培中重要的一步。已知有 N 种作物 (编号 1 至 N),第 i 种作物从播种到成熟的时间为 Ti。作物之间两两可以进行杂交,杂交时间取两种中时间较长的一方。如作物 A 种植时间为 5 天,作物 B 种植时间为 7 天,则 AB 杂交花费的时间为 7 天。作物杂交会产生固定的作物,新产生的作物仍然属于 N 种作物中的一种。
初始时,拥有其中 M 种作物的种子 (数量无限,可以支持多次杂交)。同时可以进行多个杂交过程。求问对于给定的目标种子,最少需要多少天能够得到。
如存在 4 种作物 ABCD,各自的成熟时间为 5 天、7 天、3 天、8 天。初始拥有 AB 两种作物的种子,目标种子为 D,已知杂交情况为 A × B → C,A × C → D。则最短的杂交过程为:
第 1 天到第 7 天 (作物 B 的时间),A × B → C。
第 8 天到第 12 天 (作物 A 的时间),A × C → D。
花费 12 天得到作物 D 的种子。
输入描述
输入的第 1 行包含 4 个整数 N,M,K,T,NN 表示作物种类总数 (编号 1 至 N),MM 表示初始拥有的作物种子类型数量,KK 表示可以杂交的方案数,TT 表示目标种子的编号。
第 2 行包含 N 个整数,其中第 ii 个整数表示第 ii 种作物的种植时间 Ti (1≤Ti≤100)。
第 3 行包含 M 个整数,分别表示已拥有的种子类型 (1≤Kj≤M),Kj 两两不同。
第 4 至 K + 3 行,每行包含 3 个整数 A,B,C,表示第 A 类作物和第 B 类作物杂交可以获得第 C 类作物的种子。
其中,1≤N≤2000,2≤M≤N,1≤K≤105,1≤T≤N, 保证目标种子一定可以通过杂交得到。
输出描述
输出一个整数,表示得到目标种子的最短杂交时间。
输入输出样例
示例
输入
6 2 4 6
5 3 4 6 4 9
1 2
1 2 3
1 3 4
2 3 5
4 5 6
输出
16
样例说明
第 1 天至第 5 天,将编号 1 与编号 2 的作物杂交,得到编号 3 的作物种子。
第 6 天至第 10 天,将编号 1 与编号 3 的作物杂交,得到编号 4 的作物种子。
第 6 天至第 9 天,将编号 2 与编号 3 的作物杂交,得到编号 5 的作物种子。
第 11 天至第 16 天,将编号 4 与编号 5 的作物杂交,得到编号 6 的作物种子。
总共花费 16 天。
运行限制
| 语言 | 最大运行时间 | 最大运行内存 |
|---|---|---|
| C++ | 2s | 256M |
| C | 2s | 256M |
| Java | 3s | 256M |
| Python3 | 10s | 256M |
#include
#include
using namespace std;
const int maxn=0x3f3f3f3f;
int tim[2010];
int dp[2010];
vector > zajiao[2010];
int f(int n){
if (dp[n]!=maxn) return dp[n];
for (int i=0;i>n>>m>>k>>t;
for (int i=1;i<=n;++i){
cin>>tim[i];
}
for (int i=1;i<=m;++i){
int j;
cin>>j;
dp[j]=0;
}
for (int i=1;i<=k;++i){
int a,b,c;
cin>>a>>b>>c;
zajiao[c].push_back(make_pair(a, b));
}
f(t);
cout< H:::::::::::::::::::::::::::::::::::序列求和(DFS,唯一分解定理)
题目描述
本题为填空题,只需要算出结果后,在代码中使用输出语句将所填结果输出即可。
学习了约数后,小明对于约数很好奇,他发现,给定一个正整数 tt,总是可以找到含有 tt 个约数的整数。小明对于含有 tt 个约数的最小数非常感兴趣,并把它定义为 S_tSt 。
例如S1=1,S2=2,S3=4,S4=6,⋅⋅⋅ 。
现在小明想知道,前 60 个 Si 的和是多少?即 S1+S2+⋅⋅⋅+S60 是多少?
运行限制
- 最大运行时间:1s
- 最大运行内存: 128M
#include
#include
#include
using namespace std;
vector m;
int su[100000];
bool check(long long x){
if(x==1){
return false;
}
if(x==2){
return true;
}
for(int i=2;i*i<=x;i++){
if(x%i==0){
return false;
}
}
return true;
}
long long pow1(long long a,long long b){
long long ans=1;
while(b){
if(b&1) ans=ans*a;
b/=2;
a*=a;
}
return ans;
}
long long ans;
long long res1=1e18;
long long dfs(long long x,vectorg)
{
if(check(x)||x==1)return pow1(2,x-1);
for(long long i=2;i*i<=x;i++)
{
if(x%i==0)
{
long long t=x/i;
g.push_back(i);
vectortmp=g;
tmp.push_back(t);
sort(tmp.begin(),tmp.end(),greater());
long long s=1;
for(int j=0;j I:::::::::::::::::::::::::::::::::::青蛙跳杯子(BFS)
题目描述
XX 星球的流行宠物是青蛙,一般有两种颜色:白色和黑色。
XX 星球的居民喜欢把它们放在一排茶杯里,这样可以观察它们跳来跳去。
如下图,有一排杯子,左边的一个是空着的,右边的杯子,每个里边有一只青蛙。
∗WWWBBB
其中,W 字母表示白色青蛙,B 表示黑色青蛙,*∗ 表示空杯子。
X 星的青蛙很有些癖好,它们只做 3 个动作之一:
-
跳到相邻的空杯子里。
-
隔着 1 只其它的青蛙(随便什么颜色)跳到空杯子里。
-
隔着 2 只其它的青蛙(随便什么颜色)跳到空杯子里。
对于上图的局面,只要 1 步,就可跳成下图局面:
WWW∗BBB
本题的任务就是已知初始局面,询问至少需要几步,才能跳成另一个目标局面。
输入描述
输入为 2 行,2 个串,表示初始局面和目标局面。我们约定,输入的串的长度不超过 15。
输出描述
输出要求为一个整数,表示至少需要多少步的青蛙跳。
输入输出样例
示例
输入
*WWBB
WWBB*
输出
2
运行限制
- 最大运行时间:1s
- 最大运行内存: 256M
#include
#include
#include
#include J:::::::::::::::::::::::::::::::::::剪格子(DFS)
题目描述
如下图所示,3 x 3 的格子中填写了一些整数。
我们沿着图中的红色线剪开,得到两个部分,每个部分的数字和都是 60。
本题的要求就是请你编程判定:对给定的 m×n 的格子中的整数,是否可以分割为两个部分,使得这两个区域的数字和相等。
如果存在多种解答,请输出包含左上角格子的那个区域包含的格子的最小数目。
如果无法分割,则输出 0。
输入描述
输入描述
程序先读入两个整数 m,n 用空格分割 (m,n<10),表示表格的宽度和高度。
接下来是 n 行,每行 m 个正整数,用空格分开。每个整数不大于 104。
输出描述
在所有解中,包含左上角的分割区可能包含的最小的格子数目。
输入输出样例
示例
输入
3 3
10 1 52
20 30 1
1 2 3
输出
3
运行限制
- 最大运行时间:5s
- 最大运行内存: 64M
#include
using namespace std;
int a[15][15];
int n,m;
int sum;
int he;
int ans=1e9;
bool vis[15][15];
int aa[4][2]={{1,0},{-1,0},{0,-1},{0,1}};
bool check(int x,int y){
return x>=0&&x<=n&&y>=0&&y<=m;
}
void dfs(int x,int y,int g){
if(g>=ans){
return;
}
if(he==sum/2){
ans=min(ans,g);
}
for(int i=0;i<4;i++){
int tx=x+aa[i][0];
int ty=y+aa[i][1];
if(check(tx,ty) && !vis[tx][ty]){
vis[tx][ty]=1;
he+=a[tx][ty];
dfs(tx,ty,g+1);
he-=a[tx][ty];
vis[tx][ty]=0;
}
}
}
int main(){
cin>>m>>n;
for(int i=1;i<=n;i++){
for(int j=1;j<=m;j++){
int x=0;
cin>>x;
a[i][j]=x;
sum+=x;
}
}
if(sum%2==1){
cout<<0;
return 0;
}
vis[1][1]=1;
he=a[1][1];
dfs(1,1,1);
cout<