(CVPR-2022)视觉转换器与变形注意力

视觉转换器与变形注意力

paper题目：Vision Transformer with Deformable Attention

paper是清华发表在CVPR 2022的工作

paper地址：链接

Abstract

Transformer最近在各种视觉任务中表现出了卓越的表现。大的，有时甚至是全局的感受野赋予Transformer模型比CNN模型具有更高的表示能力。然而，单纯扩大感受野也会引起一些问题。一方面，使用密集注意力(例如在ViT中)会导致过多的内存和计算成本，并且特征可能会受到超出感兴趣区域的无关部分的影响。另一方面，在PVT或Swin Transformer中采用的稀疏注意力是数据不可知的，可能会限制对长期关系建模的能力。为了缓解这些问题，我们提出了一种新的可变形的自注意力模块，其中键和值对在自注意力中的位置以数据依赖的方式选择。这种灵活的方案使自注意力模块能够专注于相关区域，并捕获更多信息特征。在此基础上，我们提出了变形注意力转换器，这是一种适用于图像分类和密集预测任务的具有变形注意力的通用骨干模型。大量的实验表明，我们的模型在综合基准上取得了持续改进的结果。代码可从链接获得。

1. Introduction

Transformer[29]最初是为了解决自然语言处理任务而引入的。近年来，它在计算机视觉领域显示出巨大的潜力[11,23,31]。先驱工作Vision Transformer [11] (ViT)堆叠多个Transformer块来处理不重叠的图像patch(即视觉令牌)序列，从而形成用于图像分类的无卷积模型。与CNN模型相比[17,18]，基于transformer的模型具有更大的感受野，并且擅长建模长期依赖关系，被证明在大量训练数据和模型参数的情况下具有更好的性能。然而，视觉识别中的多余注意力是一把双刃剑，存在诸多弊端。具体来说，每个查询patch需要参与的键数过多会导致计算成本高、收敛速度慢，并增加过拟合的风险。

为了避免过多的注意力计算，现有的工作[6、10、23、31、37、40]利用精心设计的有效注意力模式来降低计算复杂度。作为其中两种具有代表性的方法，Swin Transformer [23] 采用基于窗口的局部注意力来限制局部窗口中的注意力，而 Pyramid Vision Transformer (PVT) [31] 对键和值特征图进行下采样以节省计算量。虽然有效，但手工制作的注意力模式与数据无关，可能不是最佳的。很可能相关的键/值被删除，而不太重要的键/值仍然保留。

理想情况下，人们会期望给定查询的候选键/值集是灵活的并且能够适应每个单独的输入，这样可以缓解手工制作的稀疏注意力模式中的问题。事实上，在 CNN 的文献中，学习卷积滤波器的可变形感受野已被证明可以有效地在数据依赖的基础上选择性地关注更多信息区域 [8]。最著名的工作是可变形卷积网络 [8]，它在许多具有挑战性的视觉任务上取得了令人印象深刻的结果。这促使我们探索 Vision Transformers 中的可变形注意力模式。然而，这个想法的天真实现会导致不合理的高内存/计算复杂度：可变形偏移引入的开销是patch数量的二次方。因此，尽管最近的一些工作 [7, 39, 44] 研究了 Transformers 中的可变形机制的想法，但由于高计算成本。相反，它们的可变形机制要么被用于检测头[44]，要么被用作预处理层来为后续的骨干网络[7]采样patch。

在本文中，我们提出了一个简单高效的可变形自注意力模块。配备了它，我们为各种视觉任务设计了一个名为可变形注意力转换器 (DAT) 的强大主干。与 DCN 学习整个特征图中不同像素的不同偏移量不同，我们建议学习几组所有查询共享的采样偏移量，以将键和值移动到重要区域（如图 1（d）所示），基于根据 [3, 42] 中的观察，全局注意力通常会导致不同查询的注意力模式几乎相同。这种设计既保持了线性空间复杂度，又为 Transformer 骨干引入了可变形的注意力模式。具体来说，对于每个注意力模块，参考点首先生成为均匀网格，这些网格在输入数据中是相同的。然后，偏移网络将所有查询特征作为输入，并为所有参考点生成相应的偏移量。通过这种方式，候选键/值被转移到重要区域，从而以更高的灵活性和效率增强原始自注意力模块，以捕获更多信息特征。

总而言之，我们的贡献如下：我们提出了第一个用于视觉识别的可变形自注意力主干，其中数据依赖的注意力模式赋予了更高的灵活性和效率。在 ImageNet [9]、ADE20K [41] 和 COCO [22] 上进行的大量实验表明，我们的模型始终优于包括 Swin Transformer 在内的竞争基线，在图像分类的 top-1 准确度上领先 0.7，在语义的 mIoU 上领先 1.2分割，1.1 关于 box AP 和 mask AP 的目标检测。在小型和大型物体上的优势更加明显，差距为 2.1。

2. Related Work

转换器视觉骨干。自从引入 ViT [11] 以来，改进 [6、10、23、24、31、37、40] 一直专注于学习多尺度特征以实现密集的预测任务和高效的注意力机制。这些注意力机制包括窗口注意力 [10、23]、全局标记 [6、19、27]、焦点注意力 [37] 和动态标记大小 [32]。最近，基于卷积的方法被引入到 Vision Transformer 模型中，其中存在的研究重点是用卷积操作补充 Transformer 模型以引入额外的归纳偏差。 CvT [34] 在标记化过程中采用卷积，并利用步长卷积来降低自注意力的计算复杂度。 ViT with convolutional stem [36] 提出在早期加入卷积以实现更稳定的训练。 CSwin Transformer [10] 采用基于卷积的位置编码技术，并对下游任务进行了改进。许多这些基于卷积的技术都可以潜在地应用于 DAT 之上，以进一步提高性能。

可变形 CNN 和注意力。可变形卷积 [8, 43] 是一种强大的机制，可以处理以输入数据为条件的灵活空间位置。最近它已被应用于 Vision Transformers [7,39,44]。可变形 DETR [44] 通过为 CNN 主干顶部的每个查询选择少量键来提高 DETR [4] 的收敛性。它的可变形注意力不适合用于特征提取的视觉主干，因为缺少键限制了表示能力。此外，可变形 DETR 中的注意力来自简单学习的线性投影，并且键不在查询令牌之间共享。 DPT [7] 和 PS-ViT [39] 构建可变形模块来改进视觉标记。具体来说，DPT 提出了一个可变形的patch嵌入来改进跨阶段的patch，PS-ViT 在 ViT 主干之前引入了一个空间采样模块来改进视觉标记。它们都没有将可变形注意力纳入视觉骨干。相比之下，我们的可变形注意力采用强大而简单的设计来学习一组在视觉标记之间共享的全局键，并且可以用作各种视觉任务的通用骨干。我们的方法也可以看作是一种空间自适应机制，已在各种工作中证明是有效的 [15, 33]。

3. Deformable Attention Transformer

3.1. Preliminaries

---

我们首先回顾最近的 Vision Transformers 中的注意力机制。以展平特征图$x\in {\mathbb{R}}^{N\times C}$作为输入，具有$M$个头的多头自注意力 (MHSA) 块表示为
$$\begin{array}{rl}& q=x{W}_q,k=x{W}_k,v=x{W}_v,(1)\\ & z^{(m)}=\sigma \left(q^{(m)}{k}^{(m)\top }/\sqrt{d}\right)v^{(m)},m=1,\dots ,M,(2)\\ & z=\text{ Concat }\left(z^{(1)},\dots ,z^{(M)}\right)W_o,(3)\end{array}$$
其中$\sigma (\cdot )$表示softmax函数，$d=C/M$是每个头的维度。 $z^{(m)}$表示第$m$个注意力头的嵌入输出，$q^{(m)},k^{(m)},v^{(m)}\in$ ${\mathbb{R}}^{N\times d}$分别表示查询、键和值嵌入。$W_q,W_k,W_v,W_o\in {\mathbb{R}}^{C\times C}$是投影矩阵。为了构建 Transformer 块，通常采用具有两个线性变换和GELU激活的 MLP 块来提供非线性。

使用归一化层和恒等映射，第$l$个 Transformer 块表示为
$$\begin{array}{rl}{z}_l^{\prime }& =\mathrm{MHSA}\left(\mathrm{LN}\left(z_{l-1}\right)\right)+z_{l-1},(4)\\ z_l& =\mathrm{MLP}\left(\mathrm{LN}\left(z_l^{\prime }\right)\right)+z_l^{\prime },(5)\end{array}$$
其中 LN 是层归一化 [1]。

3.2. Deformable Attention

---

现有的分层 Vision Transformers，特别是 PVT [31] 和 Swin Transformer [23] 试图解决过度关注的挑战。前者的下采样技术导致严重的信息丢失，而后者的 shiftwindow attention 导致感受野的增长缓慢得多，这限制了对大型目标建模的潜力。因此，需要依赖数据的稀疏注意力来灵活地对相关特征进行建模，从而导致在 DCN [8] 中首次提出的可变形机制。然而，将 DCN 应用于 Transformer 模型是一个非常重要的问题。在 DCN 中，特征图上的每个元素单独学习其偏移量，其中在$H\times W\times C$特征图上的$3\times 3$可变形卷积具有$9H\mathrm{WC}$的空间复杂度。如果我们直接在注意力模块中应用相同的机制，空间复杂度将急剧上升到$N_{\mathrm{q}}{N}_{\mathrm{k}}C$，其中$N_{\mathrm{q}},N_{\mathrm{k}}$是查询和键的数量，通常与特征图大小$HW$具有相同的尺度，带来近似双二次的复杂度。尽管 Deformable DETR [44] 已经设法通过在每个尺度上设置较少数量的$N_{\mathrm{k}}=4$的键来减少这种开销并且作为检测头工作得很好，但由于不可接受的信息丢失（参见附录中的详细比较）。与此同时，[3, 42] 中的观察结果表明，不同的查询在视觉注意力模型中具有相似的注意力图。因此，我们选择一个更简单的解决方案，为每个查询共享移位键和值，以实现有效的权衡。

具体来说，我们提出了可变形注意力机制，以在特征图中重要区域的指导下有效地对标记之间的关系进行建模。这些聚焦区域由多组变形采样点确定，这些变形采样点是通过偏移网络从查询中学习到的。我们采用双线性插值从特征图中采样特征，然后将采样的特征馈送到键和值投影以获得变形的键和值。最后，应用标准的多头注意力来参与对采样键的查询并从变形值聚合特征。此外，变形点的位置提供了更强大的相对位置偏差，以促进可变形注意的学习，这将在以下部分中讨论。

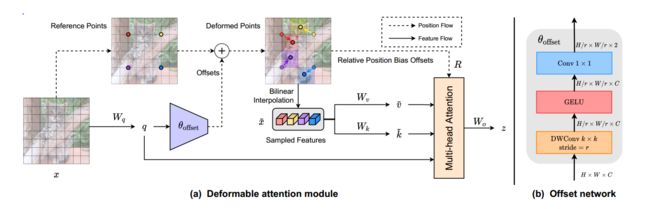
图 2. 可变形注意机制的图示。 (a) 呈现可变形注意力的信息流。在左侧部分，一组参考点均匀地放置在特征图上，其偏移量是通过偏移网络从查询中学习到的。然后根据变形点从采样的特征中投影出变形的键和值，如右图所示。相对位置偏差也由变形点计算，增强了输出变形特征的多头注意力。我们只展示了 4 个参考点以进行清晰的展示，实际实施中还有更多参考点。 (b) 揭示了偏移生成网络的详细结构，标有每一层的输入和输出特征图的大小。

可变形注意力模块。如图 2(a) 所示，给定输入特征图$x\in {\mathbb{R}}^{H\times W\times C}$，生成点$p\in {\mathbb{R}}^{H_G\times W_G\times 2}$的均匀网格作为参考。具体来说，网格尺寸从输入特征图尺寸下采样一个因子$r,H_G=H/r,W_G=$ $W/r$。参考点的值是线性间隔的二维坐标$\left\{(0,0),\dots ,\left(H_G-1,W_G-1\right)\right\}$，然后根据网格形状$H_G\times W_G$将它们归一化到范围$[-1,+1]$，其中$(-1,-1)$表示左上角和$(+1,+1)$表示右下角。为了获得每个参考点的偏移量，对特征图进行线性投影以获得查询标记$q=x{W}_q$，然后将其馈入轻量级子网络${\theta }_{\text{offset }}(\cdot )$以生成偏移量$\Delta p={\theta }_{\text{offset }}(q)$。为了稳定训练过程，我们通过一些预定义的因子$s$来缩放$\Delta p$的幅度，以防止偏移量变得太大，即$\Delta p\leftarrow s\tanh (\Delta p)$。然后在变形点的位置对特征进行采样作为键和值，然后是投影矩阵：
$$\begin{array}{rl}& q=x{W}_q,\tilde{k}=\tilde{x}{W}_k,\tilde{v}=\tilde{x}{W}_v,(6)\\ & \text{ with }\Delta p={\theta }_{\text{offset }}(q),\tilde{x}=\varphi (x;p+\Delta p).(7)\end{array}$$
$\tilde{k}$和$\tilde{v}$分别表示变形后的键和值嵌入。具体来说，我们将采样函数$\varphi (\cdot ;\cdot )$设置为双线性插值以使其可微分：
$$\varphi \left(z;\left(p_x,p_y\right)\right)=\sum _{\left(r_x,r_y\right)}g\left(p_x,r_x\right)g\left(p_y,r_y\right)z\left[r_y,r_x,:\right],(8)$$
其中$g(a,b)=\max (0,1-|a-b|)$和$\left(r_x,r_y\right)$索引$z\in {\mathbb{R}}^{H\times W\times C}$上的所有位置。由于$g$仅在最接近$\left(p_x,p_y\right)$的 4 个积分点上不为零，因此它将等式 (8) 简化为 4 个位置的加权平均值。与现有方法类似，我们对$q,k,v$执行多头注意力，并采用相对位置偏移$R$。注意力头的输出公式为：
$$z^{(m)}=\sigma \left(q^{(m)}{\tilde{k}}^{(m)\top }/\sqrt{d}+\varphi (\hat{B};R)\right){\tilde{v}}^{(m)},(9)$$
其中$\varphi (\hat{B};R)\in {\mathbb{R}}^{HW\times H_G{W}_G}$对应于先前工作 [23] 之后的位置嵌入，同时进行了一些改编。详细信息将在本节稍后说明。每个头部的特征连接在一起并通过$W_o$投影得到最终输出$z$，如等式（3）。

偏移生成。正如我们已经说过的，偏移量生成采用了一个子网络，它使用查询特征并分别输出参考点的偏移值。考虑到每个参考点覆盖一个局部$s\times s$区域（$s$是偏移量的最大值），生成网络也应该具有局部特征的感知，以学习合理的偏移量。因此，我们将子网络实现为两个具有非线性激活的卷积模块，如图 2(b) 所示。输入特征首先通过$5\times 5$深度卷积来捕获局部特征。然后，采用 GELU 激活和$1\times 1$卷积来获得 2D 偏移量。同样值得注意的是，$1\times 1$卷积中的偏差被降低以减轻所有位置的强制偏移。

偏移组。为了促进变形点的多样性，我们在 MHSA 中遵循类似的范例，并将特征通道分成 G 组。来自每个组的特征使用共享子网络分别生成相应的偏移量。在实践中，注意模块的头数 M 设置为偏移组 G 大小的倍数，以确保将多个注意头分配给一组变形的键和值。

可变形的相对位置偏差。相对位置偏差对每对查询和键之间的相对位置进行编码，从而通过空间信息增强普通注意力。考虑一个形状为$H\times W$的特征图，其相对坐标位移分别位于两个维度的$[-H,H]$和$[-W,W]$范围内。在 Swin Transformer [23] 中，构建了一个相对位置偏置表$\hat{B}\in {\mathbb{R}}^{(2H-1)\times (2W-1)}$，通过用两个方向的相对位移对表进行索引来获得相对位置偏置$B$。由于我们的可变形注意力具有连续的键位置，我们计算归一化范围$[-1,+1]$中的相对位移，然后在参数化偏差表中插值$\varphi (\hat{B};R)$通过连续的相对位移来覆盖所有可能的偏移值。

计算复杂性。可变形多头注意力 (DMHA) 与 PVT 或 Swin Transformer 中的对应物具有相似的计算成本。唯一的额外开销来自用于生成偏移量的子网络。整个模块的复杂度可以概括为：
$$\Omega (\text{ DMHA })=\underset{\text{vanilla self-attention module }}{2HW{N}_{\mathrm{s}}C+2HW{C}^2+2N_{\mathrm{s}}{C}^2}+\underset{\text{offset network }}{\left(k^2+2\right)N_{\mathrm{s}}C},$$
其中$N_{\mathrm{s}}=H_G{W}_G=HW/r^2$是采样点的数量。可以立即看出偏移网络的计算成本具有线性复杂度 w.r.t。通道大小，这相对于注意力计算的成本来说是较小的。通常，考虑用于图像分类的 Swin-T [23] 模型的第三阶段，其中$H=W=14,N_s=49,C=384$，单个块中注意模块的计算成本为 79.63M FLOPs。如果配备我们的可变形模块（$k=5$），额外开销为 5.08M Flops，仅占整个模块的 6.0%。此外，通过选择较大的下采样因子$r$，复杂度将进一步降低，这使其对具有更高输入分辨率的任务（例如目标检测和实例分割）更友好。