反光板导航SLAM（四）如何通过两个反光柱估计位姿

通常而言确定空间中的一个点的坐标需要三个点，也就是俗称的三点定位。但是在某些时候，场景内可能不一定能够采样到足够多的反光柱，比如只有两个。这个时候看起来似乎参数是不足的，毕竟机器人的参数有三个，两个方程是不够的，但是这个方程其实也不是没有解的方式，具体的解答方式继续往下看：

1、三点定位

对于要确认空间中机器人的位置，首先考虑一个情景：空间中已知有一个障碍物O1，现在根据激光数据测得机器人到A的距离为R1，则机器人可以处于以R1为半径的圆上的任意位置：

然后机器人再次看到了另外一个障碍物O2，且根据激光数据测得机器人到A的距离为R2，则机器人可以处于以R2为半径的圆上的任意位置，此时机器人的位置就有了两个约束，因此它不能出现在这两个圆上的任意位置了，为了满足条件：机器人位于圆1上又同时位于圆2上，所以它就必须得在两个圆的交点上，也就是图中的A点或者B点：

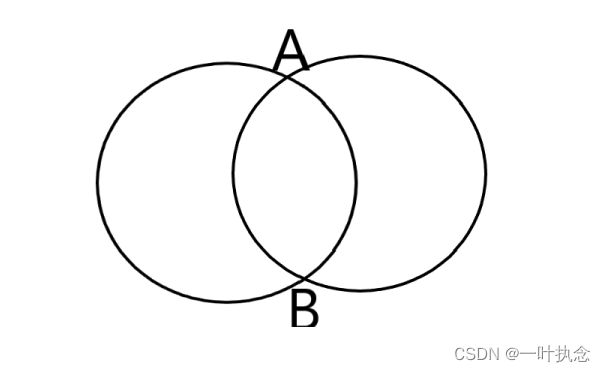
此时机器人的位置大致已经确定了，但是会存在双解的问题。但是如果现在机器人又看到了第三个障碍物,那么此时机器人的坐标就可以确定了：

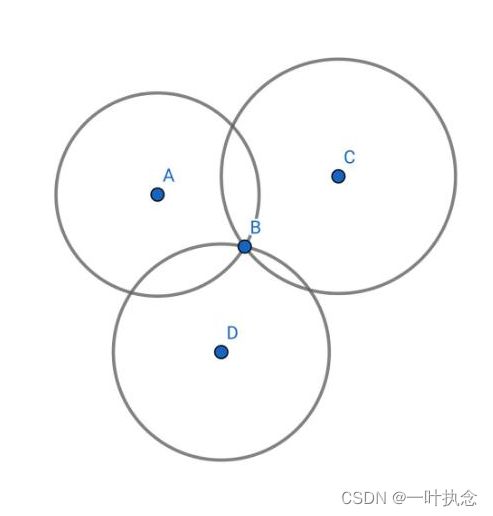
以上，就是简单的原理介绍。

那么根据上述理论来说，是不是说明整个定位过程中机器人的匹配点要一直保持着三个才可以保证定位呢，其实也不完全是的。其实两个点也是有可能确认出机器人的位姿的。

2、两点定位

前面我们提到了定位空间中的一个坐标需要三个点，但是同样注意到在只有两个观测目标的时候，机器人的位置是只有两种可能性的，这就为机器人确定位置提供了可能性。在已知匹配上两个点的反光柱的时候，机器人可能会存在于地图中的两个位置，但是这两个位置一般间隔还是比较远的，那么根据先验知识我们可以较为准确的判断出哪个点才是机器人实际存在的位置。具体思路如下：

2.1 匹配

匹配作为前置条件，假设我们当前获取到的反光柱点与实际地图上的反光柱点存在有且仅有两个点之间的匹配
$$\begin{gathered} [x1,y1,x2,y2] \\ [xw1,yw1,xw2,yw2] \end{gathered}$$

2.2 求角度

求角度的思路如下：
1、首先计算出两个匹配点之间的夹角theta,则该角度是为当前机器人的角度增量，但是它可能是正值也可能是负值，没有关系，先按正值考虑
2、将刚才的角度值回代到机器人，更新机器人的当前角度，重新计算当前帧下两个匹配点的坐标，因为机器人的角度变化了之前的值也就随之改变了。
3、重新计算两组匹配点之间的角度差，因为在第一步中我们计算出了当前机器人的一个角度增量，但是实际上它可能为正值也可能为负值，我们先按正值回代了，如果确实是正值那么目前机器人上两个点的连线方向与与之匹配的两个点的连线的夹角应该是趋于零的。如果变大了则说明刚才的赋值错误了，角度值应为负数。
4、更新角度，在第三步中确认角度增量的方向，然后更新最终的机器人朝向

2.3 求坐标

计算坐标：在上一步中我们知道了机器人的朝向，那么此时只剩下两个未知数，也就是机器人的坐标X、Y，则可以根据投影公式：

$$\begin{gathered} AW.x=cos(thetaR)\ast AR.x-sin(thetaR)\ast AR.y+XR \\ AW.y=sin(thetaR)\ast AR.x+cos(thetaR)\ast AR.y+YR \end{gathered}$$
来确定机器人的坐标(XR,YR)。

简单代码示例如下：

void Reflector::MatchToAngle(vector<pair<pair<double, double>, pair<double, double> > > &match_result,reflector_slam::RobotPose &robot_pose)
{
  double k1,k2,k3;
  double deta_angle;
  geometry_msgs::PointStamped point_robot1,point_robot2;
  pair<double, double> point1,point2;
  point1.first = match_result[0].first.first;
  point1.second = match_result[0].first.second;
  point2.first = match_result[1].first.first;
  point2.second = match_result[1].first.second;
  geometry_msgs::PointStamped point_world1,point_world2;
  reflector_slam::RobotPose old_pose;
  old_pose = last_pose;
  //获取两个点在世界坐标系下的坐标
  point_world1.point.x = point1.first*cos(old_pose.theta)-sin(old_pose.theta)*point1.second+old_pose.x;
  point_world1.point.y = point1.first*sin(old_pose.theta)+cos(old_pose.theta)*point1.second+old_pose.y;
  point_world2.point.x = point2.first*cos(old_pose.theta)-sin(old_pose.theta)*point2.second+old_pose.x;
  point_world2.point.y = point2.first*sin(old_pose.theta)+cos(old_pose.theta)*point2.second+old_pose.y;
  //cout<<"point_world1.x:"<
  //cout<<"point_world2.x:"<
  //cout<<"word_point1.x:"<
  //cout<<"word_point2.x:"<
  if((point_world1.point.x - point_world2.point.x)==0 || (match_result[0].second.first - match_result[1].second.first)==0)
  {
    ROS_INFO("can not calculate k1 or k2");
    return;
  }
  k1 = (point_world1.point.y - point_world2.point.y)/(point_world1.point.x - point_world2.point.x);
  k2 = (match_result[0].second.second - match_result[1].second.second)/(match_result[0].second.first - match_result[1].second.first);
  //cout<<"k1:"<
  deta_angle = atan(abs(k1-k2)/(1+k1*k2));
  //cout<<"deta_angle"<
  geometry_msgs::PointStamped point_world_new1,point_world_new2;
  point_world_new1.point.x = point1.first*cos(old_pose.theta+deta_angle)-sin(old_pose.theta+deta_angle)*point1.second+old_pose.x;
  point_world_new1.point.y = point1.first*sin(old_pose.theta+deta_angle)+cos(old_pose.theta+deta_angle)*point1.second+old_pose.y;
  point_world_new2.point.x = point2.first*cos(old_pose.theta+deta_angle)-sin(old_pose.theta+deta_angle)*point2.second+old_pose.x;
  point_world_new2.point.y = point2.first*sin(old_pose.theta+deta_angle)+cos(old_pose.theta+deta_angle)*point2.second+old_pose.y;
  //cout<<"point_world_new1.x:"<
  //cout<<"point_world_new2.x:"<
  if((point_world_new1.point.x - point_world_new2.point.x) == 0)
  {
    ROS_INFO("can not calculate k3");
    return;
  }
  k3 = (point_world_new1.point.y - point_world_new2.point.y)/(point_world_new1.point.x - point_world_new2.point.x);
  //cout<<"k3:"<
  //cout<<"old_theta:"<
  //斜率调整到基本一致，则应满足k2-k3趋向于零
  if(abs(k2-k1)>abs(k2-k3))
  {
    old_pose.theta += deta_angle;
  }
  else
    old_pose.theta -= deta_angle;
  //cout<<"new_theta:"<
  //cout<<"old_pose.x:"<
  //cout<<"old_pose.y:"<
  old_pose.x = match_result[0].second.first - cos(old_pose.theta)*match_result[0].first.first + sin(old_pose.theta)*match_result[0].first.second;
  old_pose.y = match_result[0].second.second - sin(old_pose.theta)*match_result[0].first.first - cos(old_pose.theta)*match_result[0].first.second;
  //cout<<"new_pose.x:"<
  //cout<<"new_pose.y:"<
  robot_pose = old_pose;
}