解决Hash（哈希表）冲突的四种方案

解决Hash（哈希）冲突的四种方案

参考&鸣谢

解决哈希冲突必须知道的几种方法 小僵鱼

你还应该知道的哈希冲突解决策略 vivo互联网技术

解决哈希冲突的三种方法 kaleidoscopic

每日一题(哈希表及哈希冲突解决办法) 和笙

一、Hash概述

哈希是一种通过对数据进行压缩, 从而提高效率的一种解决方法，但由于哈希函数有限，数据增大等缘故，哈希冲突成为数据有效压缩的一个难题。本文主要介绍哈希冲突、解决方案，以及各种哈希冲突的解决策略上的优缺点。

哈希冲突即不同key值产生相同的地址，即发生了hash冲突。一般来说，哈希冲突是无法避免的，所以就有了解决方案。

常见的解决Hash冲突的方案有开放寻址法、链地址法和再哈希法。

---

二、开放寻址法

原理是当发生hash冲突时，会以当前地址为基准，然后根据寻址方法（探查寻址），去寻找下一次地址。若依旧发生冲突，则继续寻址，直到找到一个空的位置为止。 通用的散列函数形式为：

Hi=（H（key）+di）% m （i=1，2，…，n）

其中H（key）为哈希函数，m 为表长，di称为增量序列。增量序列的取值方式不同，相应的再散列方式也不同。

线性探查

顺序查找表的下一个单元，直到找到一个空单元或查遍全表。

即当hash值为3冲突时(假设此时hash表长度为11)，利用线性探查的过程为：

H1 = (3+1)%11 = 4，此时若4依旧冲突，则再hash，即

H2 = (3+2)%11 = 5 … 通过这种线性增长增量系列，直到找到空的位置为止。

二次探查

这种方法的特点是，当哈希冲突时，在表的左右进行跳跃探测，比较灵活。

此时di = 1^2, -1^2, 2^2, -2^2 …

假设当hash值为3冲突时(假设此时hash表长度为11)，利用二次探查的过程为：

H1 = (3+1^2)%11 = 4,此时若4依旧冲突，则再hash,即

H2 = (3+(-1)^2)%11 = 2 …

通过该方法直到找到空位置为止。

伪随机探测

这种方法即是产生一些随机系列值，并给定随机数作为起点。

假设当hash值为3冲突时(假设此时hash表长度为11)，利用伪随机探测的过程为：

假设产生的随机系列为2，5，9 …，则

H1 = (3+2)%11 = 5

H2 = (3+5)%11 = 8

通过该方法直到找到空位置为止。

---

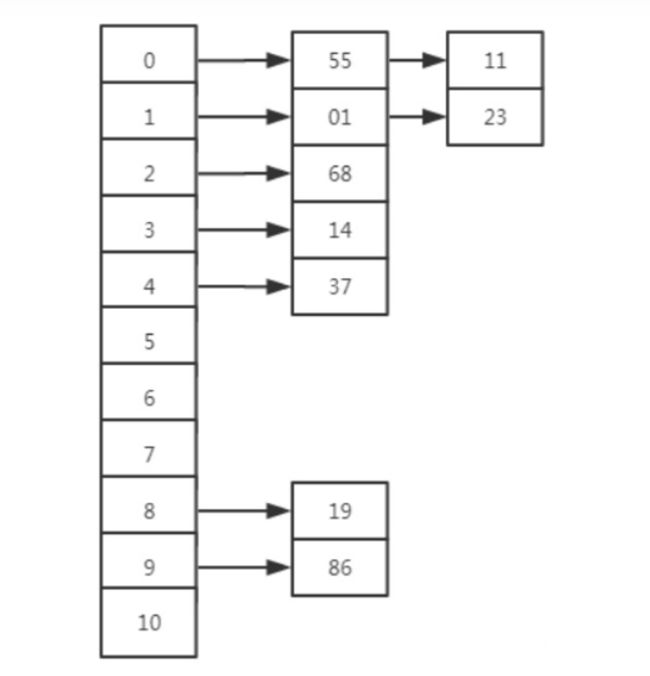
三、链地址法（拉链法）

HashMap，HashSet其实都是采用的拉链法来解决哈希冲突的，就是在每个位桶实现的时候，我们采用链表（jdk1.8之后采用链表+红黑树）的数据结构来去存取发生哈希冲突的输入域的关键字（也就是被哈希函数映射到同一个位桶上的关键字）。首先来看使用拉链法解决哈希冲突的几个操作：

• 插入操作：在发生哈希冲突的时候，我们输入域的关键字去映射到位桶（实际上是实现位桶的这个数据结构，链表或者红黑树）中去的时候，我们先检查带插入元素x是否出现在表中，很明显，这个查找所用的次数不会超过装载因子（n/m : n为输入域的关键字个数，m为位桶的数目），它是个常数，所以插入操作的最坏时间复杂度为O(1)的。
• 查询操作：和插入操作一样，在发生哈希冲突的时候，我们去检索的时间复杂度不会超过装载因子，也就是检索数据的时间复杂度也是O(1)的
• 删除操作：如果在拉链法中我们想要使用链表这种数据结构来实现位桶，在删除一个元素x的时候，需要更改x的前驱元素的next指针的属性，把x从链表中删除。这个操作的时间复杂度也是O(1)的。

与开放定址法相比，拉链法有如下几个优点：

①拉链法处理冲突简单，且无堆积现象，即非同义词决不会发生冲突，因此平均查找长度较短；

②由于拉链法中各链表上的结点空间是动态申请的，故它更适合于造表前无法确定表长的情况；

③开放定址法为减少冲突，要求装填因子α较小，故当结点规模较大时会浪费很多空间。而拉链法中可取α≥1，且结点较大时，拉链法中增加的指针域可忽略不计，因此节省空间；

④在用拉链法构造的散列表中，删除结点的操作易于实现。只要简单地删去链表上相应的结点即可。

拉链法的缺点

指针需要额外的空间，故当结点规模较小时，开放定址法较为节省空间，而若将节省的指针空间用来扩大散列表的规模，可使装填因子变小，这又减少了开放定址法中的冲突，从而提高平均查找速度。

---

四、再哈希法

fi=(f(key)+i*g(key)) % m (i=1，2，……，m-1)

其中，f(key) 和 g(key) 是两个不同的哈希函数，m为哈希表的长度

步骤：

双哈希函数探测法，先用第一个函数 f(key) 对关键码计算哈希地址，一旦产生地址冲突，再用第二个函数 g(key) 确定移动的步长因子，最后通过步长因子序列由探测函数寻找空的哈希地址。

比如，f(key)=a 时产生地址冲突，就计算g(key)=b，则探测的地址序列为 f1=(a+b) mod m，f2=(a+2b) mod m，……，fm-1=(a+(m-1)b) % m。

缺点：

每次冲突都要重新散列，计算时间增加。

---

五、公共溢出区法

即设立两个表：基础表和溢出表。将所有关键字通过哈希函数计算出相应的地址。然后将未发生冲突的关键字放入相应的基础表中，一旦发生冲突，就将其依次放入溢出表中即可。

在查找时，先用给定值通过哈希函数计算出相应的散列地址后，首先与基本表的相应位置进行比较，如果不相等，再到溢出表中顺序查找。