LeetCode——1237. 找出给定方程的正整数解

一、题目

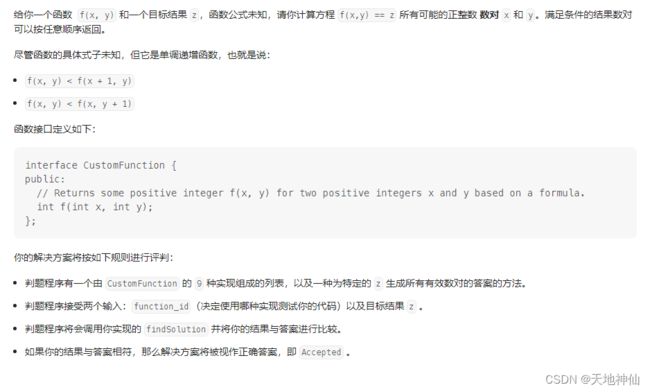
来源：力扣（LeetCode）
链接：https://leetcode.cn/problems/find-positive-integer-solution-for-a-given-equation/description/

翻译一下题目

意思是，这是一个二维单调递增的函数，函数一共有 9 种，我们可以直接调用 CustomFunction 这个类来使用他定义的函数。测试用例中输入的 function_id 不在我们的考虑范围内，这个 function_id 只是决定了他具体是采用了哪一种函数来进行运算。而我们要做的事情就是，找到所有满足函数等于 target 的数值对。另外建议出题人下次好好学学语文再来出题吧。

二、C++解法

我的思路及代码

枚举

因为他给出了数据的范围，所有我们可以枚举出所有的情况，然后和 target 进行比较，一样则加入答案。

class Solution {
public:
    vector<vector<int>> findSolution(CustomFunction& customfunction, int z) {
        vector<vector<int>> ans;
        for(int i=1;i<1000;i++){
            for(int j=1;j<1000;j++){
                if(z==customfunction.f(i,j)){
                    ans.push_back({i,j});
                }
            }
        }
        return ans;
    }
};

• 时间复杂度：O(mn)，其中 m 是 x 的取值数目，n 是 y 的取值数目
• 空间复杂度：O(1)

枚举改进

在枚举的基础上增加了提前退出循环的条件，由于该函数是单调递增，所以当 f(x,y) = target 时，f(x,y+1) > target 是一定的，所以我们可以减少很多不必要的循环。除此之外我们还可以进行改进，可以继续往下看

class Solution {
public:
    vector<vector<int>> findSolution(CustomFunction& customfunction, int z) {
        vector<vector<int>> ans;
        
        for(int i=1;i<1000;i++){
            for(int j=1;j<1000;j++){
                if(z==customfunction.f(i,j)){
                    ans.push_back({i,j});
                }
                if(z<customfunction.f(i,j))
                break;
            }
        }
        return ans;
    }
};

• 时间复杂度：O(mn)，其中 m 是 x 的取值数目，n 是 y 的取值数目
• 空间复杂度：O(1)

双指针

由于此函数单调递增，所以我们可以采用双指针，一个遍历 x 的从前往后遍历，另外一个遍历 y 的从后往前遍历，当遇到当前的函数值小于 target 时就说明此时在 x 不变的情况下，y 已经小了，所以我们将 x++ 然后还是从上次遍历停止的位置继续开始 y 的遍历。这样可以大幅度减少搜索的次数。

class Solution {
public:
    vector<vector<int>> findSolution(CustomFunction& customfunction, int z) {
        vector<vector<int>> ans;
        int j=1000;
        for(int i=1;i<1001;i++){ 
            for(;j>0;j--){
                if(z==customfunction.f(i,j))
                    ans.push_back({i,j});
                if(z>customfunction.f(i,j))
                    break;
            }
        }
        return ans;
    }
};

• 时间复杂度：O(m+n)，其中 m 是 x 的取值数目，n 是 y 的取值数目
• 空间复杂度：O(1)

官方参考代码

二分查找

题目本质是一个查找的题目，所以可以用二分查找的办法将时间复杂度降低到 nlogn 的级别

class Solution {
public:
    vector<vector<int>> findSolution(CustomFunction& customfunction, int z) {
        vector<vector<int>> res;
        for (int x = 1; x <= 1000; x++) {
            int yleft = 1, yright = 1000;
            while (yleft <= yright) {
                int ymiddle = (yleft + yright) / 2;
                if (customfunction.f(x, ymiddle) == z) {
                    res.push_back({x, ymiddle});
                    break;
                }
                if (customfunction.f(x, ymiddle) > z) {
                    yright = ymiddle - 1;
                } else {
                    yleft = ymiddle + 1;
                }
            }
        }
        return res;
    }
};

• 时间复杂度：O(mlog⁡n)，其中 m 是 x 的取值数目，n 是 y 的取值数目。
• 空间复杂度：O(1)